|
По первому тесту выполнил дважды задания. Результат получается правильный (проверял калькулятором). Пишет, что "Задание не проверено" и предлагает повторить. |
Графика в Lazarus
10.2 Построение графиков
Алгоритм построения графика непрерывной функции  на отрезке
на отрезке ![[a; b]](/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png) состоит в следующем: необходимо построить точки
состоит в следующем: необходимо построить точки 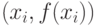 в декартовой системе координат и соединить их прямыми линиями. Координаты точек определяются по следующим формулам:
в декартовой системе координат и соединить их прямыми линиями. Координаты точек определяются по следующим формулам:
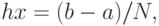
где  — количество отрезков на отрезке
— количество отрезков на отрезке ![[a; b]](/sites/default/files/tex_cache/65c152d51ed08a1761f5a8cb653eafe5.png) .
.
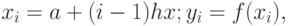
где 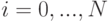 .
.
Чем больше точек будет изображено, тем более плавным будет построенный график.
При переносе этого алгоритма на форму или другой компонент Lazarus учитывает размеры и особенности компонента (ось ОX направлена слева направо, её координаты лежат в пределах от 0 до Width; ось OY направлена вниз, её координаты находятся в пределах от 0 до Height). Значения координат X и Y должны быть целыми.
Необходимо пересчитать все точки из "бумажной" системы координат ( изменяется в пределах от
изменяется в пределах от  до
до  ,
,  изменяется от минимального до максимального значения функции) в "
компонентную1Система координат, связанная с конкретным компонентом класса Tform, Timage, Tprinter и т. д." (в этой системе координат ось абсцисс обозначим буквой
изменяется от минимального до максимального значения функции) в "
компонентную1Система координат, связанная с конкретным компонентом класса Tform, Timage, Tprinter и т. д." (в этой системе координат ось абсцисс обозначим буквой  , а ось ординат — буквой
, а ось ординат — буквой  ).
).
Для преобразования координаты  в координату
в координату  построим линейную функцию
построим линейную функцию 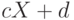 , которая переведёт точки из интервала
, которая переведёт точки из интервала 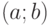 в точки интервала
в точки интервала  2
2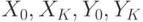 — отступы от левой, правой, нижней и верхней границы компонента Её решение позволит найти нам коэффициенты g и h.. Поскольку точка
— отступы от левой, правой, нижней и верхней границы компонента Её решение позволит найти нам коэффициенты g и h.. Поскольку точка  "бумажной" системы координат перейдет в точку
"бумажной" системы координат перейдет в точку 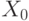 "экранной", а точка
"экранной", а точка  — в точку
— в точку 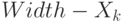 , то система линейных уравнений для нахождения коэффициентов
, то система линейных уравнений для нахождения коэффициентов  и
и  имеет вид:
имеет вид:
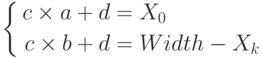
Решив её, найдём коэффициенты 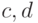 :
:

Для преобразования координаты  в координату
в координату  построим линейную функцию
построим линейную функцию  . Точка
. Точка  "бумажной" системы координат перейдет в точку
"бумажной" системы координат перейдет в точку 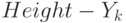 "компонентной", а точка
"компонентной", а точка 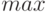 — в точку
— в точку 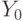 . Для нахождения коэффициентов
. Для нахождения коэффициентов  и
и  решим систему линейных алгебраических уравнений:
решим систему линейных алгебраических уравнений:
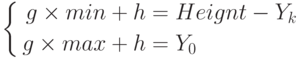
Её решение позволит найти нам коэффициенты  и
и  .
.

Перед описанием алгоритма построения графика давайте уточним формулы для расчёта коэффициентов 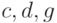 и
и  . Дело в том, что Width — это ширина компонента с учётом рамок слева и справа, а Height — полная высота компонента с учётом рамки, а если в качестве компонента будет использоваться форма, то необходимо учесть заголовок окна. Однако для изображения графика нам нужны вертикальные и горизонтальные размеры компонент без учёта рамок и заголовка. Эти размеры хранятся в свойствах ClientWidth (ширина клиентской области компонента без учёта ширины рамки) и ClientHeight (высота клиентской области компонента, без учёта ширины рамки и ширины заголовка) компонента. Поэтому для расчёта коэффициентов
. Дело в том, что Width — это ширина компонента с учётом рамок слева и справа, а Height — полная высота компонента с учётом рамки, а если в качестве компонента будет использоваться форма, то необходимо учесть заголовок окна. Однако для изображения графика нам нужны вертикальные и горизонтальные размеры компонент без учёта рамок и заголовка. Эти размеры хранятся в свойствах ClientWidth (ширина клиентской области компонента без учёта ширины рамки) и ClientHeight (высота клиентской области компонента, без учёта ширины рамки и ширины заголовка) компонента. Поэтому для расчёта коэффициентов 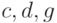 и
и  логичнее использовать следующие формулы:
логичнее использовать следующие формулы:
 |
( 10.2) |
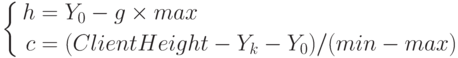 |
( 10.3) |
Алгоритм построения графика на экране монитора можно разделить на следующие этапы:
- Определить число отрезков
 , шаг изменения переменной
, шаг изменения переменной  .
. - Сформировать массивы
 , вычислить максимальное (max) и минимальное (min) значения
, вычислить максимальное (max) и минимальное (min) значения  .
. - Найти коэффициенты
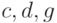 и
и  по формулам (10.1), (10.2).
по формулам (10.1), (10.2). - Создать массивы
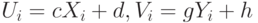 .
. - Последовательно соединить соседние точки прямыми линиями с помощью функции LineTo.
- Изобразить систему координат, линий сетки и подписи.
При построении графиков нескольких непрерывных функций вместо массивов  и
и  рационально использовать матрицы размером
рационально использовать матрицы размером  , где
, где  — количество функций. Элементы каждой строки матриц являются координатами соответствующего графика в "бумажной" (
— количество функций. Элементы каждой строки матриц являются координатами соответствующего графика в "бумажной" ( ) и "компонентной" (
) и "компонентной" ( ) системах координат.
) системах координат.
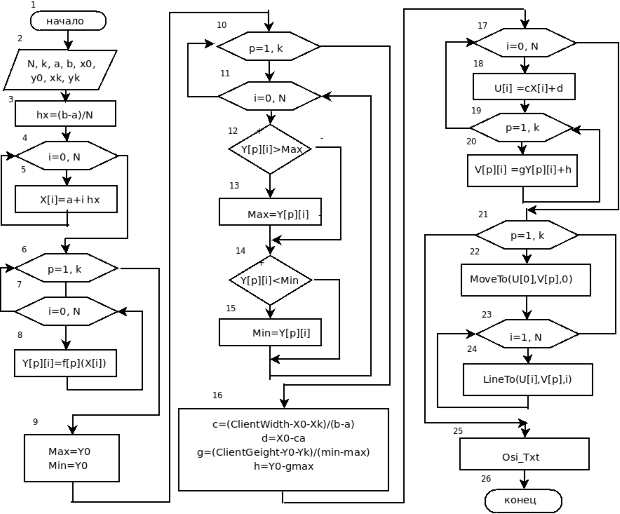
Блок-схема алгоритма изображения графика представлена на рис. 10.3, блок-схема построения графиков k непрерывных функций на рис. 10.4.
Рассмотрим поэтапно каждую схему.
Для рис. 10.3 первый этап алгоритма представлен в блоках 2 и 3. Второй этап реализуется в блоках 4—13. Коэффициенты третьего этапа рассчитываются в блоке 14. В блоках 15—16 формируются массивы значений  и
и  "компонентной системы координат (этап 4). Блоки 17—19 — это вывод графиков на экран, и блок 20 предназначен для шестого этапа.
"компонентной системы координат (этап 4). Блоки 17—19 — это вывод графиков на экран, и блок 20 предназначен для шестого этапа.
Для второй схемы (рис. 10.4) реализация второго этапа представлена в блоках 4—15. В блоке 16 рассчитываются коэффициенты 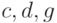 и
и  . В блоках 17—20 формируются массивы четвёртого этапа. Блоки 21—24 предназначены для вывода графиков, а блок 25 — для построения осей.
. В блоках 17—20 формируются массивы четвёртого этапа. Блоки 21—24 предназначены для вывода графиков, а блок 25 — для построения осей.
ЗАДАЧА 10.1. Построить график функции f (x) на интервале [a, b].Функция задана следующим образом:

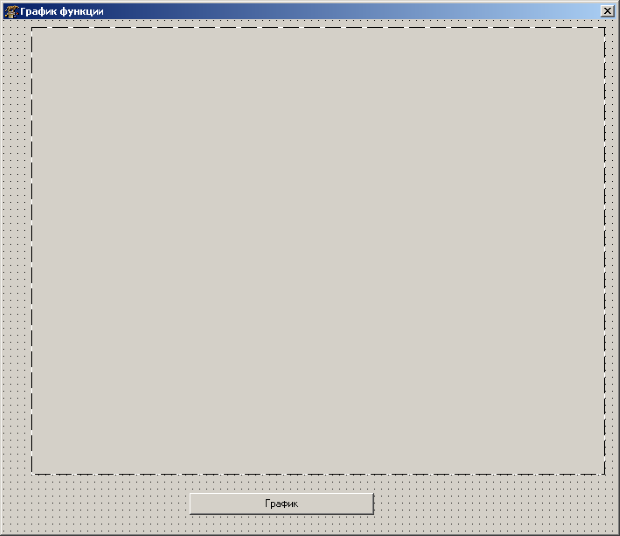
Создадим новый проект, изменим высоту и ширину формы до размеров, достаточных для отображения на ней графика. Например, можно установить следующие свойства: Width — 800, Height — 700. Разместим на форме кнопку и компонент класса TImage. Объект TImage1 — это растровая картинка, которая будет использоваться для отображения графика после щелчка по кнопке Button1. Размеры растровой картинки сделаем чуть меньше размеров формы.
Установим в качестве свойства формы Caption сроку "График функции".
Чтобы избавиться от проблемы перерисовки будущего графика при изменении размера формы, запретим изменение формы и уберём кнопки минимизации и максимизации окна. Свойство формы BorderStyle определяет внешний вид и поведение рамки вокруг окна формы. Для запрета изменения формы установим значение свойства BorderStyle в bsSingle — это значение определяет стандартную рамку вокруг формы и запрещает изменение размера формы. Чтобы убрать кнопки минимизации и максимизации формы, установим её свойства BolderIcons.BiMaximize и BolderIcons.BiMinimize в False.
Для кнопки установим свойство Caption — фразу "Построить график".
После установки всех описанных свойств окно формы должно стать подобным представленному на рис. 10.5.
Ввод интервала  и
и  выполним с помощью запроса в момент создания формы (в методе инициализации формы
выполним с помощью запроса в момент создания формы (в методе инициализации формы  ). Ниже приведён листинг модуля проекта рисования графика с комментариями:
). Ниже приведён листинг модуля проекта рисования графика с комментариями:
unit Unit1;
{$mode objfpc}{$H+}
interface
uses
Classes, SysUtils, LResources, Forms, Controls, Graphics,
Dialogs, ExtCtrls, StdCtrls;
//объявление функции, которая задаётся
//математически для построения
function f ( x : real ) : real;
//объявление функции, которая изображает
//график функции на компоненте
procedure Graphika ( a, b : real );
type
{ TForm1 }
TForm1 = class (TForm)
Button1 : TButton;
Image1 : TImage;
procedure Button1Click ( Sender : TObject );
procedure FormCreate ( Sender : TObject );
private
{ private declarations }
public
{ public declarations }
end;
var
Form1 : TForm1;
//объявление переменных
//x0, xk, y0, yk - отступы от границ компонента слева
//справа, сверху и снизу
//x, y - массивы, определяющие координаты точек графика
//в "бумажной" системе координат
//u, v массивы, определяющие координаты точек графика
//в "компонентной" системе координат
//N - количество точек
x0, y0, xk, yk, a, b : real;
x, y : array [ 0.. 1000 ] of real;
u, v : array [ 0.. 1000 ] of integer;
N : integer;
implementation
//функция, которая будет изображена на компоненте Image1
function f ( x : real ) : real;
begin
if x<=0 then Result := sin ( x /2)
else Result := sqrt ((1+x ) / 3 );
end;
//функция, которая рисует график
//заданной функции на компоненте Image1
procedure Graphika ( a, b : real );
//Kx+1 - количество линий сетки, перпендикулярных оси ОХ
//Ky+1 - количество линий сетки, перпендикулярных оси ОY
const Kx=5; Ky=5;
var
dx, dy, c, d, g, h, max, min : real;
i, tempx, tempy : integer;
s : string;
begin
//вычисление шага изменения по оси Х
h :=(b-a ) / (N-1);
//формирование массивов x и y
x [ 0 ] : = a;
y [ 0 ] : = f ( x [ 0 ] );
for i :=1 to N do
begin
x [ i ] : = x [ i - 1]+h;
y [ i ] : = f ( x [ i ] );
end;
//нахождение максимального и минимального значений массива Y
max:=y [ 0 ]; min:=y [ 0 ];
for i :=1 to N do
begin
if y [ i ]>max then max:=y [ i ];
if y [ i ]<min then min:=y [ i ];
end;
//формирование коэффициентов пересчёта из "бумажной" в
//"компонентную" систему координат
c :=(Form1. Image1. ClientWidth - x0-xk ) / ( b-a );
d:=x0-c * x [ 0 ];
g :=(Form1. Image1. ClientHeight -y0-yk ) / ( min- max );
h:=yk-g * max;
//формирование массивов точек в экранной системе координат
for i :=0 to N do
begin
u [ i ] : = trunc ( c * x [ i ]+d );
v [ i ] : = trunc ( g * y [ i ]+h );
end;
Form1. Image1. Canvas. Color := clGray;
Form1. Image1. Canvas. Pen. Mode:= pmNot;
//рисование графика функции на компоненте Image1
Form1. Image1. Canvas. MoveTo( u [ 0 ], v [ 0 ] );
Form1. Image1. Canvas. Pen. Width:= 2;
Form1. Image1. Canvas. Pen. Color := clGreen;
for i :=1 to N do
Form1. Image1. Canvas. LineTo ( u [ i ], v [ i ] );
Form1. Image1. Canvas. Pen. Width:= 1;
Form1. Image1. Canvas. Pen. Color := clBlack;
//рисование осей координат, если они попадают
//в область графика
Form1. Image1. Canvas. MoveTo( trunc ( x0 ), trunc ( h ) );
if ( trunc ( h)>yk ) and
( trunc ( h)< trunc ( Form1. Image1. ClientHeight - y0 ) )
then
Form1. Image1. Canvas. LineTo ( trunc ( Form1. Image1. ClientWidth
-xk ), trunc ( h ) );
Form1. Image1. Canvas. MoveTo( trunc ( d ), trunc ( yk ) );
if ( trunc ( d)>x0 ) and
( trunc ( d)< trunc ( Form1. Image1. ClientWidth -xk ) )
then
Form1. Image1. Canvas. LineTo ( trunc ( d ),
trunc ( Form1. Image1. ClientHeight - y0 ) );
//рисование линий сетки
//вычисление расстояния между линиями сетки в "компонентной" системе
//координат,перпендикулярными оси ОХ
dx :=(Form1. Image1. ClientWidth - x0-xk )/KX;
//выбираем тип линии для линий сетки
for i :=0 to KX do
begin
//первую и последнюю линии сетки рисуем обычной
//сплошной линией
if ( i =0) or ( i=KX) then
Form1. Image1. Canvas. Pen. Style := psSolid
//остальные рисуем пунктирными линиями
else
Form1. Image1. Canvas. Pen. Style := psDash;
//рисование линии сетки, перпендикулярной оси ОХ
Form1. Image1. Canvas. MoveTo( trunc ( x0+i * dx ), trunc ( yk ) );
Form1. Image1. Canvas. LineTo ( trunc ( x0+i * dx ),
trunc ( Form1. Image1. ClientHeight - y0 ) );
end;
//вычисление расстояния между линиями сетки в "компонентной" системе
//координат,перпендикулярными оси ОY
dy :=(Form1. Image1. ClientHeight -y0-yk )/KY;
for i :=0 to KY do
begin
//первую и последнюю линии сетки рисуем обычной сплошной линией
if ( i =0) or ( i=KY) then
Form1. Image1. Canvas. Pen. Style := psSolid
//остальные рисуем пунктирными линиями
else
Form1. Image1. Canvas. Pen. Style := psDash;
//рисование линии сетки, перпендикулярной оси ОY
Form1. Image1. Canvas. MoveTo( trunc ( x0 ), trunc ( yk+i * dy ) );
Form1. Image1. Canvas. LineTo ( trunc ( Form1. Image1. ClientWidth
-xk ), trunc ( yk+i * dy ) );
end;
Form1. Image1. Canvas. Pen. Style := psSolid;
//вывод подписей под осями
//определяем dx - расстояние между выводимыми
//под осью ОХ значениями
dx :=(b-a )/KX;
tempy:= trunc ( Form1. Image1. ClientHeight -y0 +10);
for i :=0 to KX do
begin
//преобразование выводимого значения в строку
Str ( a+i * dx : 5 : 2, s );
//вычисление х-координаты выводимого под осью ОХ значения
//в "компонентной" системе
tempx:= trunc ( x0+i * ( Form1. Image1. ClientWidth -x0-xk )/KX) -10;
//вывод значения под осью ОХ
Form1. Image1. Canvas. TextOut ( tempx, tempy, s );
end;
if ( trunc ( d)>x0 ) and ( trunc ( d)<Form1. Image1. ClientWidth -xk )
then
Form1. Image1. Canvas. TextOut ( trunc ( d) -5,tempy, ’ 0 ’ );
//определяем dy - расстояние между выводимыми левее
//оси ОY значениями
dy :=(max _min )/KY;
tempx : = 5;
for i :=0 to KY do
begin
//преобразование выводимого значения в строку
S t r (max -i * dy : 5 : 2, s );
//вычисление y-координаты выводимого левее оси ОY
//значения в "компонентной" системе
tempy:= trunc ( yk-5+i * ( Form1. Image1. ClientHeight
-y0-yk )/KY);
//вывод значения левее оси ОY
Form1. Image1. Canvas. TextOut ( tempx, tempy, s );
end;
if ( trunc ( h)>yk ) and
( trunc ( h)<Form1. Image1. ClientHeight -y0 )
then
Form1. Image1. Canvas. TextOut ( tempx+10, trunc ( h) -5, ’ 0 ’ );
tempx:= trunc ( x0+i * ( Form1. Image1. ClientWidth - x0-xk ) / 2 );
Form1. Image1. Canvas. TextOut ( tempx, 10, ’График функции ’ );
end;
{ TForm1 }
procedure TForm1. FormCreate ( Sender : TObject );
var s : string;
kod : integer;
begin
N:=100;
x0 := 40; xk := 40;
y0 := 40; yk := 40;
repeat
s := InputBox ( ’График непрерывной функции ’, ’Введите левую ’,
’границу ’, ’ -10 ’ );
Val ( s, a, kod );
until kod =0;
repeat
s := InputBox ( ’График непрерывной функции ’, ’Введите правую ’,
’границу ’, ’ 10 ’ );
Val ( s, b, kod );
until kod =0;
end;
procedure TForm1. Button1Click ( Sender : TObject );
begin
Graphika ( a, b );
end;
initialization
{$I unit1.lrs}
end.
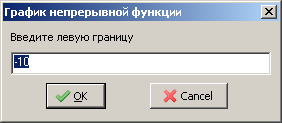
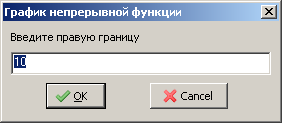
При запуске проекта появится запрос ввода левой (рисунок 10.6) и правой (рисунок 10.7) границ интервала.
После этого появится окно формы с кнопкой График. После щелчка по кнопке на форме прорисуется график функции (рис. 10.8).
Вместо заключения
Перевёрнута последняя страница книги. Что теперь? Авторы надеются, что знакомство с языком Free Pascal будет только первым этапом в изучении программирования. Желание читателя что-то исправить в книге: переписать приведённые в ней программы, предложить более простые и быстро работающие алгоритмы, написать свои программы и модули, будет лучшей благодарностью авторам. Если у Вас, читатель, появилось подобное желание, то мы выполнили свою задачу — научили Вас основам программирования.
Следующим этапом в освоении программирования будет разработка своих алгоритмов и написание реально работающих программ для различных операционных систем.
Мы надеемся, что это — только первая книга, посвящённая программированию. Думаем, что наша книга положит начало новой серии книг, посвящённой программированию в Linux. Следующей может стать книга, посвящённая решению более сложных задач на Free Pascal.