Слияние и сортировка слиянием

Реализации сортировки слиянием для связных списков

Раз уж для практической реализации сортировки слиянием все равно требуется дополнительная память, то можно рассмотреть и реализацию для связных списков. То есть вместо использования дополнительной памяти на вспомогательный массив можно применить ее для хранения ссылок. А кто-то может сразу столкнуться с проблемой сортировки связного списка (см. "Элементарные методы сортировки" ). Оказывается, сортировка слиянием очень удобна для связных списков. Полная реализация метода сортировки слиянием связных списков представлена в программе 8.6. Обратите внимание, что код самого слияния почти так же прост, как и для слияния массивов (программа 8.2).

Имея в своем распоряжении эту функцию слияния, легко получить рекурсивную нисходящую сортировку слиянием списков. Программа 8.7 является прямой рекурсивной реализацией функции, которая принимает в качестве параметра указатель на неупорядоченный список и возвращает указатель на список, содержащий те же элементы в отсортированном порядке. Эта программа выполняет свою работу, переупорядочивая узлы списка и не требуя создания ни временных узлов, ни вспомогательных списков. Для определения середины списка программа 8.7 использует хитрый прием; другие реализации могут передавать длину списка в рекурсивную программу либо в виде параметра, либо в самом списке. В силу рекурсивной формулировки эта программа проста для понимания, несмотря на достаточно сложный алгоритм.

Программа 8.6. Слияние связных списков

Данная программа сливает список, на который указывает a, со списком, на который указывает b, с помощью вспомогательного указателя с. Операция сравнения ключей в функции merge включает и равенство, так что слияние будет устойчивым, если по условию список b следует за списком a. Для простоты здесь принято, что все списки завершаются пустой ссылкой, но пригодны и другие соглашения относительно окончания списков (см. таблица 3.1). Что еще важнее, в коде не используются ведущие узлы списков, которых иначе было бы очень много.

link merge(link a, link b)
  { node dummy(0); link head = &dummy, c = head;
    while ((a != 0) && (b != 0))
      if ( a->item < b->item)
        { c->next = a; c = a; a = a->next; }
      else
      { c->next = b; c = b; b = b->next; }
    c->next = (a == 0) ? b : a;
    return head->next;
  }
        

Программа 8.7. Сортировка списков слиянием сверху вниз

Для выполнения сортировки эта программа разбивает список, на который указывает c, на две части, на которые указывают, соответственно, указатели a и b, рекурсивно сортирует эти части и получает окончательный результат с помощью функции merge (программа 8.6). Входной список должен заканчиваться пустой ссылкой (следовательно, так же должен заканчиваться и список b), а в конец списка a пустую ссылку заносит специальный оператор c->next = 0.

link mergesort(link c)
  { if (c == 0 || c->next == 0) return c;
    link a = c, b = c->next;
    while ((b != 0) && (b->next != 0))
      { c = c->next; b = b->next->next; }
    b = c->next; c->next = 0;
    return merge(mergesort(a), mergesort(b));
  }
        

К сортировке слиянием связных списков можно применить и восходящий подход " объединяй и властвуй " , хотя необходимость отслеживать ссылки делает его более сложным, чем кажется на первый взгляд. Как упоминалось при изучении нисходящих методов сортировки массивов в разделе 8.3, при разработке алгоритма восходящей сортировки слиянием списков не существует веских причин придерживаться точно того же набора слияний, что и для рекурсивной версии или версии, использующей массивы.

Сам собой напрашивается интересный вариант восходящей сортировки слиянием связных списков: помещаем элементы списка в циклический список, после чего проходим по списку, сливая пары упорядоченных подфайлов до полного завершения. Этот метод концептуально прост, однако (как это часто бывает в случае низкоуровневых программ обработки связных списков) его реализация может оказаться весьма запутанной (см. упражнение 8.36). Другой вариант восходящей сортировки слиянием связных списков, основанный на той же идее, представлен в программе 8.8: в нем все сортируемые списки хранятся в АТД очереди.

Программа 8.8. Восходящая сортировка слиянием связных списков

Данная программа реализует восходящую сортировку слиянием, используя АТД очереди (программа 4.18). Элементы очереди представляют собой упорядоченные связные списки. После инициализации очереди списками единичной длины программа просто извлекает из очереди два списка, сливает их и возвращает полученный результат в эту же очередь - и так до тех пор, пока не останется только один список. Этот способ, как и в случае восходящей сортировки слиянием, соответствует последовательности проходов по всем элементам, с удвоением на каждом проходе длины упорядоченных списков.

link mergesort(link t)
  { QUEUE<link> Q(max);
    if (t == 0 || t->next == 0) return t;
    for (link u = 0; t != 0; t = u)
      { u = t->next; t->next = 0; Q.put(t); }
    t = Q.get();
    while (!Q.empty())
      { Q.put(t); t = merge(Q.get(), Q.get()); }
    return t;
  }
        

Этот метод также концептуально прост, однако (как и для многих других высокоуровневых программ, использующих АТД) его реализация также может потребовать хитроумного программирования.

Одно из важных свойств этого метода заключается в том, что он использует упорядоченность, которая может присутствовать в файле. В самом деле, количество проходов по списку равно не 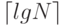, а , где S - количество упорядоченных подфайлов в исходном файле. Такой способ иногда называется естественной (natural) сортировкой слиянием. Для случайно упорядоченных файлов естественная сортировка слиянием не дает существенного выигрыша, разве что один-два прохода (фактически этот метод, видимо, будет медленнее нисходящего метода - из-за затрат на проверку упорядоченности файла), однако на практике достаточно часто встречаются файлы, состоящие из блоков упорядоченных подфайлов; и в таких ситуациях данный метод будет достаточно эффективен.

Упражнения

8.33. Разработайте реализацию нисходящей сортировки слиянием связных списков, которая передает рекурсивной процедуре длину списка в качестве параметра и использует ее для определения места разбиения списков.

8.34. Разработайте реализацию нисходящей сортировки слиянием для связных списков, которые содержат собственные длины в ведущих узлах, и использующей эти длины для определения места разбиения списков.

8.35. Добавьте в программу 8.7 отсечение небольших подфайлов. Определите предельный размер отсекаемых файлов, который ускоряет выполнение программы.

8.36. Реализуйте восходящую сортировку слиянием, использующую циклический связный список, как описано в тексте.

8.37. Добавьте в восходящую сортировку слиянием циклических списков из упражнения 8.36 отсечение небольших подфайлов. Определите предельный размер отсекаемых файлов, который ускоряет выполнение программы.

8.38. Добавьте в программу 8.8 отсечение небольших подфайлов. Определите предельный размер отсекаемых файлов, который ускоряет выполнение программы.

8.39. Нарисуйте дерево " объединяй и властвуй " , которое отображает слияния, выполняемые программой 8.8, для N = 16, 24, 31, 32, 33 и 39.

8.40. Нарисуйте дерево " объединяй и властвуй " , которое отображает слияния, выполняемые сортировкой слиянием циклического списка (упражнение 8.38), для N = 16, 24, 31, 32, 33 и 39.

8.41. Проведите эмпирические исследования, и на их основе выдвиньте гипотезу о количестве упорядоченных подфайлов в файле из N случайных 32-разрядных двоичных целых чисел.

8.42. Экспериментально определите количество проходов, необходимых для выполнения естественной сортировки слиянием случайных 64-разрядных двоичных ключей, при N = 10³, 10⁴, 10⁵ и 10⁶ . Подсказка: для выполнения этого упражнения не обязательно реализовать сортировку (и даже генерировать полные 64-разрядные ключи).

8.43. Преобразуйте программу 8.8 в программу естественной сортировки слиянием с помощью первоначального заполнения очереди упорядоченными подфайлами из входного файла.

8.44. Реализуйте естественную сортировку слиянием для массивов.

Возврат к рекурсии

Программы, представленные в данной главе, и быстрая сортировка, рассмотренная в предыдущей главе - это типичные реализации алгоритмов " разделяй и властвуй " . В последующих главах мы ознакомимся с еще несколькими алгоритмами подобной структуры, так что стоит более подробно рассмотреть основные характеристики этих реализаций.

Возможно, быструю сортировку было бы точнее назвать алгоритмом " властвуй и разделяй " : в рекурсивных реализациях при каждом обращении большая часть работы выполняется перед рекурсивными вызовами. А вот рекурсивная сортировка слиянием более соответствует принципу " разделяй и властвуй " : вначале файл делится на две части, и затем каждая часть обрабатывается отдельно. Сортировка слиянием сначала выполняется для небольших задач, а в заключение обрабатывается самый большой подфайл. Быстрая сортировка начинается с обработки наибольшего подфайла и завершается обработкой подфайлов небольших размеров. Любопытно сравнение этих алгоритмов по аналогии с управлением коллективом сотрудников, упомянутой в начале данной главы: быстрая сортировка соответствует тому, что каждый руководитель затрачивает свои усилия на правильное разбиение задачи на подзадачи, так что после выполнения всех подзадач работа будет успешно выполнена; сортировка слиянием соответствует тому, что каждый руководитель быстро и произвольно делит задачу пополам, а затем, после решения подзадач, затрачивает свои усилия на объединение результатов.

Это различие ясно видно в нерекурсивных реализациях. Быстрой сортировке нужен стек - для хранения больших подзадач, разбиение на которые зависит от входных данных. Сортировка слиянием допускает простые нерекурсивные реализации, поскольку способ разбиения файла на части не зависит от данных, и становится возможным изменение очередности решения подзадач, что позволяет упростить программу.

Существует точка зрения, что быструю сортировку естественнее рассматривать как нисходящий алгоритм, поскольку он начинает работу на вершине дерева рекурсии, а затем для завершения сортировки опускается вниз. Можно обдумать и нерекурсивный вариант быстрой сортировки, которая обходит дерево рекурсии сверху вниз, но по уровням. Таким образом, сортировка многократно проходит по массиву, разбивая файлы на меньшие подфайлы. Для массивов этот метод не годится из-за большого объема затрат на хранение информации о подфайлах, а для связных списков он аналогичен восходящей сортировке слиянием.

Сортировка слиянием и быстрая сортировка отличаются по признаку устойчивости. Если подфайлы при сортировке слиянием упорядочены с соблюдением устойчивости, то вполне достаточно обеспечить устойчивость слияния, что сделать совсем нетрудно. Рекурсивная структура алгоритма автоматически приводит к индуктивному доказательству устойчивости. Но для реализации быстрой сортировки с использованием массивов нет очевидного простого способа разбиения файлов, обеспечивающего устойчивость, так что устойчивость исключается еще до вступления в дело рекурсии. Хотя примитивная реализация быстрой сортировки для связных списков является устойчивой (см. упражнение 7.4).

Как было показано в "Рекурсия и деревья" , алгоритмы с одним рекурсивным вызовом могут быть сведены к циклу, но алгоритмы с двумя рекурсивными циклами, наподобие сортировки слиянием или быстрой сортировки, открывают дверь в мир алгоритмов вида " разделяй и властвуй " и древовидных структур, к которому принадлежат и наши лучшие алгоритмы. Сортировка слиянием и быстрая сортировка заслуживают тщательного изучения не только из-за их важного практического значения, но и потому, что они позволяют лучше уяснить сущность рекурсии для разработки и понимания других рекурсивных алгоритмов.

Упражнения

8.45. Допустим, сортировка слиянием реализована таким образом, что разбиение файла выполняется в произвольном месте, а не точно в середине файла. Сколько в среднем сравнений выполнит этот метод для упорядочения N элементов?

8.46. Проведите анализ эффективности сортировки слиянием при упорядочении строк. Сколько в среднем сравнений символов выполняется при сортировке большого файла?

8.47. Проведите эмпирические исследования по сравнению производительности быстрой сортировки связных списков (см. упражнение 7.4) и нисходящей сортировки слиянием связных списков (программа 8.7).