НОУ ИНТУИТ | Введение в Octave. Лекция 12: Обработка результатов эксперимента. Интерполяция функций

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 12.03.2015 | Уровень: для всех | Доступ: платный | ВУЗ: Компания ALT Linux

|

Вам нравится? Нравится 15 студентам

| Поделиться |

Поддержать программу

12.1.2 Полином Ньютона

И. Ньютон предложил интерполирующую функцию записать в виде следующего полинома -й степени:

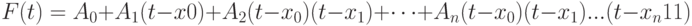$F(t)=A_0+A_1(t-x0)+A_2(t-x_0)(t-x_1)+\cdots+A_n(t-x_0)(t-x_1)...(t-x_n11)$

( 12.5)

Таблица 12.1. Таблица разделённых разностей полинома Ньютона
x	f(x)	1	2	3	4	...	n

		$y_{01}$
		$y_{01}$	$y_{02}$	$y_{012}$
		$y_{03}$	$y_{013}$	$y_{0123}$
		$y_{04}$	$y_{014}$	$y_{0124}$	$y_{01234}$
...	...	...	...	...	...	...	...
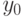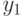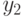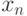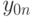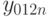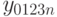		$y_{0n}$	$y_{01n}$	$y_{012n}$	$y_{0123n}$	...	$y_{012...n}$

Подставим 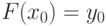F(x_0)=y_0 в (12.5) и вычислим значение коэффициента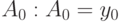 A_0:A_0=y_0

Подставим 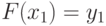F(x_1)=y_1 1) в (12.5), после чего получим соотношение для вычисления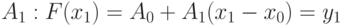 A_1:F(x_1)=A_0+A_1(x_1-x_0)=y_1

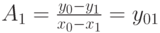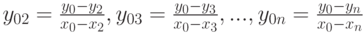
Отсюда коэффициент A_1 рассчитывается по формуле: $A_1=\frac{y_0-y_1}{x_0-x_1}=y_{01}$ , где $y_{01}$ — разделённая разность первого порядка, которая стремится к первой производной функции при $x_1\to x_0$ . По аналогии вводятся и другие разделённые разности первого порядка: $y_{02}=\frac{y_0-y_2}{x_0-x_2},y_{03}=\frac{y_0-y_3}{x_0-x_3},...,y_{0n}=\frac{y_0-y_n}{x_0-x_n}$

Подставим соотношение 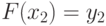F(x_2)=y_2 в (12.5), в результате чего получим:

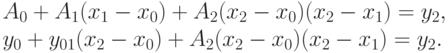
$A_0+A_1(x_1-x_0)+A_2(x_2-x_0)(x_2-x_1)=y_2,\\y_0+y_{01}(x_2-x_0)+A_2(x_2-x_0)(x_2-x_1)=y_2.$

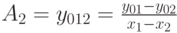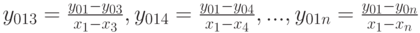Отсюда A_2 вычисляется по формуле $A_2=y_{012}=\frac{y_{01}-y_{02}}{x_1-x_2}$ , здесь $y_{012}$ — разделённая разность второго порядка, эта величина стремится ко второй производной при $x_1\to x_2$ . Аналогично вводятся $y_{013}=\frac{y_{01}-y_{03}}{x_1-x_3},y_{014}=\frac{y_{01}-y_{04}}{x_1-x_4},...,y_{01n}=\frac{y_{01}-y_{0n}}{x_1-x_n}$ .

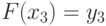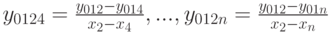Подставим F(x_3)=y_3 в (12.5), после чего получим $A_3=y_{0123}=\frac{y_{012}-y_{013}}{x_2-x_3}$ . Аналогично можно ввести коэффициенты $y_{0124}=\frac{y_{012}-y_{014}}{x_2-x_4},...,y_{012n}=\frac{y_{012}-y_{01n}}{x_2-x_n}$ .

Этот процесс будем продолжать до тех пор, пока не вычислим 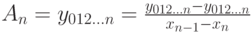$A_n=y_{012...n}=\frac{y_{012...n}-y_{012...n}}{x_{n-1}-x_n}$ .

Полученные результаты запишем в табл. 12.1

В вычислении по формуле (12.5) будут участвовать только диагональные элементы таблицы (т.е. коэффициенты A_i ), а все остальные элементы таблицы являются промежуточными и нужны для вычисления диагональных элементов.

Дальше >>

Введение в Octave

Введение в Octave

Обработка результатов эксперимента. Интерполяция функций

12.1.2 Полином Ньютона

Вопросы и ответы

Студенты

Авторизоваться

Введение в Octave

Введение в Octave

Обработка результатов эксперимента. Интерполяция функций

12.1.2 Полином Ньютона

Вопросы и ответы

Студенты