НОУ ИНТУИТ | Введение в Octave. Лекция 10: Решение оптимизационных задач

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 12.03.2015 | Уровень: для всех | Доступ: платный | ВУЗ: Компания ALT Linux

|

Вам нравится? Нравится 14 студентам

| Поделиться |

Поддержать программу

Пример 10.6. Найти такие значения переменных $x_{1},x_{2},x_{3},x_{4}$ при которых функция цели $L=-x_{2}-2x_{3}+4x_{4}$ достигает своего минимального значения и удовлетворяются ограничения:

$\left\{\begin{aligned} 3x_{1}&-x_{2}\le 2\\ x_{2}&-2x_{3}\le -1\\ 4x_{3}&-x_{4}\le 3\\ 5x_{1}&+x_{4}\ge 6\\ x_{1}&\ge 0,\ x_{2}\ge0,\ x_{3}\ge 0,\ x_{4}\ge 0. \end{aligned}\right.$

Сформируем параметры функции gplk

$c=\begin{pmatrix}0\\-1\\-2\\4\end{pmatrix}$ — коэффициенты при неизвестных функции цели,

$a=\begin{pmatrix}3&-1&0&0\\0&1&-2&0\\0&0&4&-1\\5&0&0&1\end{pmatrix}$ — матрица системы ограничений,

$b=\begin{pmatrix}2\\-1\\3\\6\end{pmatrix}$ –– свободные члены системы ограничений,

ctype ="UUUL" — массив, определяющий тип ограничения^{4Первые три ограничения типа "меньше", четвёртое — типа "больше"},

vartype ="CCCC" — массив, определяющий тип переменной, в данном случае все переменные вещественные,

sense = 1 –– задача на минимум.

Текст программы решения задачи приведён в листинге 10.8.

	
c = [0; -1; -2; 4]; a =[3 -1 0 0; 0 1 -2 0; 0 0 4 -1;5 0 0 1];
b = [2; -1; 3; 6];
ctype="UUUL"; vartype= "CCCC"; sense =1;
[xmin, fmin, status] =glpk(c, a, b, [0; 0; 0; 0], [], ctype, vartype, sense)
% Результаты решения
xmin =
	1.00000
	1.00000
	1.00000
	1.00000
fmin = 1.00000
status = 180

Листинг 10.8. Решение задачи из примера 10.6

Минимальное значение L = 1 достигается при $x=\begin{pmatrix}1\\1\\1\\1\end{pmatrix}$ . Значение переменной status равно 180, что свидетельствует о корректном решении задачи линейного программирования.

Пример 10.7. Найти такие значения переменных $x_{1},x_{2},x_{3}$ при которых функция цели $L=-5+x_{1}-x_{2}-3x_{3}$ достигает своего минимального значения и удовлетворяются ограничения:

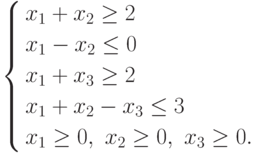
$\left\{ \begin{aligned} x_{1}&+x_{2}\ge 2\\ x_{1}&-x_{2}\le 0\\ x_{1}&+x_{3}\ge 2\\ x_{1}&+x_{2}-x_{3}\le 3\\ x_{1}&\ge 0,\ x_{2}\ge 0,\ x_{3}\ge 0. \end{aligned} \right.$

Сформируем параметры функции gplk :

$c=\begin{pmatrix}1\\-1\\-3\end{pmatrix}$ — коэффициенты при неизвестных функции цели,

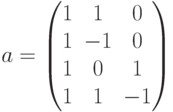$a=\begin{pmatrix}1&1&0\\1&-1&0\\1&0&1\\1&1&-1\end{pmatrix}$ — матрица системы ограничений (три переменных и четыре ограничения),

$b=\begin{pmatrix}2\\0\\2\\3\end{pmatrix}$ — свободные члены системы ограничений,

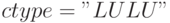ctype ="LULU" — массив символов, определяющий тип ограничения^{5Первое и третье ограничения типа "больше", второе четвёртое — типа "меньше".},

vartype ="CCC" — массив, определяющий тип переменной, в данном случае все переменные вещественные,

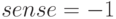sense = -1 –– задача на максимум.

Текст программы решения задачи приведён в листинге 10.9.

	
c =[1; -1; -3]; a =[1 1 0; 1 -1 0; 1 0 1; 1 1 -1]; b = [2; 0; 2; 3];
ctype="LULU"; vartype= "CCC"; sense =-1;
[xmax, fmax, status]= glpk(c, a, b, [ ], [ ], ctype, vartype, sense)
% Результаты решения
xmax =
	1.66667
	1.66667
	0.33333
fmax = -1.0000
status = 180

Листинг 10.9. Решение задачи из примера 10.7

Минимальное значение^{6Авторы обращают внимание читателей в Octave было равно -1, а потом к нему необходимо было прибавить -5} L = -6 достигается при $x=\begin{pmatrix}1.66667\\1.66667\\0.33333\end{pmatrix}$

Значение переменной 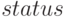status равно 180, что свидетельствует о корректном решении задачи линейного программирования.

Решим задачу 10.7, как задачу целочисленного программирования (см. листинг 10.10)

	
c =[1; -1; -3]; a =[1 1 0; 1 -1 0; 1 0 1; 1 1 -1]; b = [2; 0; 2; 3];
ctype="LULU"; vartype= "III"; sense =-1;
[xmax, fmax, status]= glpk(c, a, b, [ ], [ ], ctype, vartype, sense)
% Результаты решения
xmin =
	2
	2
	1
fmin = -3
status = 171

Листинг 10.10. Решение задачи из примера 10.7 в целых числах

Значение 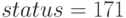status = 171 свидетельствует о корректном решении задачи целочисленного программирования, значение L = -8 достигается при $x=\begin{pmatrix}2\\2\\1\end{pmatrix}$

Дальше >>

Введение в Octave

Введение в Octave

Решение оптимизационных задач

Вопросы и ответы

Студенты

Авторизоваться

Введение в Octave

Введение в Octave

Решение оптимизационных задач

Вопросы и ответы

Студенты