|
Возможна ли разработка приложения на Octave с GUI? |
Нелинейные уравнения и системы
7.2 Решение трансцендентных уравнений
Уравнение, в котором неизвестное входит в аргумент трансцендентных функций, называется трансцендентным уравнением. К трансцендентным уравнениям принадлежат показательные, логарифмические, тригонометрические.
Для решения трансцендентных уравнений вида 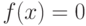 в Octave существует функция
в Octave существует функция  или
или ![fzero(name, [a, b])](/sites/default/files/tex_cache/5fff2a3e9373b95b078fec50acd24f67.png) , где
, где 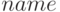 — имя функции, вычисляющей левую часть уравнения,
— имя функции, вычисляющей левую часть уравнения, 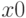 — начальное приближение к корню,
— начальное приближение к корню, ![[a, b]](/sites/default/files/tex_cache/022022f289db140169cd9514f74ee648.png) — интервал изоляции корня.
— интервал изоляции корня.
Если функция вызывается в формате: ![[x, y] = fzero(name, x0)](/sites/default/files/tex_cache/2562efaafed3bb64258ee94f5d6ac5c0.png) , то здесь
, то здесь  — корень уравнения,
— корень уравнения,  — значение функции в точке
— значение функции в точке  .
.
Пример 7.14. Найти решение уравнения:
![\sqrt[3]{(2x-3)^2}- \sqrt[3]{(x-1)^2}=0.](/sites/default/files/tex_cache/2797184839ebd07b7f8e224ba3830f7f.png)
Начнём решение данного трансцендентного уравнения с определения интервала изоляции корня. Воспользуемся для этого графическим методом. Построим график функции, указанной в левой части уравнения (листинг 7.15), создав предварительно функцию для её определения.
% Функция для вычисления левой части уравнения f(x)=0
function y=f1(x)
y=((2-x-3).^2).^(1/3)-((x-1).^2).^(1/3);
end;
% Построение графика функции f(x)
cla; okno1=figure();
x = -1:0.1:3;
y=f1(x);
pol=plot(x, y);
set(pol, ’LineWidth’, 3, ’Color’, ’k’)
set(gca, ’xlim’, [-1, 3]); set(gca, ’ylim’, [-1,1.5]);
set(gca, ’xtick’, [-1:0.5:3]); set(gca, ’ytick’,[-1:0.5:1.5]);
grid on; xlabel(’x’); ylabel(’y’);
title(’Plot y=(2x-3)^{2/3}-(x-1)^{2/3}’);
Листинг
7.15.
Графическое отделение корней (пример 7.14).
На графике (рис. 7.3) видно, что функция  дважды пересекает ось
дважды пересекает ось 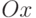 . Первый раз на интервале [1, 1.5], второй — [1.5, 2.5].
. Первый раз на интервале [1, 1.5], второй — [1.5, 2.5].
Уточним корни, полученные графическим методом. Воспользуемся функцией, вычисляющей левую часть заданного уравнения из листинга 7.15 и обратимся к функции  , указав в качестве параметров имя созданной функции и число (1.5) близкое к первому корню:
, указав в качестве параметров имя созданной функции и число (1.5) близкое к первому корню:
>>> x1=fzero(’f1’, 1.5) x1 = 1.3333
Теперь применим функцию  , указав в качестве параметров имя функции, и интервал изоляции второго корня:
, указав в качестве параметров имя функции, и интервал изоляции второго корня:
>>> x2=fzero(’f1’, [1.52.5]) x1= 2
Не трудно заметить, что и в первом и во втором случае функция  правильно нашла корни заданного уравнения.
правильно нашла корни заданного уравнения.
Ниже приведён пример некорректного обращения к функции  , здесь интервал изоляции корня задан неверно. На графике видно, что на концах этого интервала функция знак не меняет, или, другими словами, выбранный интервал содержит сразу два корня.
, здесь интервал изоляции корня задан неверно. На графике видно, что на концах этого интервала функция знак не меняет, или, другими словами, выбранный интервал содержит сразу два корня.
>>>fzero(’f1’, [1 3]) error: fzero: not a valid initial bracketing error: called from: error: /usr/share/octave/3.4.0/m/optimization/fzero.m at line 170, column 5
В следующем листинге приведён пример обращения к функции  в полном формате:
в полном формате:
>>> [X(1),Y(1)]= fzero(’f1’, [1 1.5]); >>> [X(2),Y(2) ]= fzero(’f1’, [1.5 2.5]); >>> X % Решение уравнения X = 1.3333 2.0000 >>> Y % Значения функции в точке Х Y = -2.3870e-15 0.0000e+00
Пример 7.15. Найти решение уравнения 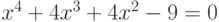 .
.
Как видим, левая часть уравнения представляет собой полином. В примере 7.13 было показано, что данное уравнение имеет четыре корня: два действительных и два мнимых (листинг 7.14).
Листинг 7.16 демонстрирует решение алгебраического уравнения при помощи функции  . Не трудно заметить, что результатом работы функции являются только действительные корни. Графическое решение (рис. 7.2) подтверждает это: функция дважды пересекает ось абсцисс.
. Не трудно заметить, что результатом работы функции являются только действительные корни. Графическое решение (рис. 7.2) подтверждает это: функция дважды пересекает ось абсцисс.
function y=f2(x) y=x.^4+4-x.^3+4-x.^2-9; end; >>> [X(1),Y(1)]= fzero(’f2’, [-4 -2]); >>> [X(2),Y(2)]= fzero(’f2’, [0 2]); >>> X >>> Y X = -3 1 Y = 0 0Листинг 7.16. Решение уравнения с помощью fzero (пример 7.15).

