| Россия, Липецк |
Опубликован: 11.10.2012 | Уровень: специалист | Доступ: платный
Самостоятельная работа 8:
Оптимизация и распараллеливание вычислительной программы на примере моделирования системы взаимодействующих частиц методом молекулярной динамики
Пример 1
Далее приводится листинг программы молекулярной динамики.
program mol_dyn
implicit real(8) (a-h, o-z)
integer, parameter :: ndim = 1000
!
! Массивы координат, проекций скоростей и ускорений частиц
!
real(8), dimension(1:ndim) :: x, y, vx, vy, ax, ay
!
! Задание начальной конфигурации частиц
!
call start(x, y, vx, vy, N, Sx, Sy, dt, dt2, nsnap, ntime)
!
! Вычисление ускорений частиц
!
call accel(x, y, ax, ay, N, Sx, Sy, zpe)
zpe =0.0d0
!
! Энергия выводится через nsnap шагов
!
do isnap = 1, nsnap
!
! Внутренний цикл - по шагам по времени
!
do itime = 1, ntime
!
! Выполняется сдвиг частиц
!
call move(x, y, vx, vy, ax, ay, N, Sx, Sy, dt, dt2, zke, zpe)
end do
!
! Вывод значений энергии: кинетической, потенциальной и полной
!
call output(zke, zpe, Sx, Sy, dt, N, ntime)
end do
end program
!
!====================================================
!
subroutine start(x, y, vx, VY, N, Sx, Sy, dt, dt2, nsnap, ntime)
implicit real(8) (a-h, o-z)
integer, parameter :: ndim = 1000
real(8), dimension(1:ndim) :: x, y, vx, vy, ax, ay
!
! Число частиц
!
n = 200
!
! Размер области моделирования
!
sx = 100.0d0
sy = 100.0d0
!
! Шаг по времени
!
dt = 1.0d-11
dt2 = dt**2
!
! Максимальное значение скорости
!
vmax = 10.0d0
!
! Число строк в таблице вывода и количество шагов по времени
между ними
!
nsnap = 200
ntime = 500
!
! Формируется начальная хаотическая конфигурация
!
do i = 1, N
call rndm(ranx)
x(i) = sx * ranx
call rndm(rany)
y(i) = sy * rany
call rndm(ranx)
call rndm(rany)
vx(i) = vmax * (2 * ranx - 1)
vy(i) = vmax * (2 * rany - 1)
end do
do i = 1, N
vxcum = vxcum + vx(i)
vycum = vycum + vy(i)
end do
vxcum = vxcum / N
vycum = vycum / N
do i = 1, N
vx(i) = vx(i) - vxcum
vy(i) = vy(i) - vycum
end do
end subroutine
!
!====================================================
!
subroutine move(x, y, vx, vy, ax, ay, N, Sx, Sy, dt, dt2, zke, zpe)
implicit real(8) (a-h, o-z)
integer, parameter :: ndim = 1000
real(8), dimension(1:ndim) :: x, y, vx, vy, ax, ay
do i = 1, N
xnew = x(i) + vx(i) * dt + 0.5d0 * ax(i) * dt2
ynew = y(i) + vy(i) * dt + 0.5d0 * ay(i) * dt2
!
! Учет периодических граничных условий
!
call cellp(xnew, ynew, vx(i), vy(i), sx, sy)
x(i) = xnew
y(i) = ynew
vx(i) = vx(i) + 0.5d0 * ax(i) * dt
vy(i) = vy(i) + 0.5d0 * ay(i) * dt
end do
call accel(x, y, ax, ay, N, Sx, Sy, zpe)
do i = 1, n
vx(i) = vx(i) + 0.5d0 * dt * ax(i)
vy(i) = vy(i) + 0.5d0 * dt * ay(i)
zke = zke + vx(i)**2 + vy(i)**2
end do
end subroutine
!
!====================================================
!
subroutine accel(x, Y, ax, ay, N, sx, sy, zpe)
implicit real(8) (a-h, o-z)
integer, parameter :: ndim = 1000
real(8), dimension(1:ndim) :: x, y, ax, ay
do i = 1, n
ax(i) = 0.0d0
ay(i) = 0.0d0
end do
do i = 1, n
do j = 1, n
if(i /= j) then
dx = x(i) - x(j)
dY = y(i) - y(j)
if(dabs(dx) > 0.5 * sx) dx = dx - sign(sx, dx)
if(dabs(dy) > 0.5 * sy) dy = dy - sign(sy, dy)
!
! Вычисление силы, действующей на j-ю частицу
!
r = dsqrt(dx**2 + dy**2)
ri = 1.0d0 / r
ri6 = ri**6
g = 24.0d0 * ri6 * ri * (2.0d0 * ri6 - 1)
force = 0.5d0 * g * ri
pot = 4.0d0 * ri6 * (ri6**2 - 1.0d0)
ax(i) = ax(i) + force * dx
ay(i) = ay(i) + force * dy
ax(j) = ax(j) - force * dx
ay(j) = ay(j) - force * dy
zpe = zpe + pot
end if
end do
end do
end subroutine
!
!====================================================
!
subroutine cellp(xnew, ynew, vx, vy, Sx, Sy)
implicit real(8) (a-h, o-z)
if(xnew < 0) xnew = xnew +sx
if(xnew > sx) xnew = xnew - sx
if(ynew < 0) ynew = ynew + sy
if(ynew > sy) ynew = ynew - sy
end subroutine
!
!====================================================
!
subroutine output(zke, zpe, sx, sy, dt, n, ntime)
implicit real(8) (a-h, o-z)
data iff/0/
if(iff == 0) then
iff = 1
write(6,*) ' ke pe tot'
end if
zke = 0.5d0 * zke / ntime
zpe = zpe / ntime
tot = zke + zpe
write(6, "(6(1x, e13.6))") zke, zpe, tot
zke = 0.0d0
zpe = 0.0d0
end subroutine
!
! Генератор псевдослучайных чисел
!
subroutine rndm(ran)
implicit real*8(a-h,o-z)
data a31/2147483647.d0/, mul/16807.d0/, x/268435451.d0/
t = dmod(x * mul, a31)
ra = t
x = t
ran = ra / a31
end subroutine
Приложение. Рекомендации по выполнению работы
Задание 1
Исходный текст последовательного варианта программы снабжен комментариями.
Задание 3
Применение третьего закона Ньютона:

позволяет сократить объем вычислений в цикле примерно в 2 раза.
Следующий прием основан на введении «радиуса обрезания»  и разбиении всех частиц на две группы по отношению к данной:
и разбиении всех частиц на две группы по отношению к данной:
- частицы, для которых
 ;
; - частицы, для которых
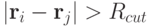 .
.
 выбирается таким образом, чтобы частицы из первой группы давали основной вклад во взаимодействие. Выбор обычно выполняется эмпирически, то есть, на основе пробных расчетов.
выбирается таким образом, чтобы частицы из первой группы давали основной вклад во взаимодействие. Выбор обычно выполняется эмпирически, то есть, на основе пробных расчетов.
При вычислении силы сумма делится на две подсуммы по группам частиц:
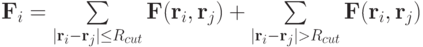
Если вклад от удаленных частиц пересчитывать реже, чем от частиц, для которых  , трудоемкость вычисления силы уменьшится.
, трудоемкость вычисления силы уменьшится.
