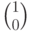Передача информации
Декодирование линейного кода по синдрому
Путь  - матрица размера
- матрица размера 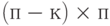 и ранга
и ранга  над полем
над полем 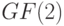 . Эта матрица задает линейное отображение
. Эта матрица задает линейное отображение  пространства
пространства 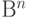 в пространство
в пространство 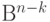 по формуле
по формуле 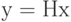 . Ядро этого линейного отображения или множество решений уравнения
. Ядро этого линейного отображения или множество решений уравнения 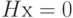 , образующее подпространство пространства
, образующее подпространство пространства 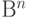 , является линейным кодом. Можно рассмотреть разбиение пространства
, является линейным кодом. Можно рассмотреть разбиение пространства 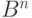 на классы равнообразности. В один класс входят все элементы
на классы равнообразности. В один класс входят все элементы 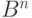 , которые при отображении
, которые при отображении  переходят в один и тот же элемент пространства
переходят в один и тот же элемент пространства 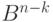 . Элемент пространства
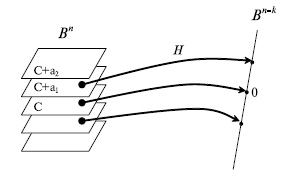
. Элемент пространства 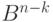 , в который переходят все элементы одного класса, называется синдромом. Pис.7.8 иллюстрирует разбиение пространства
, в который переходят все элементы одного класса, называется синдромом. Pис.7.8 иллюстрирует разбиение пространства 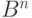 на классы равнообразности.
на классы равнообразности.
Отображение  является отображением на все пространство
является отображением на все пространство 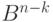 . Для систематической матрицы H это практически очевидно. Действительно, для любого
. Для систематической матрицы H это практически очевидно. Действительно, для любого  можно найти (построить)
можно найти (построить)  , такой, что
, такой, что 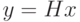 .
.
Произведение 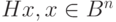 называется синдромом [29], [33]. Фактически, синдромом вектора
называется синдромом [29], [33]. Фактически, синдромом вектора 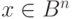 является образ этого вектора при отображении -
является образ этого вектора при отображении -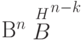 . Все векторы
. Все векторы 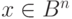 , имеющие один синдром, образуют класс. Так как синдром
, имеющие один синдром, образуют класс. Так как синдром 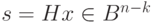 имеет размерность
имеет размерность 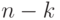 , всего существует
, всего существует 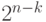 классов (если проверочная матрица имеет ранг
классов (если проверочная матрица имеет ранг 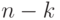 , в частности, если матрица
, в частности, если матрица  имеет систематический вид). Из определения линейного кода следует, что класс, которому соответствует нулевой синдром, является кодом
имеет систематический вид). Из определения линейного кода следует, что класс, которому соответствует нулевой синдром, является кодом  . Каждый класс
. Каждый класс 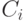 , отличный от кода, порождается "сдвигом"
, отличный от кода, порождается "сдвигом" 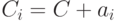 кода
кода  на один из векторов
на один из векторов  класса
класса 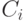 . Действительно, если
. Действительно, если  ., то есть
., то есть 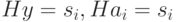 , тогда
, тогда 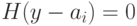 и, следовательно,
и, следовательно,  и
и 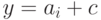 , где
, где 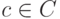 - кодовое слово. Таким образом, любой некодовый вектор, имеющий синдром
- кодовое слово. Таким образом, любой некодовый вектор, имеющий синдром  , можно представить в виде суммы кодового вектора и вектора, имеющего синдром
, можно представить в виде суммы кодового вектора и вектора, имеющего синдром  . Представление такого вида не является единственным. Некодовый вектор
. Представление такого вида не является единственным. Некодовый вектор  в этой сумме можно рассматривать как вектор ошибок, произошедших в тех разрядах кодового слова
в этой сумме можно рассматривать как вектор ошибок, произошедших в тех разрядах кодового слова  , в которых соответствующие компоненты вектора
, в которых соответствующие компоненты вектора  равны 1. Из всех векторов ошибок, имеющих один синдром, наиболее вероятным является вектор
равны 1. Из всех векторов ошибок, имеющих один синдром, наиболее вероятным является вектор 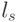 (векторы) с минимальным весом (числом единичных компонент). Такой вектор (векторы) называется лидером класса.
(векторы) с минимальным весом (числом единичных компонент). Такой вектор (векторы) называется лидером класса.
Алгоритм декодирования заключается в следующем. Если получен вектор  и
и 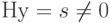 , считаем, что ошибкам соответствует наиболее вероятный вектор из класса
, считаем, что ошибкам соответствует наиболее вероятный вектор из класса 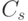 , то есть лидер
, то есть лидер 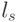 класса
класса 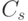 . Тогда декодирование осуществляется в вектор
. Тогда декодирование осуществляется в вектор 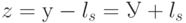 , получающийся из принятого вектора удалением лидера.
, получающийся из принятого вектора удалением лидера.
Рассмотрим пример построения кода по заданной проверочной матрице и декодирования полученного сообщения по синдрому. Пусть дана проверочная матрица 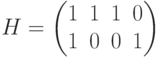 . Запишем уравнение для определения кодовых векторов (слов) для данной матрицы:
. Запишем уравнение для определения кодовых векторов (слов) для данной матрицы:
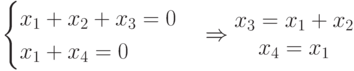
 и
и  которые можно рассматривать как информационные разряды, задаются произвольно (всего 4 варианта 00, 01, 10, 11), а проверочные разряды
которые можно рассматривать как информационные разряды, задаются произвольно (всего 4 варианта 00, 01, 10, 11), а проверочные разряды  и
и 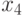 определяются через
определяются через  и
и  . В итоге все кодовые слова определяются из выражения
. В итоге все кодовые слова определяются из выражения
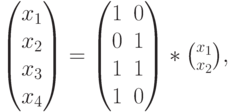
где  и
и 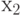 - информационные разряды, а
- информационные разряды, а 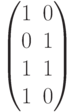 - порождающая матрица, столбцами которой являются кодовые векторы.
- порождающая матрица, столбцами которой являются кодовые векторы.
Кодовые слова, рассматриваемые как векторы-столбцы, образуют матрицу кода
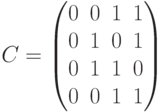
Расстояние кода 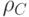 равно минимальному весу ненулевого слова
равно минимальному весу ненулевого слова 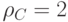 .
.
Найдем смежные классы, которые состоят из векторов пространства 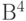 , имеющих одинаковый синдром, и выберем в каждом классе лидера (вектор из класса с минимальным весом).
, имеющих одинаковый синдром, и выберем в каждом классе лидера (вектор из класса с минимальным весом).
Синдромом является любое возможное значение произведения  .
.
В данном случае имеется 4 синдрома: 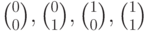 .Каждому синдрому соответствует смежный класс, синдром
.Каждому синдрому соответствует смежный класс, синдром  соответствует коду. Смежные классы (столбцы матриц) для каждого синдрома и выбранные лидеры приведены в таблице.
соответствует коду. Смежные классы (столбцы матриц) для каждого синдрома и выбранные лидеры приведены в таблице.
В третьем смежном классе - два потенциальных лидера с весом (нормой), равным 1. Один из них выбирается в качестве лидера произвольно.
Рассмотрим на этом примере процесс декодирования полученного вектора (слова) с использованием синдромов. Пусть передавался кодовый вектор 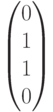 и в процессе переачи произошла ошибка в первом разряде. Это означает, что на приемном конце был получен вектор
и в процессе переачи произошла ошибка в первом разряде. Это означает, что на приемном конце был получен вектор 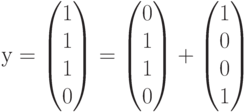 , полученный из переданного вектора
, полученный из переданного вектора 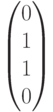 в результате добавления вектора ошибки
в результате добавления вектора ошибки 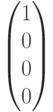 (ошибка в первом разряде). Определим синдром, вычислив произведение
(ошибка в первом разряде). Определим синдром, вычислив произведение  . В данном случае получим
. В данном случае получим 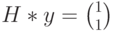 . Это означает, что полученный вектор
. Это означает, что полученный вектор  водит в четвертый смежный класс (см. таблицу). Лидером этого смежного класса является вектор
водит в четвертый смежный класс (см. таблицу). Лидером этого смежного класса является вектор 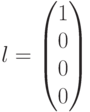 , соответствующий данному синдрому. Вычитая (добавляя) лидер к принятому вектору, производим декодирование
, соответствующий данному синдрому. Вычитая (добавляя) лидер к принятому вектору, производим декодирование 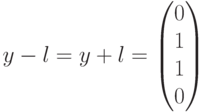 В данном случае декодирование выполнено правильно.
В данном случае декодирование выполнено правильно.