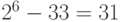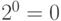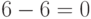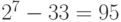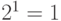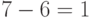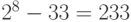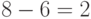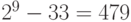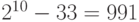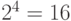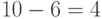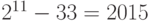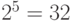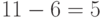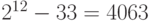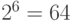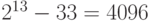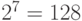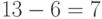Импульсно-кодовое преобразование
Компандирование по µ-закону
Этот закон отличается большим числом дискрет для кодирования сигнала. Их 8159, что позволяет более точно кодировать слабые сигналы. По статистике таковых больше, чем сигналов с большой амплитудой. Это обстоятельство повышает качество речи (но, как показала практика, незначительно). При этом шаги квантования меняются в каждом сегменте и равны 1, 2, 4, 8, 16, 32, 64, 128, 256. Ниже приводится таблица кодирования (табл. 8.4).
При передаче все биты инвертируются.
Алгоритм определения составляющих формата компандирования по рис. 8.6 для числа  иллюстрируется таблицей 8.5 и выполняется в следующем порядке.
иллюстрируется таблицей 8.5 и выполняется в следующем порядке.
-
Знак определяется согласно знаку заданного числа
 и кодируется:
и кодируется:2 — положительная величина отсчета;
3 — отрицательная величина.
-
Номер сегмента
— Находится такое минимальное из возможных чисел
 , что
, что  (точнее,
(точнее, 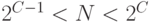 ).
).— Номер сегмента определяется как
 .
. -
Номер шага
Номер шага квантования может быть определен несколькими способами.
1-й способ. После определения номера сегмента вычисляется следующая разность:
 .
.Эта разность переводится в двоичную форму длиной
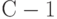 , и в конце двоичной комбинации удаляются
, и в конце двоичной комбинации удаляются 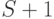 или
или  младших разрядов.
младших разрядов.2-й способ. Определяются разряды номера шага, а именно wyxz.
w определяется следующим образом. Сравниваются числа
 и
и 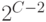 .
.Если
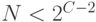 , то
, то  устанавливается новое число
устанавливается новое число  и выполняется шаг
и выполняется шаг  этого алгоритма, в другом случае (
этого алгоритма, в другом случае (  )
) 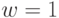 , вычисляется
, вычисляется 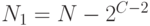 и выполняется пункт b этого алгоритма.
и выполняется пункт b этого алгоритма.Далее сравниваются числа
 и
и 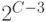 .
.Если
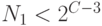 , то
, то  устанавливается новое число
устанавливается новое число 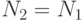 и выполняется следующий шаг этого алгоритма, в другом случае (
и выполняется следующий шаг этого алгоритма, в другом случае ( 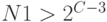 )
) 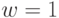 и вычисляется
и вычисляется 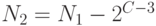 и выполняется следующий шаг этого алгоритма.
и выполняется следующий шаг этого алгоритма.Далее аналогичная процедура выполняется на следующих шагах для
 и
и  .
.
Рассмотрим несколько примеров компандирования отсчетов.
Предположим, нам надо получить все характеристики значения отсчета 68.
Минимальное число, удовлетворяющее условию
 ,
,
это 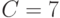 .
.
Тогда десятичный номер сегмента равен 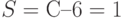 (или двоичное значение 001). Далее вычисляем остаток:
(или двоичное значение 001). Далее вычисляем остаток:
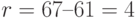
или двоичное значение семи ( 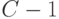 ) оставшихся разрядов равно 000100.
) оставшихся разрядов равно 000100.
Вычислим номер разряда первым способом. Поскольку 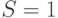 , исключаем 2 последних разряда в двоичном представлении, получаем код шага квантования
, исключаем 2 последних разряда в двоичном представлении, получаем код шага квантования 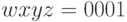 . Полный восьмиразрядный формат равен 0 010 0001.
. Полный восьмиразрядный формат равен 0 010 0001.
Вычислим номер разряда вторым способом.
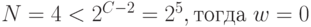 ;
;
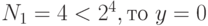 ;
;
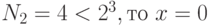 ;
;
 ;
;
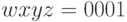 .
.
Полный восьмиразрядный формат равен 0 010 0001.
Рассмотрим число 125.
Из неравенства  получаем
получаем  .
.
Номер сегмента 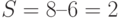 .
.
Остаток 
1-й способ.
Семиразрядное ( 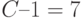 ) Двоичное представление остатка — 0011110. Исключая последние два знака, получаем код шага квантования
) Двоичное представление остатка — 0011110. Исключая последние два знака, получаем код шага квантования 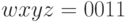 .
.
2-й способ.
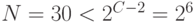 , тогда
, тогда 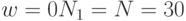 ;
;
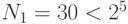 , то
, то  ;
;
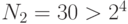 , то
, то 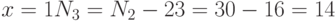 ;
;
 , то
, то 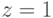 ;
;
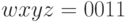 .
.
Полный восьмиразрядный формат равен 0 010 0011.