|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Задачи оптимизации при принятии решений
На рис. 8.4 ради облегчения восприятия четыре прямые обозначены номерами (1) - (4). Прямая (1) описывается уравнением 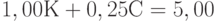 (ограничение по веществу Н). Она проходит, как и показано на рисунке, через точки (5, 0) на оси абсцисс и (0, 20) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (1) или на ней, в отличие от ранее рассмотренных случаев в предыдущей производственной задаче линейного программирования.
(ограничение по веществу Н). Она проходит, как и показано на рисунке, через точки (5, 0) на оси абсцисс и (0, 20) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (1) или на ней, в отличие от ранее рассмотренных случаев в предыдущей производственной задаче линейного программирования.
Прямая (2) - это прямая  (ограничение по калориям). Обратим внимание, что в области неотрицательных С она расположена всюду ниже прямой (1). Действительно, это верно при
(ограничение по калориям). Обратим внимание, что в области неотрицательных С она расположена всюду ниже прямой (1). Действительно, это верно при  , прямая (1) проходит через точку (0, 20), а прямая (2) - через расположенную ниже точку (0, 400/120). Точка пересечения двух прямых находится при решении системы уравнений
, прямая (1) проходит через точку (0, 20), а прямая (2) - через расположенную ниже точку (0, 400/120). Точка пересечения двух прямых находится при решении системы уравнений

Из первого уравнения  . Подставим во второе:
. Подставим во второе: 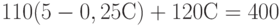 , откуда
, откуда  . Следовательно,
. Следовательно,  , т.е. решение достигается при отрицательном С. Это и означает, что при всех положительных С прямая (2) лежит ниже прямой (1). Значит, если выполнено ограничение по Н, то обязательно выполнено и ограничение по калориям. Мы столкнулись с новым явлением - некоторые ограничения с математической точки зрения могут оказаться лишними. С экономической точки зрения они необходимы, отражают существенные черты постановки задачи, но в данном случае внутренняя структура задачи оказалась такова, что ограничение по калориям не участвует в формировании допустимой области параметров и нахождении решения.
, т.е. решение достигается при отрицательном С. Это и означает, что при всех положительных С прямая (2) лежит ниже прямой (1). Значит, если выполнено ограничение по Н, то обязательно выполнено и ограничение по калориям. Мы столкнулись с новым явлением - некоторые ограничения с математической точки зрения могут оказаться лишними. С экономической точки зрения они необходимы, отражают существенные черты постановки задачи, но в данном случае внутренняя структура задачи оказалась такова, что ограничение по калориям не участвует в формировании допустимой области параметров и нахождении решения.
Прямая (4) - это прямая  (ограничение по веществу Т). Она проходит, как и показано на рисунке, через точки (10, 0) на оси абсцисс и (0, 4) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (4) или на ней, как и для прямой (1).
(ограничение по веществу Т). Она проходит, как и показано на рисунке, через точки (10, 0) на оси абсцисс и (0, 4) на оси ординат. Обратите внимание, что допустимые значения параметров (К, С) лежат выше прямой (4) или на ней, как и для прямой (1).
Следовательно, область допустимых значений параметров (К, С) является неограниченной сверху. Из всей плоскости она выделяется осями координат (лежит в первом квадранте) и прямыми (1) и (4) (лежит выше этих прямых, а также включает граничные отрезки). Область допустимых значений параметров, т.е. точек (К, С), можно назвать "неограниченным многоугольником". Минимум целевой функции  может достигаться только в вершинах этого "многоугольника". Вершин всего три. Это пересечения с осями абсцисс (10, 0) и ординат (0, 20) прямых (1) и (4) (в каждом случае из двух пересечений берется то, которое удовлетворяет обоим ограничениям). Третья вершина - это точка А пересечения прямых (1) и (4), координаты которой находятся при решении системы уравнений
может достигаться только в вершинах этого "многоугольника". Вершин всего три. Это пересечения с осями абсцисс (10, 0) и ординат (0, 20) прямых (1) и (4) (в каждом случае из двух пересечений берется то, которое удовлетворяет обоим ограничениям). Третья вершина - это точка А пересечения прямых (1) и (4), координаты которой находятся при решении системы уравнений
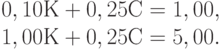
Из второго уравнения  , из первого
, из первого  , откуда
, откуда 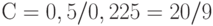 и
и  . Итак,
. Итак, 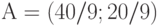 .
.
Прямая (3) на рис. 8.5 - это прямая, соответствующая целевой функции  Она проходит между прямыми (1) и (4), задающими ограничения, и минимум достигается в точке А, через которую и проходит прямая (3). Следовательно, минимум равен
Она проходит между прямыми (1) и (4), задающими ограничения, и минимум достигается в точке А, через которую и проходит прямая (3). Следовательно, минимум равен 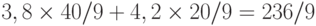 . Задача об оптимизации смеси полностью решена.
. Задача об оптимизации смеси полностью решена.
Двойственная задача, построенная по ранее описанным правилам, имеет приведенный ниже вид (мы повторяем здесь и исходную задачу об оптимизации смеси, чтобы наглядно продемонстрировать технологию построения двойственной задачи):
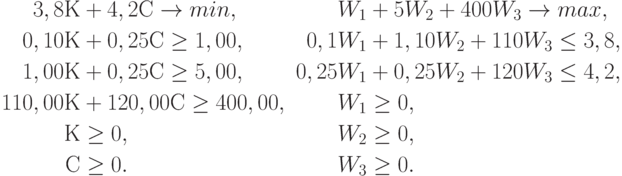
Минимальное значение в прямой задаче, как и должно быть, равно максимальному значению в двойственной задаче, т.е. оба числа равны  . Интерпретация двойственных переменных:
. Интерпретация двойственных переменных: 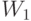 - "стоимость" единицы вещества Т, а
- "стоимость" единицы вещества Т, а 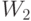 - "стоимость" единицы вещества Н, измеренные "по их вкладу" в целевую функцию. При этом
- "стоимость" единицы вещества Н, измеренные "по их вкладу" в целевую функцию. При этом 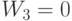 , поскольку ограничение на число калорий никак не участвует в формировании оптимального решения. Итак,
, поскольку ограничение на число калорий никак не участвует в формировании оптимального решения. Итак, 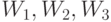 - это т.н. объективно обусловленные оценки (по Л.В. Канторовичу) ресурсов (веществ Т и Н, калорий).
- это т.н. объективно обусловленные оценки (по Л.В. Канторовичу) ресурсов (веществ Т и Н, калорий).
Планирование номенклатуры и объемов выпуска. Вернемся к организации производства. Предприятие может выпускать автоматические кухни (вид кастрюль), кофеварки и самовары. В табл. 8.2 приведены данные о производственных мощностях, имеющихся на предприятии (в штуках изделий).
| Кухни | Кофеварки | Самовары | |
|---|---|---|---|
| Штамповка | 20000 | 30000 | 12000 |
| Отделка | 30000 | 10000 | 10000 |
| Сборка | 20000 | 12000 | 8000 |
| Объем выпуска | Х1 | Х2 | Х3 |
| Удельная прибыль (на одно изделие) | 15 | 12 | 14 |
При этом штамповка и отделка проводятся на одном и том же оборудовании. Оно позволяет штамповать за заданное время или 20000 кухонь, либо 30000 кофеварок, либо и то, и другое, не в меньшем количестве. А вот сборка проводится на отдельных участках.
Задача линейного программирования имеет вид:
 |
( 0) |
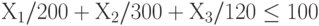 |
( 1) |
 |
( 2) |
 |
( 3) |
 |
( 4) |
 |
( 5) |

Здесь:
(0) - обычное в экономике условие неотрицательности переменных,
(1) - ограничение по возможностям штамповки (выраженное для облегчения восприятия в процентах),
(2) - ограничение по возможностям отделки,
(3) - ограничение по сборке для кухонь,
(4) - то же для кофемолок,
(5) - то же для самоваров (как уже говорилось, все три вида изделий собираются на отдельных линиях).
Наконец, целевая функция  - общая прибыль предприятия.
- общая прибыль предприятия.
Заметим, что неравенство (3) вытекает из неравенства (1), а неравенство (4) - из (2). Поэтому неравенства (3) и (4) можно из формулировки задачи линейного программирования исключить.
Отметим сразу любопытный факт. Как будет установлено, в оптимальном плане 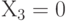 , т.е. самовары выпускать невыгодно.
, т.е. самовары выпускать невыгодно.
Методы решения задач линейного программирования. Методы решения задач линейного программирования относятся к вычислительной математике, а не к экономике. Однако экономисту полезно знать о свойствах интеллектуального инструмента, которым он пользуется.
С ростом мощности компьютеров необходимость применения изощренных математических методов снижается, поскольку во многих случаях время счета перестает быть лимитирующим фактором, оно весьма мало (доли секунд). Поэтому разберем лишь три метода.
Простой перебор. Возьмем некоторый многомерный параллелепипед, в котором лежит многогранник, задаваемый ограничениями. Как его построить? Например, если имеется ограничение типа  , то, очевидно,
, то, очевидно, 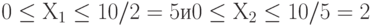 . Аналогичным образом от линейных ограничений общего вида можно перейти к ограничениям на отдельные переменные. Остается взять максимальные границы по каждой переменной. Если многогранник, задаваемый ограничениями, неограничен, как было в задаче о диете, можно похожим, но несколько более сложным образом выделить его "обращенную" к началу координат часть, содержащую решение, и заключить ее в многомерный параллелепипед.
. Аналогичным образом от линейных ограничений общего вида можно перейти к ограничениям на отдельные переменные. Остается взять максимальные границы по каждой переменной. Если многогранник, задаваемый ограничениями, неограничен, как было в задаче о диете, можно похожим, но несколько более сложным образом выделить его "обращенную" к началу координат часть, содержащую решение, и заключить ее в многомерный параллелепипед.
Проведем перебор точек параллелепипеда с шагом  последовательно при
последовательно при  , вычисляя значения целевой функции и проверяя выполнение ограничений. Из всех точек, удовлетворяющих ограничениям, возьмем ту, в которой целевая функция максимальна. Решение найдено! (Более строго выражаясь, найдено с точностью до
, вычисляя значения целевой функции и проверяя выполнение ограничений. Из всех точек, удовлетворяющих ограничениям, возьмем ту, в которой целевая функция максимальна. Решение найдено! (Более строго выражаясь, найдено с точностью до  .)
.)
Направленный перебор. Начнем с точки, удовлетворяющей ограничениям (ее можно найти простым перебором). Будем последовательно (или случайно - с помощью т.н. метода случайного поиска) менять ее координаты на определенную величину  , переходя каждый раз в точку с более высоким значением целевой функции. Если выйдем на плоскость ограничения, будем двигаться по ней (находя одну из координат по уравнению ограничения). Затем движение по ребру (когда два ограничения-неравенства переходят в равенства)… Остановка - в вершине линейного многогранника. Решение найдено! (Более строго выражаясь, найдено с точностью до
, переходя каждый раз в точку с более высоким значением целевой функции. Если выйдем на плоскость ограничения, будем двигаться по ней (находя одну из координат по уравнению ограничения). Затем движение по ребру (когда два ограничения-неравенства переходят в равенства)… Остановка - в вершине линейного многогранника. Решение найдено! (Более строго выражаясь, найдено с точностью до  . Если необходимо, в окрестности найденного решения проводим направленный перебор с шагом
. Если необходимо, в окрестности найденного решения проводим направленный перебор с шагом 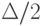 ,
,  и т.д.)
и т.д.)
Симплекс-метод. Этот один из первых специализированных методов оптимизации, нацеленный на решение задач линейного программирования, в то время как методы простого и направленного перебора могут быть применены для решения практически любой задачи оптимизации. Симплекс-метод был предложен американцем Г. Данцигом в 1951 г. Основная его идея состоит в продвижении по выпуклому многограннику ограничений от вершины к вершине, при котором на каждом шаге значение целевой функции улучшается до тех пор, пока не будет достигнут оптимум. Разберем пример на основе данных табл. 8.2.
Рассмотрим задачу линейного программирования, сформулированную выше при рассмотрении оптимизации номенклатуры и объемов выпуска:

Неотрицательность переменных не будем специально указывать, поскольку в задачах линейного программирования это предположение всегда принимается.
В соответствии с симплекс-методом введем т.н. "свободные переменные"  , соответствующие недоиспользованным мощностям, т.е. от системы неравенств перейдем к системе уравнений:
, соответствующие недоиспользованным мощностям, т.е. от системы неравенств перейдем к системе уравнений:
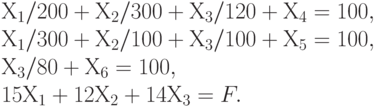
У этой системы имеется очевидное решение, соответствующее одной из вершин многогранника допустимых значений переменных:
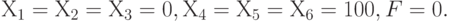
В терминах исходной задачи это означает, что ничего не надо выпускать. Такое решение приемлемо только на период летних отпусков.
В соответствии с симплекс-методом выбираем переменную, которая входит в целевую функцию F с самым большим положительным коэффициентом. Это 
Сравниваем частные от деления свободных членов в первых трех уравнениях на коэффициенты при только что выбранной переменной  :
:

Выбираем строку из системы уравнений, которой соответствует минимальное из всех положительных отношений. В рассматриваемом примере - это первая строка, которой соответствует отношение 20000.
Умножим первую строку на 200, чтобы получить  с единичным коэффициентом:
с единичным коэффициентом:

Затем умножим вновь полученную строку на (-1/300) и сложим со второй строкой, чтобы исключить член с  , получим
, получим

Ту же преобразованную первую строку умножим на (-15) и сложим со строкой, в правой части которой стоит  , получим:
, получим:

В результате система уравнений преобразуется к виду, в котором переменная  входит только в первое уравнение:
входит только в первое уравнение:

Очевидно, у новой системы имеется улучшенное по сравнению с исходным решение, соответствующее другой вершине выпуклого многогранника в шестимерном пространстве:
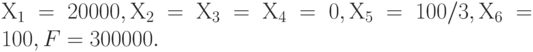
В терминах исходной задачи это решение означает, что надо выпускать только кухни. Такое решение приемлемо, если допустимо выпускать только один вид продукции.

