Рекуррентные сети: Ассоциативная память

Метод Кинцеля. Уничтожение фрустрированных связей.

"Ложная память" имеет интересный нетривиальный смысл и в случае использования других правил обучения, минимизирующих энергию нейронных сетей.

Одно из них было предложено в 1985 году Кинцелем, который основывал свои рассуждения на реальном наблюдении, согласно которому у ребенка в первые несколько лет жизни отмирает большое число синапсов, хотя именно в это время он учится и усваивает огромное количество информации (Kinzel, 1985). Подобное явление подсказало Кинцелю следующий метод обучения. Возьмем полностью неорганизованную сеть нейронов с нулевыми порогами и связями, величины которых имеют Гауссово распределение с нулевым средним, и ликвидируем в ней все фрустрированные в векторах памяти соединения. То есть для всех запоминаемых векторов 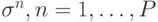обнуляются все связи, для которых 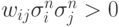. В результате получается сеть, в которой все состояния кодируемые векторами 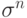, очевидно, будут стационарными.

Требование нефрустрированности каждой связи для всех запоминаемых векторов, конечно, очень сильное. Для слабо коррелированных образов приходится уничтожать так много межнейронных соединений, что в полученной слабосвязанной сети почти все состояния оказываются стабильными, т.е. появляется большое число "ложных" образов. (Если нейроны вообще не связаны - 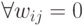, то все возможные состояния сети стационарны). Положение улучшается, если запоминаемые векторы коррелированы друг с другом. Количество стационарных состояний при этом уменьшается, что было продемонстрировано Кинцелем в ходе компьютерного моделирования. Тем не менее, полное число стационарных состояний не может быть уменьшено до набора запоминаемых векторов. Минимальная память в этой сети представляет собой все возможные комбинации векторов минимального базиса, за исключением тех из них, в которых коррелируют состояния нейронов, антикоррелирующие в запоминаемых векторах. Сеть с такой минимальной памятью может быть получена с помощью простой модификации метода уничтожения фрустрированных связей, который стартует с сети, у которой величины всех синаптических связей положительны и равны между собой, и не уничтожает, а инвертирует знак связи, фрустрированной во всех запоминаемых состояний. В примере, иллюстрируемом приводимым ниже рисунком,

в сети из 168 нейронов, организованных в двумерную структуру, запоминаются три образа: (ТФ__) (ТФА_) и (__АК). "Ложными" образами для сети с минимальной памятью будут при этом: пустое поле (____); (__А_); (___К) и их негативы. Невозможно раздельное появление в образе памяти (Т___) и (_Ф__), так как им соответствует один вектор минимального базиса. Невозможно также появление стационарного состояния (ТФ_К), так как в заучиваемых образах присутствие (ТФ__) исключает присутствие (___К) и наоборот.

Неустранимость ложной памяти. Запрещенные наборы

Мы рассмотрели Хеббовское и Кинцелевское правила построения синаптических связей и убедились, что соответствующие сети демонстрируют нетривиальное отображение множества заучиваемых образов на множество аттракторов сети. В частности, ряд аттракторов далеки от заучиваемых образов и квалифицируются как ложная память. Возникает естественный вопрос о существовании такого метода обучения, который вообще бы устранял дополнительную память.

Оказывается, что ответ на него в общем случае отрицательный. Имеются такие наборы образов, что какую бы матрицу синаптических связей и пороги нейронов, гарантирующие их стационарность, мы не выбрали, в сети с неизбежностью возникнут иные аттракторы.

В частности, уже в сети из трех нейронов невозможно обеспечить стационарность только следующих четырех состояний: (0,0,0), (1,1,0), (1,0,1) и (0,1,1) или симметричного набора состояний. Такие наборы векторов, которые не могут составлять и исчерпывать память сети, называют запрещенными. Можно показать, что для сети из трех нейронов два приведенных выше множества векторов исчерпывают все запрещенные наборы образов.

В сети из четырех нейронов не реализуемы уже 40 наборов векторов, но все они могут быть получены всего из двух независимых наборов преобразованием однотипности - перестановками переменных и инверсией^{3Всего существует 402 типа булевых функций четырех переменных, к которым сводится все множество из 65536 функций.} Такая тенденция является обнадеживающей с точки зрения возможностей сетей к запоминанию образов, поскольку доля не реализуемых функций падает. Однако сети, аттракторы которых сконструированы заранее, могут имитировать только ассоциативную память, не создающую новой информации. Нас же сейчас интересует как раз эффект обобщения, присущий рекуррентным сетям, так же как и обычным персептронам.