Обучение с учителем: Распознавание образов

Оптимизация размеров сети

В описанных до сих пор методах обучения значения весов подбиралось в сети с заданной топологией связей. А как выбирать саму структуру сети: число слоев и количество нейронов в этих слоях? Решающим, как мы увидим, является выбор соотношения между числом весов и числом примеров. Зададимся поэтому теперь следующим вопросом:

• Как связаны между собой число примеров P и число весов в сети W?

Ошибка аппроксимации

Рассмотрим для определенности двухслойную сеть (т.е. сеть с одним скрытым слоем). Точность аппроксимации функций такой сетью, как уже говорилось, возрастает с числом нейронов скрытого слоя. При нейронах ошибка оценивается как 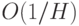. Поскольку число выходов сети, как правило, много меньше числа входов, основное число весов в двухслойной сети сосредоточено в первом слое, т.е. 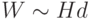. В этом случае средняя ошибка аппроксимации выразится через общее число весов в сети следующим образом:

где d - размерность входов.

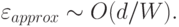
Наши недостатки, как известно - продолжения наших достоинств. И упомянутая выше универсальность персептронов превращается одновременно в одну из главных проблем обучающихся алгоритмов, известную как проблема переобучения.

Переобучение

Суть этой проблемы лучше всего объяснить на конкретном примере. Пусть обучающие примеры порождаются некоторой функцией, которую нам и хотелось бы воспроизвести. В теории обучения такую функцию называют учителем. При конечном числе обучающих примеров всегда возможно построить нейросеть с нулевой ошибкой обучения, т.е. ошибкой, определенной на множестве обучающих примеров. Для этого нужно взять сеть с числом весов большим, чем число примеров. Действительно, чтобы воспроизвести каждый пример у нас имеется P уравнений для W неизвестных. И если число неизвестных меньше числа уравнений, такая система является недоопределенной и допускает бесконечно много решений. В этом-то и состоит основная проблема: у нас не хватает информации, чтобы выбрать единственное правильное решение - функцию-учителя. В итоге выбранная случайным образом функция дает плохие предсказания на новых примерах, отсутствовавших в обучающей выборке, хотя последнюю сеть воспроизвела без ошибок. Вместо того, чтобы обобщить известные примеры, сеть запомнила их. Этот эффект и называется переобучением.

На самом деле, задачей теории обучения является не минимизация ошибки обучения, а минимизация ошибки обобщения, определенной для всех возможных в будущем примеров. Именно такая сеть будет обладать максимальной предсказательной способностью. И трудность здесь состоит в том, что реально наблюдаемой является именно и только ошибка обучения. Ошибку обобщения можно лишь оценить, опираясь на те или иные соображения.

В этой связи вспомним изложенный в начале этой лекции принцип минимальной длины описания. Согласно этому общему принципу, ошибка предсказаний сети на новых данных определяется общей длиной описания данных с помощью модели вместе с описанием самой модели:

Первый член этого выражения отвечает наблюдаемой ошибке обучения. Мы оценили его выше. Теперь обратимся к оценке второго члена, регуляризирующего обучение.

Ошибка, связанная со сложностью модели

Описание сети сводится, в основном, к передаче значений ее весов. При заданной точности такое описание потребует порядка

бит. Следовательно удельную ошибку на один пример, связанную со сложностью модели, можно оценить следующим образом:

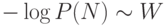
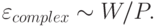
Она, как мы видим, монотонно спадает с ростом числа примеров.

Действительно, для однозначного определения подгоночных параметров (весов сети) по заданным примерам необходимо, чтобы система уравнений была переопределена, т.е. число параметров было больше числа уравнений. Чем больше степень переопределенности, тем меньше результат обучения зависит от конкретного выбора подмножества обучающих примеров. Определенная выше составляющая ошибки обобщения, как раз и связана с вариациями решения, обусловленными конечностью числа примеров^{2Поэтому эту часть ошибки называют в литературе variance, тогда как часть, связанную с точностью аппроксимации - bias. Оптимизация же этих двух составляющих известна как bias-variance dilemma.}

Оптимизация размера сети

Итак, мы оценили обе составляющих ошибки обобщения сети. Важно, что эти составляющие по-разному зависят от размера сети (числа весов), что предполагает возможность выбора оптимального размера, минимизирующего общую ошибку:

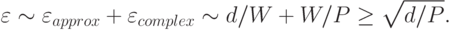
Минимум ошибки (знак равенства) достигается при оптимальном числе весов в сети

соответствующих числу нейронов в скрытом слое равному по порядку величины:

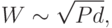
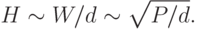
Этот результат можно теперь использовать для получения окончательной оценки сложности обучения (C - от английского complexity)

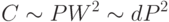
Отсюда можно сделать следующий практический вывод: нейроэмуляторам с производительностью современных персональных компьютеров ( операций в секунду) вполне доступны анализ баз данных с числом примеров 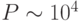и размерностью входов 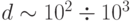. Типичное время обучения при этом составит 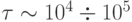секунд, т.е. от десятков минут до несколько часов. Поскольку производственный цикл нейроанализа предполагает обучение нескольких, иногда - многих сетей, такой размер баз данных, представляется предельным для нейротехнологии на персональных компьютерах. Эти оценки поясняют также относительно позднее появление нейрокомпьютинга: для решения практически интересных задач требуется производительность суперкомпьютеров 70-х годов.

Согласно полученным выше оценкам ошибка классификации на таком классе задач порядка 10%. Это, конечно, не означает, что с такой точностью можно предсказывать что угодно. Многие относительно простые задачи классификации решаются с большей точностью, поскольку их эффективная размерность гораздо меньше, чем число входных переменных. Напротив, для рыночных котировок достижение соотношения правильных и неправильных предсказаний 65:35 уже можно считать удачей. Действительно, приведенные выше оценки предполагали отсутствие случайного шума в примерах. Шумовая составляющая ошибки предсказаний должна быть добавлена к полученной выше оценке. Для сильно зашумленных рыночных временных рядов именно она определяет предельную точность предсказаний. Подробнее эти вопросы будут освещены в отдельной лекции, посвященной предсказанию зашумленных временных рядов.

Другой вывод из вышеприведенных качественных оценок - обязательность этапа предобработки высокоразмерных данных. Невозможно классифицировать непосредственно картинки с размерностью 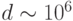. Из оценки точности классификации следует, что это потребует числа обучающих примеров по крайней мере такого же порядка, т.е. сложность обучения будет порядка 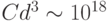. Современным нейрокомпьютерам с производительностью 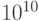операций в секунду потребовалось бы несколько лет обучения распознаванию таких образов. Зрительная система человека, составляющая несколько процентов коры головного мозга, т.е. 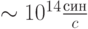обладающая производительностью способна обучаться распознаванию таких образов за несколько часов^{3Ранее, когда речь шла о мозге как управляющем устройстве, мы оценивали его производительность по числу переключений нейронов. Поскольку здесь речь идет об обучении, т.е. об изменениях в синапсах, производительность оценивается по числу срабатываний синапсов.}. В действительности, зрительный нерв содержит как раз около нервных волокон. Напомним, однако, что в сетчатке глаза содержится порядка клеток-рецепторов. Таким образом, уже в самом глазе происходит существенный этап предобработки исходного сигнала, и в мозг поступает уже такая информация, которую он способен усвоить. (Непосредственное распознавание образов с 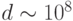потребовало бы обучения на протяжении 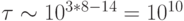секунд, т.е. около 300 лет.)

Методы предобработки сигналов и формирования относительно малоразмерного пространства признаков являются важнейшей составляющей нейроанализа и будут подробно рассмотрены далее в отдельной лекции.