| Россия |
Быстрое дифференцирование, двойственность и обратное распространение ошибки
Теорема 1 (о построении термов). Каждый терм t единственным образом представляется в виде 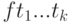 , где f - первый символ в t,
, где f - первый символ в t,  , число k определяется по
, число k определяется по  , а
, а 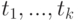 - термы.
- термы.
Эта теорема является точной формулировкой эквивалентности используемой бесскобочной и обычной записи.
Пусть u и v - выражения, то есть последовательности символов алфавита. Скажем, что u входит в v, если существуют такие выражения p и q (возможно, пустые), что v совпадает с puq.
Теорема 2 (о вхождении терма в терм). Пусть 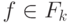 ,
, 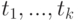 - термы, t представляется в виде
- термы, t представляется в виде 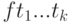 ,
,  - терм и
- терм и  входит в t. Тогда или
входит в t. Тогда или  совпадает с t, или
совпадает с t, или  входит в одно из
входит в одно из 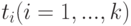 .
.
Доказываются эти теоремы элементарной индукцией по длине термов [3.4]. В доказательстве теоремы 2 выделяется лемма, представляющая и самостоятельный интерес.
Лемма 1. Каждое вхождение любого символа в терм  начинает вхождение некоторого терма в
начинает вхождение некоторого терма в 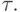
Определим отношение между термами  индуктивным образом "сверху вниз" - по глубине вхождения:
индуктивным образом "сверху вниз" - по глубине вхождения:
-
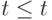 ;
; - если t совпадает с
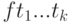 ,
, 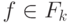 и
и 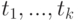 - термы, то
- термы, то 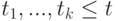 ;
; - если
 и
и  , то
, то  .
.
Согласно теореме 2,  тогда и только тогда, когда
тогда и только тогда, когда 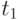 входит в
входит в 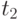 .
.
Для каждого терма t определим множество входящих в него термов 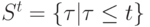 . Если
. Если 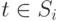 , то при
, то при 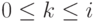 непусты множества
непусты множества  . При этом множество
. При этом множество 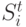 состоит из одного элемента - исходного терма t.
состоит из одного элемента - исходного терма t.
Свяжем с термом t ориентированный граф  с вершинами, взаимнооднозначно соответствующими термам из
с вершинами, взаимнооднозначно соответствующими термам из 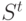 . Будем одинаково обозначать вершины и соответствующие им термы. Пара вершин
. Будем одинаково обозначать вершины и соответствующие им термы. Пара вершин 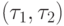 образует ориентированное от
образует ориентированное от 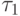 к
к 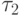 ребро графа
ребро графа  , если терм
, если терм 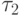 имеет вид
имеет вид 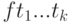 ,
, 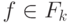 ,
, 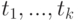 - термы и один из них
- термы и один из них 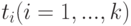 совпадает с
совпадает с 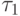 . Вершины графа
. Вершины графа  удобно располагать по слоям
удобно располагать по слоям 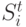 .
.
Для произвольного графа G будем обозначать v(G) множество вершин, а e(G) - множество ребер G.
Возьмем для примера выражение для сложной функции
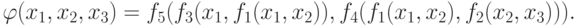 |
( 3) |
В принятой выше бесскобочной префиксной записи оно имеет вид
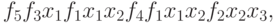 |
( 3') |
где все функциональные символы принадлежат 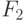 .
.
Граф  для этого терма изображен на рис. 3.1.
для этого терма изображен на рис. 3.1.
Для того, чтобы терм однозначно восстанавливался по графу, необходимы еще два дополнения.
- Сопоставим каждой вершине
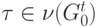 метку
метку 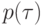 - символ алфавита. Если вершина принадлежит нулевому слою
- символ алфавита. Если вершина принадлежит нулевому слою 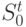 , то ей соответствует терм, совпадающий с символом из
, то ей соответствует терм, совпадающий с символом из 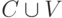 . Этот символ и сопоставляется вершине в качестве метки. Если вершина принадлежит
. Этот символ и сопоставляется вершине в качестве метки. Если вершина принадлежит 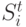 ( i>0 ), то меткой служит функциональный символ: вершине
( i>0 ), то меткой служит функциональный символ: вершине  сопоставляется
сопоставляется  , если
, если  имеет вид
имеет вид 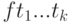 , где
, где 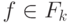 , а
, а 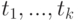 - термы.
- термы. - Каждому ребру
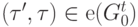 , приходящему в вершину
, приходящему в вершину 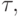 сопоставим метку
сопоставим метку 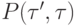 - конечное множество натуральных чисел (номеров): пусть терм
- конечное множество натуральных чисел (номеров): пусть терм  имеет вид
имеет вид 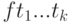 , где
, где 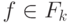 , а
, а 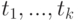 - термы, тогда ребру
- термы, тогда ребру 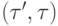 сопоставляется множество тех i (
сопоставляется множество тех i ( 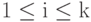 ), для которых
), для которых 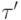 совпадает с
совпадает с 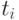 . На практике в большинстве случаев эта метка состоит из одного номера, но возможны и другие варианты - так же, как функции вида f(x,x). Для графических иллюстраций удобно ребра
. На практике в большинстве случаев эта метка состоит из одного номера, но возможны и другие варианты - так же, как функции вида f(x,x). Для графических иллюстраций удобно ребра 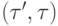 , имеющие в своей метке
, имеющие в своей метке 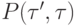 больше одного номера, рисовать как пучок ребер, идущих от вершины
больше одного номера, рисовать как пучок ребер, идущих от вершины 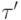 к вершине
к вершине  - по одному такому ребру для каждого номера из
- по одному такому ребру для каждого номера из 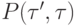 ;
этот номер и будет меткой соответствующего ребра из пучка.
;
этот номер и будет меткой соответствующего ребра из пучка.
Граф  вместе со всеми метками будем обозначать
вместе со всеми метками будем обозначать 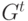 . На рис. 3.1 указаны соответствующие метки для разобранного примера.
. На рис. 3.1 указаны соответствующие метки для разобранного примера.
Итак, для всякого терма t построен ориентированный граф  и две функции: первая сопоставляет каждой вершине
и две функции: первая сопоставляет каждой вершине 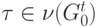 символ алфавита
символ алфавита 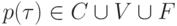 , вторая (обозначим ее P ) - каждому ребру
, вторая (обозначим ее P ) - каждому ребру 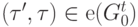 - конечное множество натуральных чисел
- конечное множество натуральных чисел 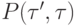 . Отмеченный граф - набор (
. Отмеченный граф - набор ( 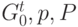 ) обозначаем
) обозначаем 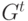 . Функции p и P удовлетворяют следующему ограничению:
. Функции p и P удовлетворяют следующему ограничению:
А) если для данного 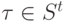 множество входящих ребер
множество входящих ребер 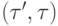 непусто, то
непусто, то 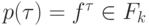 (является k -местным функциональным символом при некотором k ) и семейство множеств
(является k -местным функциональным символом при некотором k ) и семейство множеств
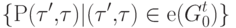
 образует разбиение множества номеров {1,...,k}, то есть
образует разбиение множества номеров {1,...,k}, то есть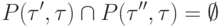
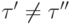 ,
,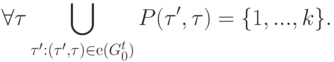
На этом завершается изложение основных формальных конструкций. Прежде, чем переходить к интерпретации, сформулируем теорему об эквивалентности графического и формульного представления термов.
Пусть G - конечный ориентированный граф, не имеющий ориентированных циклов, и в G существует и единственна такая вершина  , к которой от любой вершины ведет ориентированный путь. Пусть, далее, заданы две функции: p - на множестве вершин G со значениями в множестве символов алфавита и P - на множестве ребер G со значениями в множестве конечных наборов натуральных чисел и выполнено условие A.
, к которой от любой вершины ведет ориентированный путь. Пусть, далее, заданы две функции: p - на множестве вершин G со значениями в множестве символов алфавита и P - на множестве ребер G со значениями в множестве конечных наборов натуральных чисел и выполнено условие A.

