| Россия |
Фортран 90
Лабораторная работа 3.1 Оптимизация и распараллеливание вычислительной программы на примере моделирования системы взаимодействующих частиц методом молекулярной динамики
Метод молекулярной динамики
Метод молекулярной динамики является одним из основных методов моделирования динамики систем, состоящих из взаимодействующих между собой частиц. Он применяется в молекулярной физике, астрофизике и других науках. Интерпретация понятия "частица" зависит от предметной области. В молекулярной физике это могут быть атом или молекула, а в астрофизике "частицами" являются звезды или планеты, взаимодействующие с другими астрономическими объектами посредством гравитационного взаимодействия. Динамика систем таких частиц часто описывается уравнениями классической механики.
Будем рассматривать систему N частиц, динамика которых описывается уравнением второго закона Ньютона:
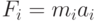
Здесь  - равнодействующая всех сил, действующих на
- равнодействующая всех сил, действующих на  -ю частицу,
-ю частицу,  - ее масса и
- ее масса и  - ускорение, с которым частица двигается под действием силы. Это обыкновенное дифференциальное уравнение второго порядка, которое можно записать в виде:
- ускорение, с которым частица двигается под действием силы. Это обыкновенное дифференциальное уравнение второго порядка, которое можно записать в виде:

Равнодействующая сил, является суммой парных взаимодействий  -й частицы со всеми остальными частицами:
-й частицы со всеми остальными частицами:
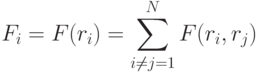
или
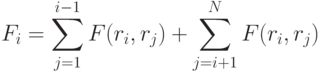
Сила взаимодействия связана с потенциалом взаимодействия. В расчетах молекулярных систем часто используют потенциал Леннарда-Джонса:
![V(r)=4\epsilon \left[ \left(\frac{\sigma}{r}\right)^{12} - \left(\frac{\sigma}{r}\right)^6 \right]](/sites/default/files/tex_cache/d2e96308090ff4c2f8582ab5e467d0c8.png)
Здесь  , а
, а 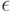 и
и  - параметры потенциала. Первый определяет интенсивность взаимодействия, а второй - положение минимума (см. рис. 6.5).
- параметры потенциала. Первый определяет интенсивность взаимодействия, а второй - положение минимума (см. рис. 6.5).
Потенциал Леннарда-Джонса хорошо описывает взаимодействие между атомами Аргона. Для аргона 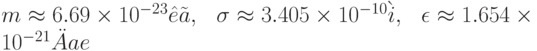 . Будем считать, что массы всех частиц одинаковы,
система единиц выбрана таким образом, что
. Будем считать, что массы всех частиц одинаковы,
система единиц выбрана таким образом, что 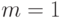 ,
, 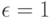 и
и 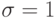 . Тогда сила парного взаимодействия:
. Тогда сила парного взаимодействия:
![F(r_i,r_j)=\frac{24(r_i-r_j)}{{\mid r_i-r_j\mid }^2} \left[\frac{2}{{\mid r_i-r_j\mid }^{12}} - \frac{1}{{\mid r_i-r_j\mid }^6} \right]](/sites/default/files/tex_cache/6cc88848fe3ec8956c836c3eb5eebff6.png)
Интерес могут представлять траектории частиц или термодинамические характеристики системы, например, зависимость температуры от времени:
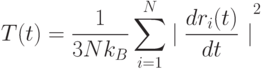
где 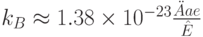 -постоянная Больцмана.
-постоянная Больцмана.
Для вычисления траекторий в методе молекулярной динамики используются различные алгоритмы. Они основаны на замене непрерывного времени дискретным набором значений  ..
Одним из алгоритмов является метод Верле:
..
Одним из алгоритмов является метод Верле:
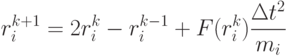
Здесь 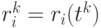 . Наиболее трудоемким является вычисление силы, действующей на частицу.
. Наиболее трудоемким является вычисление силы, действующей на частицу.
Для оптимизации вычисления сил иногда вводится радиус обрезания - некоторый фиксированный (достаточно большой) радиус, такой, что пересчет сил, действующих между частицами, оказавшимися внутри этого радиуса, производится на каждом шаге. Пересчет сил, действующих со стороны более удаленных частиц, производится через несколько шагов. Такая стратегия позволяет уменьшить количество трудоемких операций расчета парных сил. Номера "ближайших" частиц могут храниться в специальном массиве. прТакой массив называется списком.Обычно используются два массива целого типа. Каждый элемент первого массива ( list_nb ) содержит количество ближайших соседей соответствующей частицы:
k0 = 0 j0 = 0 do i = 1, n do j = 1, n if(abs(x(i) - x(j)) < rcutoff) then j0 = j0 + 1 list_nb(i) = j end if end do i_nb(i) = j0 - k0 end do
Во втором массиве содержатся номера соседей каждой частицы. Положения хранятся в элементах, начиная с start(i) и заканчивая finish(i):
start(1) = 1 finish(1) = i_nb(1) do i = 2, n start(i) = finish(i - 1) + 1 finish(i) = finish(i - 1) + i_nb(i) end do
Лабораторная работа
В заданиях лабораторной работы 3.1 предлагается выполнить оптимизацию вычислительной программы. Первый этап оптимизации - сокращение числа операций в последовательном коде на основе использования физических законов. Затем выполняется распараллеливание программы. Выбор инструмента распараллеливания должен быть аргументирован.
Данная работа не предполагает выполнения всех заданий. Учащемуся может быть предложен набор из нескольких заданий, обязательно включающий номера 1, 2 и 3, а также одно или несколько заданий, связанных с распараллеливанием.
По результатам составляется отчет, содержащий решения с обоснованием выбранного метода, результаты измерения быстродействия программы, а также физические результаты и выводы.
Выполнение данной работы рассчитано на несколько занятий (2-6 академических часов). Имеется полный исходный текст программы на языке Fortran 90.
Задания для практической работы
Задание 1
Получить у преподавателя файл с исходным текстом программы и ознакомиться с реализацией метода молекулярной динамики.
Задание 2
Откомпилировать программу, выполнить моделирование для системы с параметрами, заданными преподавателем. Определить процессорное время, потраченное на выполнение моделирования.
Задание 3
Выполнить оптимизацию последовательного кода программы на основе "физических соображений". Определить процессорное время, потраченное на выполнение моделирования. Сравнить с результатом, полученным в задании 2.
Задание 4
Проанализировать последовательный код и выявить участки потенциального параллелизма. Выполнить распараллеливание с помощью OpenMP (если это возможно). Определить процессорное время, потраченное на выполнение моделирования. Сравнить с результатом, полученным в задании 3.
Задание 5
Проанализировать последовательный код, выявить участки потенциального параллелизма и предложить способ распараллеливания в модели передачи сообщений. Выполнить распараллеливание с помощью MPI, используя блокирующие двухточечные операции обмена (если это возможно). Определить процессорное время, потраченное на выполнение моделирования. Сравнить с результатами, полученными в заданиях 3 и 4.
Задание 6
Проанализировать возможность использования других видов обмена (двухточечные неблокирующие, коллективные). Если предполагается выигрыш в производительности, модифицировать вариант программы с использованием MPI. Определить процессорное время, потраченное на выполнение моделирования. Сравнить с результатами, полученными в заданиях 3 , 4 и 5.
Задание 7
Выполнить оптимизацию последовательного кода, полученного при выполнении задания 3, используя введение радиуса обрезания и метод генерации списков частиц. Определить процессорное время, потраченное на выполнение моделирования. Сравнить с результатом, полученным в задании 3.
Задание 8
Провести анализ зависимостей при генерации списков частиц. Выполнить распараллеливание, выбрав наиболее подходящий инструмент. Определить процессорное время, потраченное на выполнение моделирования. Сравнить с результатом, полученным в задании 7.
Задание 9
Выполнить распараллеливание вычисления сил, действующих на частицы, используя метод списков. Определить процессорное время, потраченное на выполнение моделирования. Сравнить с результатом, полученным в заданиях 4 или 5.
Задание 10
Исследовать степень сбалансированности загрузки процессоров (ядер при использовании многоядерной архитектуры). Если сбалансированность неудовлетворительная, предложить способы ее улучшения.
Задание 11
Исследовать масштабируемость программы. Если масштабируемость неудовлетворительная, предложить способы ее улучшения.
Задание 12
На основании результатов, полученных при выполнении заданий данной лабораторной работы, написать отчет, в котором содержатся выводы об эффективности различных способов оптимизации исходного последовательного кода и трудоемкости реализации этих способов на практике.