| Азербайджан |
Контекстно-зависимая классификация
9.4. Алгоритм Витерби (Viterbi)
Пусть задано  столбцов; каждая точка в столбце соответствует
одному из
столбцов; каждая точка в столбце соответствует
одному из  возможных классов
возможных классов 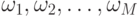 ;
столбцы соответствуют наблюдениям
;
столбцы соответствуют наблюдениям 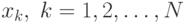 . Стрелками обозначены
переходы от одного класса к другому в последовательности получения наблюдений. Каждая
последовательность классов
. Стрелками обозначены
переходы от одного класса к другому в последовательности получения наблюдений. Каждая
последовательность классов 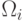 соответствует конкретному маршруту последовательных
переходов. Каждый переход от
соответствует конкретному маршруту последовательных
переходов. Каждый переход от  -го класса к
-го класса к  -му характеризуется
вероятностью
-му характеризуется
вероятностью  , которая предполагается известной. Предположим, что эти
вероятности одинаковы для всех
, которая предполагается известной. Предположим, что эти
вероятности одинаковы для всех  . Далее предположим, что условные
вероятности – плотности
. Далее предположим, что условные
вероятности – плотности 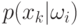 ,
,  ,
, 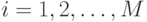 – также известны. Тогда задача максимизации (9.3) ставится как поиск последовательности переходов.
– также известны. Тогда задача максимизации (9.3) ставится как поиск последовательности переходов.
Пусть  – цена, связанная с переходом
– цена, связанная с переходом 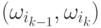 .
Начальное условие при
.
Начальное условие при 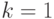 есть
есть 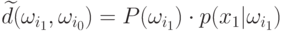 .
Учитывая данные предположения, получаем общую формулу, которую
нужно оптимизировать:
.
Учитывая данные предположения, получаем общую формулу, которую
нужно оптимизировать:


![D_{\max}(\omega_{i_k})=\max_{i_{k-1}=1,2,\ldots,M}
\left[
D_{\max}(\omega_{i_{k-1}})+d(\omega_{i_k},\omega_{i_{k-1}})
\right],
\text{ при }D_{\max}(\omega_{i_0})=0.](/sites/default/files/tex_cache/1837d8f2365e0e97645cfc52efade81d.png)
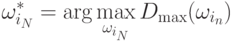
Получаем обратный ход для вычисления 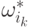 .
Получаем число операций
.
Получаем число операций  , что существенней меньше
, что существенней меньше 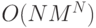 . Данная процедура динамического программирования
известна как алгоритм Витерби.
. Данная процедура динамического программирования
известна как алгоритм Витерби.
9.5. Скрытые Марковские модели
Теперь рассмотрим системы, в которых состояния напрямую не наблюдаются и могут быть лишь оценены из последовательности наблюдений с помощью некоторой оптимизационной техники. Этот тип Марковских моделей известен как скрытые Марковские модели (НММ). НММ – это тип стохастической аппроксимации нестационарных стохастических последовательностей со статистическими свойствами, которые подвергаются различным случайным переходам среди множества различных стационарных процессов. Иными словами, НММ моделирует последовательность наблюдений как кусочно-стационарный процесс.
Такие модели широко используются в распознавании речи. Рассматриваются так называемые высказывания – это может быть слово, часть слова, даже предложение или параграф. Статистические свойства речевого сигнала внутри высказывания подвергаются серии переходов. Например, слово содержит порцию гласных и согласных звуков. Они характеризуются различными статистическими свойствами, которые в свою очередь отражены в переходах в речевых сигналах от одной к другой. Такие примеры дает распознавание рукописного текста, распознавание текстур, где успешно применяется НММ.
НММ есть в основе своей конечный автомат, который генерирует строку
наблюдений – последовательность векторов наблюдений 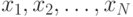 . Таким образом,
НММ содержит
. Таким образом,
НММ содержит  состояний, и строка наблюдений получается как результат
последовательных переходов из одного состояния
состояний, и строка наблюдений получается как результат
последовательных переходов из одного состояния  в другое состояние
в другое состояние  .
Нам подходит так называемая модель "машины Моора", в соответствии с
которой наблюдения получаются как результаты (выходы) из состояний на
прибытие (по переходу) в каждом состоянии.
.
Нам подходит так называемая модель "машины Моора", в соответствии с
которой наблюдения получаются как результаты (выходы) из состояний на
прибытие (по переходу) в каждом состоянии.
Пример. НММ с тремя состояниями. Стрелки обозначают переходы. Такая модель может соответствовать короткому слову с тремя различными стационарными частями, например, для слова "оса".
Модель предоставляет информацию о последовательных переходах между
состояниями  . Такой тип НММ известен как "слева-направо",
поскольку индекс состояний определяется выделенным числом фонем в
одном слове. В действительности, несколько состояний (обычно 3 или 4)
используется для каждой фонемы.
. Такой тип НММ известен как "слева-направо",
поскольку индекс состояний определяется выделенным числом фонем в
одном слове. В действительности, несколько состояний (обычно 3 или 4)
используется для каждой фонемы.