НОУ ИНТУИТ | Математические методы распознавания образов. Лекция 2: Классификация на основе байесовской теории решений

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 30.04.2008 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный университет имени М.В.Ломоносова

|

Вам нравится? Нравится 22 студентам

| Поделиться |

Поддержать программу

2.3. Минимизация среднего риска

Вероятность ошибки классификации – не всегда лучший критерий проверки классификатора. В том случае, когда цена ошибок различного типа существенно различается, лучше использовать другой критерий качества классификации – минимум среднего риска.

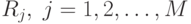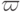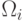Рассмотрим задачу классификации по классам. $R_j, \; j=1,2,\ldots,M$ – области предпочтения классов $\varpi$ . Предположим, что вектор из класса $\Omega_k$ лежит в $R_i, \; i\neq k$ , т.е. классификация происходит с ошибкой. Свяжем с этой ошибкой штраф $\lambda_{ki}$ называемый потерями в результате того, что объект из класса $\Omega_k$ был принят за объект из класса $\Omega_i$ . Обозначим через $L=\|\lambda_{ki}\|$ матрицу потерь.

Определение. Выражение $r_k=\sum_{i=1}^M \lambda_{ki} P\{x\in R_i|\Omega_k\}=\sum_{i=1}^M\lambda_{ki}\int\limits_{R_i}p(x|\Omega_k)dx$ называется риском при классификации объекта класса $\Omega_k$ .

Определение. Выражение $r=\sum_{i=1}^M r_i P(\Omega_i)$ называется общим средним риском.

Теперь мы можем поставить задачу о выборе классификатора, минимизирующего этот риск. Преобразуем выражение общего среднего риска:

$\begin{gathered} r=\sum_{i=1}^M r_k P(\Omega_k)=\sum_{k=1}^M P(\Omega_k)\sum_{i=1}^M\lambda_{ki}\int\limits_{R_i}p(x|\Omega_k)dx= \\ =\sum_{i=1}^M\left( \sum_{k=1}^M P(\Omega_k)\lambda_{ki}\int\limits_{R_i}p(x|\Omega_k)dx\right)= \\ =\sum_{i=1}^M\int\limits_{R_i}\left(\sum_{k=1}^M\lambda_{ki}p(x|\Omega_k)P(\Omega_k)\right)dx \end{gathered}$

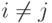Из этого выражения видно, что риск минимален, когда каждый из интегралов в данной сумме минимален, т.е. $x\in R_i$ , если l_i<l_j , при $i\neq j$ , где $l_i=\sum_{k=1}^M\lambda_{ki}p(x|\Omega_k)P(\Omega_k), l_j=\sum_{k=1}^M\lambda_{kj}p(x|\Omega_k)P(\Omega_k)$ .

Пример. Рассмотрим ситуацию радиолокационной разведки. На экране радара отражаются не только цели, но и помехи. Такой помехой может служить стая птиц, которую можно принять за небольшой самолет. В данном случае это двухклассовая задача.

Рассмотрим матрицу штрафов: $L=\|\lambda_{ki}\|,\;i=1,2,\;k=1,2$ . $\lambda_{ki}$ – это штраф за принятие объекта из класса за объект класса . Тогда

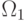$\begin{gathered} l_1=\lambda_{11}p(x|\Omega_1)P(\Omega_1)+\lambda_{21}p(x|\Omega_2)P(\Omega_2)\\ l_2=\lambda_{12}p(x|\Omega_1)P(\Omega_1)+\lambda_{22}p(x|\Omega_2)P(\Omega_2) \end{gathered}$

Пусть

относится у классу $\Omega_1$ , если l_1<l_2

, т.е.

$\begin{gathered} \lambda_{11}p(x|\Omega_1)P(\Omega_1)+\lambda_{21}p(x|\Omega_2)P(\Omega_2)< \lambda_{12}p(x|\Omega_1)P(\Omega_1)+\lambda_{22}p(x|\Omega_2)P(\Omega_2) \\ (\lambda_{21}-\lambda_{22})p(x|\Omega_2)P(\Omega_2)<(\lambda_{12}-\lambda_{11})p(x|\Omega_1)P(\Omega_1) \end{gathered}$

Т.к. $\lambda_{21}>\lambda_{22}$ и $\lambda_{12}>\lambda_{11}$ , то

$\frac{p(x|\Omega_1)}{p(x|\Omega_2)}>\frac{\lambda_{21}-\lambda_{22}}{\lambda_{12}-\lambda_{11}}\cdot\frac{P(\Omega_2)}{P(\Omega_1)}$

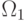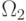Стоящее в левой части неравенства отношение $l_{12}=\frac{p(x|\Omega_1)}{p(x|\Omega_2)}$ называется отношением правдоподобия. Неравенство описывает условие предпочтения класса $\Omega_1$ классу $\Omega_2$ .

Пример. Рассмотрим двухклассовую задачу, в которой для единственного признака известна плотность распределения:

$\begin{gathered} p(x|\Omega_1)=\frac{1}{\sqrt{\pi}}\exp\left(-x^2\right) \\ p(x|\Omega_2)=\frac{1}{\sqrt{\pi}}\exp\left(-(x-1)^2\right) \end{gathered}$

Пусть, также, априорные вероятности $P(\Omega_1)=P(\Omega_2)=\frac12$ .

Задача – вычислить пороги для

a) минимальной вероятности ошибки

b) минимального риска при матрице риска

$L=\begin{pmatrix}0&0.5\\1&0\end{pmatrix}.$

Решение задачи a):

$\begin{gathered} p(x|\Omega_1)P(\Omega_1)=p(x|\Omega_2)P(\Omega_2) \\ \exp\left(-x^2\right)=\exp\left(-(x-1)^2\right) \\ -x^2=-(x-1)^2 \\ \widehat{x}=\frac12 \end{gathered}$

Решение задачи b):

$\begin{gathered} \frac{p(x|\Omega_1)}{p(x|\Omega_2)}=\frac{\lambda_{21}-\lambda_{22}}{\lambda_{12}-\lambda_{11}}\cdot\frac{P(\Omega_2)}{P(\Omega_1)} \\ \frac{\exp\left(-x^2\right)}{\exp\left(-(x-1)^2\right)} \\ -x^2=\ln 2-(x-1)^2 \\ \widetilde{x}=frac12(1-\ln 2) \end{gathered}$

Пример. Рассмотрим двухклассовую задачу с Гауссовскими плотностями распределения $p(x|\Omega_1)\cong N(0,\sigma^2)$ и $p(x|\Omega_2)\cong N(1,\sigma^2)$ и матрицей потерь $L=\begin{pmatrix}0&\lambda_{12}\\ \lambda_{21}&0\end{pmatrix}$ .

Задача – вычислить порог для проверки отношения правдоподобия.

Решение. С учетом матрицы потерь отношение правдоподобия

$\frac{p(x|\Omega_1)}{p(x|\Omega_2)}=\frac{\lambda_{21}-\lambda_{22}}{\lambda_{12}-\lambda_{11}}\cdot\frac{P(\Omega_2)}{P(\Omega_1)}$

запишется в виде

$\frac{p(x|\Omega_1)}{p(x|\Omega_2)}=\frac{\lambda_{21}}{\lambda_{12}}\cdot\frac{P(\Omega_2)}{P(\Omega_1)}$

Запишем плотности распределения

$\begin{gathered} p(x|\Omega_1)=\frac{1}{\sqrt{2\pi\sigma}}\exp\left(-\frac{x^2}{2\sigma^2}\right); \; p(x|\Omega_2)=\frac{1}{\sqrt{2\pi\sigma}}\exp\left(-\frac{(x-1)^2}{2\sigma^2}\right) \\ \frac{p(x|\Omega_1)}{p(x|\Omega_2)}=\frac{\lambda_{21}}{\lambda_{12}}\cdot\frac{P(\Omega_2)}{P(\Omega_1)}= \exp\left(\frac{(x-1)^2}{2\sigma^2}-\frac{x^2}{2\sigma^2}\right) \\ x^2-(x-1)^2=-2\sigma^2 \ln\left(\frac{\lambda_{21}}{\lambda_{12}}\cdot\frac{P(\Omega_2)}{P(\Omega_1)}\right) \\ x=\frac12-\sigma^2\ln\left(\frac{\lambda_{21}}{\lambda_{12}}\cdot\frac{P(\Omega_2)}{P(\Omega_1)}\right) \end{gathered}$

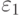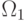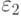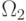Пример. Рассмотрим двухклассовую задачу с матрицей потерь $L=\|\lambda_{ki}\|, \; k=1,2 \, i=1,2$ . Пусть $\varepsilon_1$ – вероятность ошибки, соответствующая вектору из класса $\Omega_1$ и $\varepsilon_2$ – вероятность ошибки, соответствующая вектору из класса $\Omega_2$ . Задача – найти средний риск.

Решение.

$\begin{gathered} r=\sum_{i=1}^M r_k P(\Omega_k)= \\ =\sum_{i=1}^M\left(\sum_{k=1}^M P(\Omega_k)\lambda_{ki}\int\limits_{R_i}p(x|\Omega_k)dx\right)= \\ =\lambda_{11}(1-\varepsilon_1)P(\Omega_1)+ \lambda_{12}\varepsilon_1 P(\Omega_1)+ \lambda_{21}\varepsilon_2 P(\Omega_2)+ \lambda_{22}(1-\varepsilon_2)P(\Omega_2)= \\ =\lambda_{11}P(\Omega_1)+(\lambda_{12}-\lambda_{11})\varepsilon_1 P(\Omega_1)+ (\lambda_{21}-\lambda_{22})\varepsilon_2 P(\Omega_2)+\lambda_{22}P(\Omega_2) \end{gathered}$