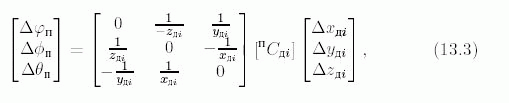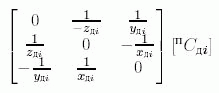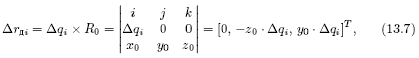НОУ ИНТУИТ | Интеллектуальные робототехнические системы. Лекция 13: Дополнительные встраиваемые элементы контроля в механизмах параллельной структуры

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 18.05.2005 | Уровень: специалист | Доступ: платный | ВУЗ: Московский государственный технологический университет «Станкин»

|

Вам нравится? Нравится 48 студентам

| Поделиться |

Поддержать программу

Погрешности выходного звена

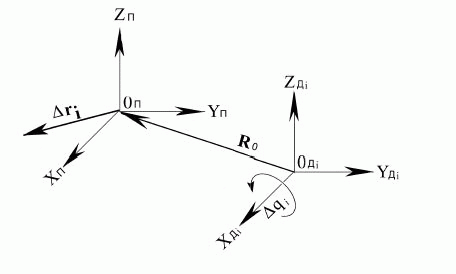
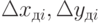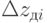Погрешности выходного звена будем рассматривать в системе координат (XYZ)_П. Данные погрешности путем матричных преобразований можно получить в любой другой координатной системе. Определим связь межу погрешностями, представленными в системах (XYZ)_i и (XYZ)_П (рис. 13.2). 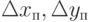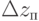С точностью до элементов первого порядка малости погрешности датчиков $\Delta x_{дi},\Delta y_{дi}$ или $\Delta z_{дi}$ приводят к погрешностям вычисления линейных координат $\Delta x_{п},\Delta y_{п}$ и $\Delta z_{п}$

$[\Delta x_{п}\Delta y_{п}\Delta z_{п}]^{T}=^{п}C_{дi}[\Delta x_{дi}\Delta y_{дi}\Delta z_{дi}]^{T} (13.2)$

и погрешностям вычисления угловых координат

Рис. 13.2.

где $[\Delta x_{дi}\Delta y_{дi}\Delta z_{дi}]^{T}$ - вектор, определяющий положение точки 0_дi в системе координат (XYZ)_П (4-й столбец матрицы преобразования координат ^пA_дi ); ^пC_дi - подматрица направляющих косинусов матрицы ^пA_дi.

Как правило, датчики, расположенные в сочленениях звеньев, измеряют только одну из координат x_дi,y_дi или z_дi, поэтому соответствующий данной координате столбец матрицы ^пC_дi в (13.2) или в произведении матриц (13.3)

представляет коэффициенты в матрице K_J (13.1) при одной из координат x_дi,y_дi или z_дi, измеряемой датчиком

$[\Delta x_{п}\Delta y_{п}\Delta z_{п}]^{T}=[K_{1дi}K_{2дi}K_{3дi}]\Delta _{дi} (13.4)$

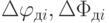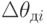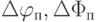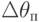Если датчик измеряет один из углов поворота вокруг оси X_дi,Y_дi или Z_дi, то погрешности $\Delta \varphi _{дi},\Delta \Phi _{дi}$ или $\Delta \theta _{дi}$ приводят к погрешности вычисления угловых координат $\Delta \varphi _{п},\Delta \Phi _{п}$ или $\Delta \theta _{п}$ , определяемых соотношением

$[\Delta \varphi _{п}\Delta \Phi _{п}\Delta \theta _{п}]^{T}=^{п}C_{дi}[\Delta \varphi _{дi}\Delta \Phi _{дi}\Delta \theta _{дi}]^{T} (13.5)$

Для каждой одной угловой координаты, измеряемой датчиком, коэффициенты K_J в (13.1) представляют столбец в матрице ^пC_дi при этой координате

$[\Delta \varphi _{п}\Delta \Phi _{п}\Delta \theta _{п}]^{T}=[K_{1дi}K_{2дi}K_{3дi}]\Delta _{дi} (13.6)$

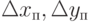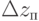Задача определения линейных погрешностей $\Delta x_{п}, \Delta y_{п}$ и $\Delta z_{п}$ в системе координат (XYZ)_П по заданным погрешностям датчиков, измеряющих только угловые координаты в сочленениях звеньев, имеет решение только при измерении одного из углов в системе (XYZ)_дi. На рисунке 13.2 - это угол вращения относительно оси X_дi. Для этого случая связь линейных погрешностей в системе координат (XYZ)_дi с угловой погрешностью датчиков по координате $\Delta q_{i}$ определяется из векторного произведения

где R₀=[x₀y₀z₀]^T - вектор, проведенный из 0_дi в точку 0_п. Координаты R₀ определяются из матрицы ^пA_дi умножением четвертого столбца, взятого с противоположным знаком, на матрицу направляющих косинусов ^пC_дi

[x₀y₀z₀]^T=^пC_дi[-x_дi, -y_дi, -z_дi]^T          (13.8)

В зависимости от выбора направления оси, относительно которой измеряется угол вращения, погрешность $\Delta q_{i}$ в определителе (13.7) записывается во второй строке на первом месте для оси X_дi, на втором месте - для оси Y_дi и на третьем - для оси Z_дi.

Для определения линейной погрешности в системе координат выходного звена (XYZ)_П необходимо 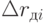$\Delta r_{дi}$ умножить на матрицу направляющих косинусов ^пC_дi

$[\Delta x_{п}\Delta y_{п}\Delta z_{п}]^{T}=^{п}C_{дi}x\Delta r_{дi} (13.9)$

Таким образом, уравнения (13.2)-(13.9) позволяют определять коэффициенты матрицы K_J (13.1), которые устанавливают взаимосвязь между линейными и угловыми погрешностями датчиков и погрешностями перемещения конечного звена механизма в системе координат (XYZ)_П.

Надо отметить, что элементы матрицы ^пA_дi, а следовательно и коэффициенты K_J в (13.1), являются функциями геометрических параметров механизма и измеряемых координат K_J=K_J(q,L), поэтому также вычисляются с погрешностями

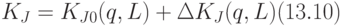
$K_{J}=K_{J0}(q,L)+\Delta K_{J}(q,L) (13.10)$

Подстановкой (13.1) в (13.10) получим

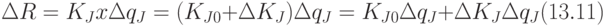
$\Delta R=K_{J}x\Delta q_{J}=(K_{J0}+\Delta K_{J})\Delta q_{J}=K_{J0}\Delta q_{J}+\Delta K_{J}\Delta q_{J} (13.11)$

Однако погрешность

$\Delta K_{J}\Delta q_{J}=(\partial K/\partial q)\Delta q_{J}\Delta q_{i}$

является погрешностью второго порядка малости, поэтому для первого приближения данные погрешности можно принять равными нулю.

Дальше >>

Дмитрий Черепанов

Неоднократно находил ошибки в тестах, особенно в экзаменационных вопросах, когда правильно данный ответ на вопрос определялся в итоге как не правильно отвеченный... Из-за этого сильно страдает конечный бал! Да еще в заблуждение студентов вводит! Они-то думают, что это они виноваты!!! Но они тут не причем! Я много раз проверял ответы на некоторые такие "ошибочные" вопросы по нескольким источникам - результат везде одинаковый! Но ИНТУИТ выдавал ошибку... Как это понимать?

Из-за подобных недоразумений приходиться часами перерешивать экзамен на отличную оценку...!!!

Исправьте, пожалуйста, такие "ошибки"...

ответить