Новый математический аппарат
Теорема об информационном покрытии. Для любой линейной программы граф алгоритма покрывается конечной системой функций, линейных как по пространству итераций, так и по пространству внешних переменных программы. Число этих функций не зависит от значений внешних переменных. Каждая из функций определена на линейном многограннике, расположенном в одном из опорных многогранников со значениями в том же или другом опорном многограннике. Грани многогранников описываются уравнениями, также линейными как по пространству итераций, так и по пространству внешних переменных.
Утверждение теоремы кажется удивительным во многих отношениях. В самом деле, если программа зависит от внешних переменных, то от их значений будет зависеть и граф алгоритма. Из определения графа алгоритма не видно, как влияют на его структуру внешние переменные. Однако, как уже отмечалось, при увеличении значений внешних переменных граф может увеличиваться неограниченно. По условию принадлежности программы линейному классу все свободные члены гиперплоскостей, описывающих грани опорных многогранников, являются функциями, линейно зависящими от внешних переменных. Согласно утверждению теоремы вся зависимость покрывающих функций от внешних переменных сосредоточена в их свободных членах и в свободных членах гиперплоскостей, описывающих грани областей определения. И снова все свободные члены являются функциями, линейно зависящими от внешних переменных. В дополнение к этому напомним, что направляющие векторы гиперплоскостей-граней всех участвующих в рассмотрении многогранников от внешних переменных не зависят. Поэтому все многогранники обладают очень характерным свойством: направления всех их ребер не зависят от значений внешних переменных.
Вершины графа алгоритма любой программы из линейного класса расположены в некоторой системе многогранников, зависящих от внешних переменных. Многогранники меняют свои размеры и конфигурации при изменении этих переменных. Но все эти изменения таковы, что меняются только длины ребер многогранников, а направления ребер остаются постоянными. Разве можно обнаружить это свойство, лишь разглядывая текст линейной программы?
Число покрывающих функций зависит от многих факторов. В частности,
оно зависит от арифметической природы коэффициентов линейных выражений
и числа исполняемых операторов программы. На практике число
покрывающих функций оказывается не очень большим. Исследование
реальных линейных программ показало наличие двух особенностей. Во-первых,
общее число линейных покрывающих функций пропорционально числу
операторов присваивания в программе. Коэффициент пропорциональности не
превосходит нескольких единиц. На меньшее число функций рассчитывать
не приходится, если операторы связаны друг с другом. Во-вторых, почти
всегда система покрывающих функций описывает граф алгоритма абсолютно
точно. В этих случаях для любой покрывающей функции 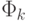 и любой
целочисленной точки
и любой
целочисленной точки  из ее области определения пара точек
из ее области определения пара точек 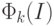 и
и  задает дугу графа алгоритма. Известно лишь несколько реальных
примеров, в которых системы покрывающих функций определяют не граф
алгоритма, а какое-то его расширение.
задает дугу графа алгоритма. Известно лишь несколько реальных
примеров, в которых системы покрывающих функций определяют не граф
алгоритма, а какое-то его расширение.
Итак, вопрос о форме представления дуг в графах алгоритмов, когда сами алгоритмы описаны программами из линейного класса, полностью исследован. Знание одних только покрывающих функций позволяет решать многие интересные задачи: определять параллелизм в циклах, выявлять избыточные вычисления, восстанавливать из программ математические соотношения и т.п. Поэтому, естественно, возникает вопрос о разработке метода определения покрывающих функций по текстам программ. Для программ из линейного класса такой метод построен [ 1 ] . Он достаточно сложен, но эффективен по времени реализации. Тем не менее, мы не будем здесь его обсуждать, поскольку показ устройства самого метода не демонстрирует никакие новые идеи, полезные для понимания процессов изучения информационной структуры алгоритмов.
Несколько ранее было показано, что линейные обобщенные развертки могут служить весьма эффективным инструментом для изучения структуры алгоритмов, в том числе, на макроуровне. Однако необходимым условием для их применения являлось размещение вершин графа алгоритма в линейном арифметическом пространстве со скалярным произведением. В целом пространство итераций не является таковым. Поэтому прежде всего нужно понять, можно ли в этом пространстве построить аналог обобщенных линейных разверток. Рассмотрим в пространстве итераций вещественный функционал, обладающий следующими свойствами:
- его область определения есть линейный замкнутый многогранник, принадлежащий одному из опорных многогранников;
- он линеен как по точкам опорного пространства, так и по внешним переменным.
Будем искать развертки, представленные системой подобных функционалов. Если такие развертки существуют, то будем их называть кусочно-линейными.
Имеется определенное сходство между системой покрывающих функций и рассматриваемыми линейными функционалами. Но между ними существует и принципиальное различие. Пусть граф алгоритма представлен системой покрывающих функций. Многогранники, на которых они определены, могут пересекаться по пространству итераций и никогда не покрывают его полностью. Допустим, что развертку можно представить системой линейных функционалов. В этом случае многогранники, на которых заданы функционалы, не могут пересекаться по пространству итераций и обязаны в совокупности покрывать его полностью.
Рассмотрим случай, когда область определения каждого из линейных
функционалов совпадает с одним из опорных многогранников  .
Пусть покрывающие функции графа алгоритма определены на многогранниках
.
Пусть покрывающие функции графа алгоритма определены на многогранниках  . Как уже говорилось, эти многогранники могут пересекаться и
иметь разные размерности. Если многогранник
. Как уже говорилось, эти многогранники могут пересекаться и
иметь разные размерности. Если многогранник  имеет непустое
пересечение с многогранником
имеет непустое
пересечение с многогранником 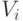 то по построению он входит в
то по построению он входит в 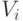 полностью. Рассмотрим векторы
полностью. Рассмотрим векторы 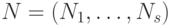 внешних переменных.
Предположим, что они принадлежат некоторой совокупности
многогранников, в общем случае неограниченных. Ясно, что координаты
вершин всех рассматриваемых здесь многогранников
внешних переменных.
Предположим, что они принадлежат некоторой совокупности
многогранников, в общем случае неограниченных. Ясно, что координаты
вершин всех рассматриваемых здесь многогранников  и
и  являются неоднородными линейными функциями переменных
являются неоднородными линейными функциями переменных 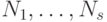 .
Координаты же вершин многогранников, задающих внешние переменные,
постоянны.
.
Координаты же вершин многогранников, задающих внешние переменные,
постоянны.
Допустим, что заданная на многограннике  покрывающая функция
имеет вид
покрывающая функция
имеет вид 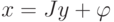 и ее значения принадлежат
и ее значения принадлежат 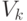 . Здесь
. Здесь 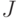 есть числовая
матрица, вектор
есть числовая
матрица, вектор  линейно зависит от внешних переменных. Согласно
теореме об информационном покрытии, граф алгоритма линейной программы
удовлетворяет этим требованиям. Пусть обобщенная развертка имеет вид
линейно зависит от внешних переменных. Согласно
теореме об информационном покрытии, граф алгоритма линейной программы
удовлетворяет этим требованиям. Пусть обобщенная развертка имеет вид 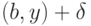 на
на 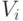 и вид
и вид 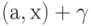 на
на 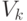 .
Направляющие векторы
.
Направляющие векторы 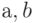 и свободные
члены
и свободные
члены 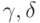 неизвестны и подлежат нахождению. Будем искать векторы
неизвестны и подлежат нахождению. Будем искать векторы 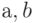 как не зависящие от переменных
как не зависящие от переменных 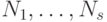 , а свободные члены
, а свободные члены 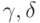 как
неоднородные линейные функции от этих переменных. Так как из
функционалов
как
неоднородные линейные функции от этих переменных. Так как из
функционалов 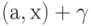 и
и 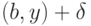 должна составляться обобщенная
развертка, то для всех
должна составляться обобщенная
развертка, то для всех  обязано выполняться неравенство
обязано выполняться неравенство  или, другими словами
или, другими словами 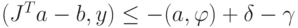 .
.
Обозначим через 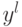 вершины многогранника
вершины многогранника  . Из теории линейных
неравенств известно, что каждая точка ограниченного линейного
многогранника может быть представлена как выпуклая линейная комбинация
его вершин. Следовательно, последнее неравенство эквивалентно такой
системе неравенств
. Из теории линейных
неравенств известно, что каждая точка ограниченного линейного
многогранника может быть представлена как выпуклая линейная комбинация
его вершин. Следовательно, последнее неравенство эквивалентно такой
системе неравенств  . .
Векторы
. .
Векторы 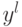 и
и  являются
неоднородными линейными функциями от
являются
неоднородными линейными функциями от 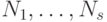 . Эти переменные
принадлежат некоторой системе многогранников, в общем случае
неограниченных. Каждая точка неограниченного линейного многогранника
может быть представлена как выпуклая линейная комбинация его вершин и
направляющих векторов неограниченных ребер. Принимая во внимание это
представление, уже не трудно свести последнюю систему неравенств к
системе неравенств относительно координат векторов
. Эти переменные
принадлежат некоторой системе многогранников, в общем случае
неограниченных. Каждая точка неограниченного линейного многогранника
может быть представлена как выпуклая линейная комбинация его вершин и
направляющих векторов неограниченных ребер. Принимая во внимание это
представление, уже не трудно свести последнюю систему неравенств к
системе неравенств относительно координат векторов  и
коэффициентов разложения свободных членов
и
коэффициентов разложения свободных членов 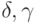 по системе параметров
по системе параметров  [
1
]
.
[
1
]
.
Обозначим через  вектор, составленный для всех многогранников
вектор, составленный для всех многогранников 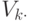 из координат направляющих векторов
из координат направляющих векторов  и коэффициентов разложения
свободных членов
и коэффициентов разложения
свободных членов  по параметрам
по параметрам  . Будем называть его направляющим вектором кусочно-линейной развертки. Зафиксируем какой-нибудь
многогранник, в котором определен вектор внешних переменных
. Будем называть его направляющим вектором кусочно-линейной развертки. Зафиксируем какой-нибудь
многогранник, в котором определен вектор внешних переменных  .
Соберем далее вместе неравенства для всех покрывающих функций графа.
Левую их часть можно представить в виде произведения
.
Соберем далее вместе неравенства для всех покрывающих функций графа.
Левую их часть можно представить в виде произведения 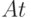 , где
, где  есть
числовая матрица. Проведенные исследования показывают, что имеет
место
есть
числовая матрица. Проведенные исследования показывают, что имеет
место
Теорема о кусочно-линейных развертках. Для любой программы из
линейного класса и любого многогранника, задающего область изменения
внешних переменных, существует не зависящая от значений внешних
переменных матрица  такая, что любой ненулевой вектор
такая, что любой ненулевой вектор  ,
удовлетворяющий векторному неравенству
,
удовлетворяющий векторному неравенству 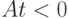 , является направляющим
вектором кусочно-линейной развертки.
, является направляющим
вектором кусочно-линейной развертки.
Эта теорема совместно с теоремой об информационном покрытии создает
мощный математический аппарат для исследования структуры графов
алгоритмов. Находить развертки из системы неравенств можно, например,
с помощью симплекс-метода. Ответ на вопрос, существуют ли кусочно-
линейные развертки, не связанные с решением неравенства 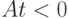 ,
определяется тем, насколько избыточно набор покрывающих функций
описывает граф алгоритма. Как уже отмечалось, графы алгоритмов для
реальных программ почти всегда описываются точно. Если многогранники
,
определяется тем, насколько избыточно набор покрывающих функций
описывает граф алгоритма. Как уже отмечалось, графы алгоритмов для
реальных программ почти всегда описываются точно. Если многогранники 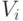 и
и  фиксированы,
то остается зависимость матрицы
фиксированы,
то остается зависимость матрицы  от многогранника, в котором заданы
внешние переменные. В том случае, когда область определения внешних
переменных состоит из нескольких многогранников, направляющие векторы
кусочно-линейных разверток для каждого из многогранников будут
удовлетворять своей системе неравенств.
от многогранника, в котором заданы
внешние переменные. В том случае, когда область определения внешних
переменных состоит из нескольких многогранников, направляющие векторы
кусочно-линейных разверток для каждого из многогранников будут
удовлетворять своей системе неравенств.
Знание графа и его разверток для алгоритма, описанного программой из линейного класса, позволяет решать практически все вопросы, связанные с его информационной и, в том числе, параллельной структурой [ 1 ] . Принадлежность программы к линейному классу устанавливается довольно просто - нужно всего лишь проверить выполнение описанных выше условий. Однако имеется огромное число программ, формально не являющихся линейными, но которые могут быть сведены к таковым после некоторых преобразований.
Набор таких преобразований очень велик и постоянно расширяется. В
частности, в него входят прямая подстановка переменных при вычислении
параметров циклов, преобразование циклов go to в циклы 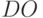 , уточнение
вида многогранников
, уточнение
вида многогранников 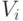 , за счет учета влияния ветвлений, а также более
аккуратное описание многогранников, задающих внешние переменные.
Нередко при написании программ возникают нелинейные индексные
выражения просто потому, что есть настоятельная необходимость экономии
памяти при задании массивов данных. В действительности анализ
структуры таких программ не намного сложнее анализа линейных программ.
Как правило, при анализе структуры программ не требуется детально
учитывать внутреннюю структуру подпрограмм, функций и каких-то
отдельных частей самих программ. Замена соответствующих фрагментов
условными программами специального вида также дает возможность
ограничиться рассмотрением программ из линейного класса. С различными
преобразованиями программ к линейным можно познакомиться в
[
1
]
.
, за счет учета влияния ветвлений, а также более
аккуратное описание многогранников, задающих внешние переменные.
Нередко при написании программ возникают нелинейные индексные
выражения просто потому, что есть настоятельная необходимость экономии
памяти при задании массивов данных. В действительности анализ
структуры таких программ не намного сложнее анализа линейных программ.
Как правило, при анализе структуры программ не требуется детально
учитывать внутреннюю структуру подпрограмм, функций и каких-то
отдельных частей самих программ. Замена соответствующих фрагментов
условными программами специального вида также дает возможность
ограничиться рассмотрением программ из линейного класса. С различными
преобразованиями программ к линейным можно познакомиться в
[
1
]
.
Необходимым этапом выполнения анализа структуры реальных программ является приведение самих программ к некоторому каноническому виду. При этом наибольшие трудности вызывает процесс распутывания их текстов. По существу, общий успех анализа определяется как раз тем, насколько успешно будет проведено это распутывание. Практика показывает поразительные примеры изощренного запутывания текстов программ. Иногда запутывание определяется желанием что-то оптимизировать, но гораздо чаще оно связано с индивидуальным стилем программирования. Стиль программирования редко учитывает то обстоятельство, что при переходе на вычислительные системы другой архитектуры программы придется переписывать. Пока еще правило "программировать надолго - это программировать просто" не стало руководством к действию. Правда, надо признать, что не всегда понятно, что значит "программировать просто". Ясно лишь одно
- простота программирования должна начинаться с простоты, точности и тщательной структурированности математических описаний алгоритмов.
Изложенный выше метод построения графа алгоритма для программ из линейного класса связан с использованием некоторой технологии, основанной на сравнении индексных выражений [ 1 ] . Она непосредственно применима только в тех случаях, когда все индексные выражения в тексте программы заданы явно. Но индексные выражения в программах могут задаваться и неявно с помощью так называемой косвенной адресации. Никаких формальных ограничений на характер индексных выражений при их неявном задании языки программирования не накладывают. Поэтому кажется, что именно косвенная адресация может быть источником появления хаоса в дугах графа алгоритма. Как уже отмечалось, вроде бы близкое к этому расположение дуг даже реализуется на алгоритмах, связанных с нерегулярными и адаптивными сетками. На самом деле разработчики программ, реализующих такие и подобные им алгоритмы, мыслят не терминами хаотических отношений между отдельными операциями, а реализуют какие-то иные, вполне определенные образы отношений. Эти образы и накладывают соответствующие ограничения на реальную косвенную адресацию при разработке конкретных алгоритмов. Для анализа структуры алгоритмов важно уметь выявлять и использовать возникающие ограничения.
Приведем пример того, как можно учитывать подобные ограничения.
Пусть в пространстве  задана область
задана область  . Предположим, что алгоритм
сводится к построению в области
. Предположим, что алгоритм
сводится к построению в области  некоторой упорядоченной
последовательности точек и в вычислении в этих точках значений каких-
то векторных функций. Точки последовательности могут выбираться как
угодно. В частности, часть из них или даже все они могут многократно
повторяться. Функции могут быть сколь угодно сложными, в том числе,
разными в разных точках. Важно только одно - откуда берутся аргументы
при вычислении очередного значения функции.
некоторой упорядоченной
последовательности точек и в вычислении в этих точках значений каких-
то векторных функций. Точки последовательности могут выбираться как
угодно. В частности, часть из них или даже все они могут многократно
повторяться. Функции могут быть сколь угодно сложными, в том числе,
разными в разных точках. Важно только одно - откуда берутся аргументы
при вычислении очередного значения функции.
Допустим, что в пространстве  фиксирован замкнутый острый конус
фиксирован замкнутый острый конус  ,
боковая поверхность которого образована системой гиперплоскостей.
Назовем этот конус опорным и будем перемещать его параллельно самому
себе в пространстве
,
боковая поверхность которого образована системой гиперплоскостей.
Назовем этот конус опорным и будем перемещать его параллельно самому
себе в пространстве  . Единственное ограничение на построение
алгоритма состоит в следующем: если значение функции вычисляется в
точке
. Единственное ограничение на построение
алгоритма состоит в следующем: если значение функции вычисляется в
точке  из области
из области  , то аргументы функции могут браться лишь из тех
построенных точек последовательности, которые попадают в опорный
конус, при условии, что вершина конуса находится в точке
, то аргументы функции могут браться лишь из тех
построенных точек последовательности, которые попадают в опорный
конус, при условии, что вершина конуса находится в точке  . Очень
часто опорный конус берется ограниченным. В этом случае все аргументы
для точки
. Очень
часто опорный конус берется ограниченным. В этом случае все аргументы
для точки  берутся от точек, принадлежащих некоторой ее локальной
окрестности. Построенные таким образом алгоритмы и их графы называются локальными. Отметим, что все локальные алгоритмы легко разбиваются на
параллельно реализуемые фрагменты. Более того, не известны никакие
другие массово используемые структуры, кроме локальных, которые легко
масштабируются под требования многопроцессорных систем с
распределенной памятью.
берутся от точек, принадлежащих некоторой ее локальной
окрестности. Построенные таким образом алгоритмы и их графы называются локальными. Отметим, что все локальные алгоритмы легко разбиваются на
параллельно реализуемые фрагменты. Более того, не известны никакие
другие массово используемые структуры, кроме локальных, которые легко
масштабируются под требования многопроцессорных систем с
распределенной памятью.
Алгоритм, представленный в описанном виде, имеет много достоинств. Не требуется проявлять никакой особой заботы о регулярности расположения дуг. Любой подобный алгоритм прекрасно распараллеливается, так как имеет полный набор обобщенных линейных разверток. В качестве их можно взять, например, линейные функционалы с направляющими векторами, совпадающими с направляющими векторами гиперплоскостей, образующих грани опорного конуса. Эта схема представляет яркий пример алгоритма, имеющего направленный граф.
Как показывает практика, огромное число самых разных алгоритмов
укладывается в описанную схему. Исходя из традиционных описаний
алгоритмов, не всегда в конкретных случаях сразу видны подходящие
образы пространства  , области
, области  опорного конуса
опорного конуса  и
последовательности перебора точек. Но такие образы почти всегда
находятся.
и
последовательности перебора точек. Но такие образы почти всегда
находятся.
С помощью введения какого-то числа дополнительных условных передач
управления любую программу можно свести к тесно вложенному гнезду
циклов. Это может подсказать, как должны выглядеть пространство  и
область
и
область  . Кроме этого, возможность сведения программы к гнезду циклов
подсказывает, что по-видимому во многих случаях граф из пространства
итераций, которое вообще-то устроено достаточно сложно, можно уложить
в какое-то пространство малой размерности. Практика говорит о том, что
такую укладку не только можно осуществить достаточно часто, но и сами
уложенные графы при этом имеют весьма изящную структуру.
Следовательно, такую же изящную структуру имеют и сами алгоритмы.
Задача переноса графа алгоритма из пространства итераций в подходящее
пространство малой размерности называется задачей укладки графа. Она
исключительно интересна и имеет прекрасные прикладные перспективы.
Предположим, что каждый используемый алгоритм будет описан графом, по
которому сразу можно сказать все о структуре самого алгоритма.
Насколько проще станет их изучение и использование!
. Кроме этого, возможность сведения программы к гнезду циклов
подсказывает, что по-видимому во многих случаях граф из пространства
итераций, которое вообще-то устроено достаточно сложно, можно уложить
в какое-то пространство малой размерности. Практика говорит о том, что
такую укладку не только можно осуществить достаточно часто, но и сами
уложенные графы при этом имеют весьма изящную структуру.
Следовательно, такую же изящную структуру имеют и сами алгоритмы.
Задача переноса графа алгоритма из пространства итераций в подходящее
пространство малой размерности называется задачей укладки графа. Она
исключительно интересна и имеет прекрасные прикладные перспективы.
Предположим, что каждый используемый алгоритм будет описан графом, по
которому сразу можно сказать все о структуре самого алгоритма.
Насколько проще станет их изучение и использование!
Иногда для поиска подходящих образов приходится обращаться к каким-то иным интерпретациям алгоритмов. Если исходить из геометрической интерпретации, то в приведенное выше описание сразу укладываются все алгоритмы, использующие явные разностные схемы, в том числе, с нерегулярными и адаптивными сетками. Но если за основу взять матричную их интерпретацию, а в качестве одного из важнейших модулей выбрать умножение разреженной матрицы на вектор, то в такой интерпретации трудно что-то разглядеть.
В связи со сказанным возникает следующая идея. Известно, что одна из трудностей восприятия численных методов, особенно в отношении информационной и параллельной структуры, связана с отсутствием единой методологической основы их изложения. Предложенная схема вполне подходит для такой основы. Она очень проста и для ее понимания не требуются никакие специальные знания об алгоритмах. Начинать обсуждать схему можно на самых ранних этапах компьютерного образования. Наполнять же ее конкретным содержанием вполне возможно по мере необходимости.
Схему легко модифицировать, отказавшись от требований остроты и замкнутости опорного конуса. Подобная модификация позволит распространить ее на алгоритмы с ограниченным ресурсом параллелизма. Единственное, чего не хватает для реализации данной идеи, - это достаточного числа наполнений предложенной схемы конкретными алгоритмами. Но можно надеяться, что создание таких наполнений является лишь вопросом времени.
