Компьютеры и ошибки округления
Требование унифицированного выполнения арифметических операций над числами приводит к необходимости унифицированного изображения в компьютере всех конечных дробей. Будем для простоты рассматривать дроби без знака, считая, что их знак либо учитывается в самой системе счисления, либо изображается каким-то иным способом.
Пусть на изображение каждой дроби отводится одно и то же число  базисных элементов. Ясно, что на
базисных элементов. Ясно, что на  элементах можно изображать не более
элементах можно изображать не более  разрядов любого числа. Чтобы это изображение можно было прочитать,
необходимо установить взаимно однозначное соответствие между базисными
элементами, отведенными для изображения каждого числа, и положением
разрядов в числе относительно запятой. В зависимости от того, является
ли это соответствие одним и тем же для всех изображаемых чисел или
зависит от самого числа, различают два способа представления чисел в
компьютере. Называются они представлением с фиксированной и плавающей
запятой.
разрядов любого числа. Чтобы это изображение можно было прочитать,
необходимо установить взаимно однозначное соответствие между базисными
элементами, отведенными для изображения каждого числа, и положением
разрядов в числе относительно запятой. В зависимости от того, является
ли это соответствие одним и тем же для всех изображаемых чисел или
зависит от самого числа, различают два способа представления чисел в
компьютере. Называются они представлением с фиксированной и плавающей
запятой.
Предположим, что каждые  базисных элементов служат для изображения
базисных элементов служат для изображения  последовательных разрядов чисел. Причем положение этих разрядов
относительно запятой фиксировано и является одним и тем же для всех
дробей. Будем считать, что на изображение разрядов, стоящих слева от
запятой, отводится r элементов, где
последовательных разрядов чисел. Причем положение этих разрядов
относительно запятой фиксировано и является одним и тем же для всех
дробей. Будем считать, что на изображение разрядов, стоящих слева от
запятой, отводится r элементов, где 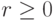 . Такой способ представления
чисел называется представлением с фиксированной запятой. С помощью
этого способа можно точно запоминать любую из конечных p -ичных дробей,
имеющих не более r ненулевых разрядов слева от запятой и не более
. Такой способ представления
чисел называется представлением с фиксированной запятой. С помощью
этого способа можно точно запоминать любую из конечных p -ичных дробей,
имеющих не более r ненулевых разрядов слева от запятой и не более  ненулевых разрядов справа от запятой. Все такие дроби x лежат в
диапазоне -
ненулевых разрядов справа от запятой. Все такие дроби x лежат в
диапазоне - 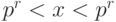 .
.
Один из недостатков представления чисел с фиксированной запятой
виден сразу. Если p -ичная дробь много меньше 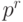 по модулю, то большая часть из отведенных базисных
элементов изображает старшие нулевые разряды и фактически не
используется. Поэтому приближение числа такой дробью связано с большой
относительной ошибкой. Однако для чисел, близких к
по модулю, то большая часть из отведенных базисных
элементов изображает старшие нулевые разряды и фактически не
используется. Поэтому приближение числа такой дробью связано с большой
относительной ошибкой. Однако для чисел, близких к 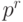 по
модулю, для представления старших ненулевых разрядов используются все
по
модулю, для представления старших ненулевых разрядов используются все  базисных элементов. В этом случае относительная ошибка приближения
числа дробью является минимальной. Абсолютная ошибка представления
чисел с фиксированной запятой всегда лежит в одних и тех же пределах
независимо от величины самих чисел.
базисных элементов. В этом случае относительная ошибка приближения
числа дробью является минимальной. Абсолютная ошибка представления
чисел с фиксированной запятой всегда лежит в одних и тех же пределах
независимо от величины самих чисел.
Представление чисел с плавающей запятой заключается в следующем.
Всякое ненулевое число x можно записать в виде 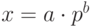 ,
где b - целое число и
,
где b - целое число и 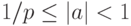 .
Число a называется мантиссой числа x, число b - его порядком. Пусть на изображение порядка без знака отводится r базисных
элементов, на изображение мантиссы без знака
.
Число a называется мантиссой числа x, число b - его порядком. Пусть на изображение порядка без знака отводится r базисных
элементов, на изображение мантиссы без знака  элементов. Если
теперь порядок и мантисса представлены как дроби с фиксированной
запятой, то это и будет представлением числа x с плавающей
запятой.
элементов. Если
теперь порядок и мантисса представлены как дроби с фиксированной
запятой, то это и будет представлением числа x с плавающей
запятой.
Заметим, что порядок всегда представляется точно, так как он
является целым числом. Мантисса же будет представлена точно лишь для
тех p -ичных дробей, которые имеют не более  ненулевых старших
разрядов. Точно или с округлением могут быть представлены с плавающей
запятой только те числа x, порядок которых удовлетворяет неравенству
ненулевых старших
разрядов. Точно или с округлением могут быть представлены с плавающей
запятой только те числа x, порядок которых удовлетворяет неравенству 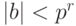 . Независимо от величины этих чисел относительная ошибка их
представления лежит в одних и тех же пределах. Числа, для которых
. Независимо от величины этих чисел относительная ошибка их
представления лежит в одних и тех же пределах. Числа, для которых  ,
не могут быть представлены с плавающей запятой в компьютере с
заданной величиной r. Все числа, для которых
,
не могут быть представлены с плавающей запятой в компьютере с
заданной величиной r. Все числа, для которых  , также как и число
0, заменяются в компьютере числом с нулевой мантиссой. В разных
компьютерах порядок таких чисел может быть разным. Число
, также как и число
0, заменяются в компьютере числом с нулевой мантиссой. В разных
компьютерах порядок таких чисел может быть разным. Число  , для
которого
, для
которого 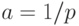 и
и  называется машинным нулем. Оно совпадает с
минимальным положительным числом, которое можно представить с
плавающей запятой в компьютере при заданных числах r и p.
называется машинным нулем. Оно совпадает с
минимальным положительным числом, которое можно представить с
плавающей запятой в компьютере при заданных числах r и p.
В современных компьютерах применяются оба способа представления чисел. Выбор того или иного способа зависит от типа решаемых задач. На компьютерах и больших вычислительных системах широкого назначения нередко допускается использование обеих форм представления чисел.
Операции над числами с фиксированной запятой выполняются быстрее, чем над числами с плавающей запятой. Это связано с тем, что при реализации операций в режиме с плавающей запятой по существу приходится выполнять все действия с парами чисел с фиксированной запятой. Поэтому при решении тех задач, где положение запятой в числовых данных более или менее определено, использование представления чисел с фиксированной запятой позволяет получить ощутимый выигрыш во времени. К таким задачам относятся, например, финансовые расчеты, задачи количественного учета, многие задачи управления и т.п. При решении научно-технических задач более удобно представление чисел с плавающей запятой, поскольку в них, как правило, приходится иметь дело с числовыми данными из очень широкого диапазона.
Умелое использование фиксированной запятой при решении конкретной задачи иногда позволяет добиться большей скорости и большей точности, чем использование плавающей запятой. Еще большего эффекта можно достичь путем разумного сочетания вычислений с фиксированной и плавающей запятой. Однако это тема совсем другой лекции.
Несмотря на то, что каждая из отдельных ошибок округления очень мала, в совокупности они могут оказывать значительное влияние на точность результата, получаемого в процессе реализации алгоритма. Особенно в тех случаях, когда число выполняемых операций достаточно велико. Более того, из-за ошибок округления некоторые алгоритмы просто нельзя реализовать. Поэтому при решении серьезных задач оцениванию влияния ошибок округления уделяется особое внимание.
Имеется много различных подходов к проведению такого оценивания. Гарантированные выводы о точности можно делать только на основе получения мажорантных оценок. Но мажорантные оценки редко достигаются. К тому же их получение требует виртуозного, граничащего с искусством владения соответствующей техникой. В этом можно убедиться на примере оценивания влияния ошибок округления в алгоритмах линейной алгебры [ 2 ] . Поэтому в целях создания более полной картины распределения ошибок округления весьма заманчиво считать отдельные ошибки случайными независимыми величинами. Заманчиво потому, что подобная гипотеза приводит к вероятностным оценкам, существенно лучшим по сравнению с мажорантными. Однако не менее заманчиво считать отдельные ошибки зависимыми случайными величинами, так как можно предположить, что знание характера зависимости также приведет к лучшим оценкам. Но тогда какими же их считать и каковы они в действительности?
В общем случае ответ на этот вопрос связан со сложными теоретико-числовыми исследованиями, знакомство с которыми не входит в нашу задачу. Ограничимся здесь лишь изложением нескольких фактов. Тем не менее, даже эти факты позволят показать интересные свойства ошибок округления и дадут веские основания для выбора правдоподобной гипотезы совместного распределения всей совокупности ошибок округления в вычислительном процессе.
Изучение вероятностных свойств ошибок округления невозможно без внесения в них некоторого элемента случайности. Эту случайность нередко связывают с многократным решением одной и той же задачи на различных компьютерах, с решением задачи при случайном числе верных знаков в промежуточных вычислениях и даже при случайном округлении результатов выполнения арифметических операций. Однако в условиях реальных вычислений внесение случайности можно осуществить, вообще говоря, единственным способом.
На всех современных компьютерах ошибка округления при выполнении любого арифметического действия однозначно определяется значениями его аргументов. Поэтому при фиксированном алгоритме и фиксированных входных данных вся совокупность ошибок округления определяется однозначно и никакой случайности в их поведении возникнуть просто неоткуда. Если алгоритм не связан с какими-нибудь случайными процессами, то единственным источником случайности в ошибках округления может быть лишь случайность входных данных алгоритма.
С точки зрения вычислителей-практиков отношение к входным данным как к случайным величинам вполне оправдано. Они редко бывают известны точно, так как на них влияет много факторов. Чаще всего входные данные алгоритма получаются в результате проведения либо каких-то вычислений, либо каких-то измерений. И то, и другое сопровождается внесением во входные данные дополнительных ошибок, точный учет которых невозможен. Следовательно, при фиксированном алгоритме и способе округления все ошибки округления можно рассматривать как вполне определенные функции случайных входных данных, распределенных совместно по некоторому закону.
Перед обсуждением вероятностных свойств ошибок округления сделаем несколько уточнений. Будем считать, что вычисления проводятся с плавающей запятой, мантиссы всех чисел имеют s разрядов и округление результата выполнения любой операции всегда осуществляется наилучшим образом. Если при выборе наилучшего округления возникает неоднозначность, то будем предполагать, что она разрешается таким образом, чтобы из двух возможностей мантисса округленного числа становилась наибольшей. Это соответствует практике выбора наилучшего округления. Вместо ошибок округления самих чисел будем рассматривать нормированные в масштабе s -го разряда ошибки округления мантисс. При сделанных уточнениях все нормированные ошибки округления будут всегда принадлежать полусегменту (-1/2, +1/2].
До сих пор не создана развитая теория, позволяющая в произвольном вычислительном процессе точно изучать и оценивать ошибки округления как функции случайных входных данных. Однако доказано немало отдельных фактов, которые могут служить веским поводом для выдвижения некоторой правдоподобной вероятностной гипотезы, касающейся их совместного распределения. Общим, как в доказательствах, так и в гипотезе, является рассмотрение распределений нормированных ошибок округления в асимптотике, т.е. в ситуации, когда число разрядов s, отводимых для преставления мантисс чисел, может быть сколь угодно большим.
Любой вычислительный процесс начинается с округления входных данных при их вводе в компьютер. Предположим, что входные данные являются случайными величинами, имеющими непрерывную плотность совместного распределения. Доказано, что независимо от того, какова в действительности эта плотность, все нормированные ошибки округлении при вводе входных данных асимптотически являются случайными попарно независимыми величинами, распределенными равномерно и непрерывно на полусегменте (-1/2, +1/2].
Более интересные результаты дает рассмотрение простейших арифметических операций. Для умножения, деления, сложения и вычитания также доказано, что независимо от того, какова плотность совместного распределения входных данных, нормированные ошибки округления асимптотически являются случайными величинами, распределенными равномерно на полусегменте (-1/2, +1/2]. Но для умножения и деления это распределение снова оказывается непрерывным, а вот для сложения и вычитания оно будет дискретным. При этом во всех сокращенных системах счисления нормированные ошибки округления для сложения и вычитания асимптотически не имеют никакого смещения, а во всех системах с четным основанием ошибки асимптотически всегда имеют ненулевое смещение. Другими словами, математическое ожидание последних ошибок не равно нулю. Не вдаваясь в детали обсуждения, лишь заметим, что появляется этот эффект исключительно за счет того, что в системах счисления с четным основанием обязательно возникает ситуация, когда при правильном округлении существуют два наилучших округленных числа.
Напомним, что все современные компьютеры построены на системах счисления с четным основанием. Следовательно, при использовании на них вероятностной модели ошибок округления нельзя предполагать, что математическое ожидание самих ошибок в общем случае будет равно нулю. Но ведь известно, что ненулевое математическое ожидание ошибок приводит к более быстрому их накоплению! Опять констатируем, что с точки зрения точности системы счисления с четным основанием и, в частности, двоичная система не являются лучшими.
Для некоторых классов алгоритмов, например, реализующих решение задач линейной алгебры, вычисление интегралов и др., поведение ошибок округления исследовано во всей их совокупности. Доказано, что независимо от того, какова плотность совместного распределения входных данных, все нормированные ошибки округления асимптотически являются попарно независимыми случайными величинами. Отдельные ошибки ведут себя так, как описано выше.
Подчеркнем, что все результаты, касающиеся свойств ошибок округления, получены без каких-либо дополнительных предположений об их поведении. Поэтому выполненные исследования и приведенные выше аргументы говорят о том, что при вероятностной оценке суммарного влияния ошибок округления в массовых вычислениях может быть использована следующая
Гипотеза. Все нормированные ошибки округления вычислительного процесса в режиме с плавающей запятой являются случайными попарно независимыми величинами, распределение которых не зависит от входных данных и результатов промежуточных вычислений. Они распределены равномерно на полусегменте (-1/2, +1/2], дискретно для операций сложения и вычитания и непрерывно для большинства других операций. Для операций сложения и вычитания в системах счисления с четным основанием математическое ожидание ошибок не равно нулю. Для непрерывно распределенных ошибок их математическое ожидание равно 0, а дисперсия не превосходит 1/12.
При практическом применении этой гипотезы следует проявлять определенную осторожность в отношении предполагаемых значений математического ожидания и дисперсии ошибок округления, возникающих при выполнении операций сложения и вычитания. Они зависят от разности порядков участвующих в операциях чисел.
Безусловно, в общем случае ошибки округления значительно затрудняют проведение вычислений. Однако иногда умелое использование ошибок округления позволяет успешно решать очень сложные в вычислительном отношении задачи, что подтверждает следующий пример.
Предположим, что ищется вектор  , принадлежащий корневому
подпространству, соответствующему собственному значению
, принадлежащий корневому
подпространству, соответствующему собственному значению  матрицы
матрицы  .
Пусть
.
Пусть 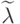 близко к
близко к  . Возьмем произвольный вектор
. Возьмем произвольный вектор  и построим
итерационный процесс
и построим
итерационный процесс 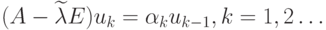 Доказано, что с
увеличением k векторы
Доказано, что с
увеличением k векторы 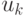 сходятся к вектору
сходятся к вектору  , причем сходимость тем
быстрее, чем ближе
, причем сходимость тем
быстрее, чем ближе 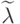 к
к  . Данный метод получил название метода обратных итераций. Но чем ближе
. Данный метод получил название метода обратных итераций. Но чем ближе 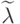 к
к  ,
тем более плохо обусловленной становится матрица
,
тем более плохо обусловленной становится матрица  .
Поэтому из-за ошибок округления при решении
систем уравнений
.
Поэтому из-за ошибок округления при решении
систем уравнений 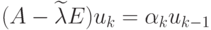 очередной реально найденный вектор
очередной реально найденный вектор 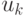 будет содержать очень большие погрешности. Кажется, что по этой
причине метод обратных итераций должен быть несостоятельным на
практике. Однако в действительности он устроен таким образом, что чем
больше погрешность в векторе
будет содержать очень большие погрешности. Кажется, что по этой
причине метод обратных итераций должен быть несостоятельным на
практике. Однако в действительности он устроен таким образом, что чем
больше погрешность в векторе 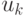 , тем ближе сам вектор погрешности к
искомому вектору
, тем ближе сам вектор погрешности к
искомому вектору  . Другими словами, чем хуже решается система
уравнений из-за влияния ошибок округления, тем лучше сходится
итерационный процесс.
. Другими словами, чем хуже решается система
уравнений из-за влияния ошибок округления, тем лучше сходится
итерационный процесс.
На этом заканчивается наше краткое знакомство с ошибками округления в вычислительных процессах. Мы надеемся, что приведенное описание основ их распределения поможет лучше ориентироваться в алгоритмах вычислительной математики, причем независимо от того, реализуются ли они на последовательных или параллельных компьютерах.
