| Россия |
Конечные автоматы: преобразователи и распознаватели
Этап 1. Устранение пустых переходов.
Рассмотрим поддиаграму автомата M, в которой оставлены лишь ребра, помеченные 
 , где
, где  .
.
Пусть 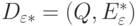 - это граф достижимости (транзитивного замыкания)
для
- это граф достижимости (транзитивного замыкания)
для  . Тогда
. Тогда 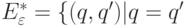 или в
или в  имеется путь из q в q'}.
имеется путь из q в q'}.
Определим НКА  следующим образом:
следующим образом:  , т.е. кроме начального остаются лишь те состояния, в которые
входят "непустые" ребра.
, т.е. кроме начального остаются лишь те состояния, в которые
входят "непустые" ребра.  ,
т.е. к заключительным состояниям M добавляются состояния, из которых можно было
попасть в заключительные по путям из
,
т.е. к заключительным состояниям M добавляются состояния, из которых можно было
попасть в заключительные по путям из  -ребер.
-ребер.
Для каждой пары 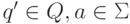 полагаем
полагаем  , т.е. в DM1} имеется a -ребро из q в r, если в DM был (возможно пустой) путь из
, т.е. в DM1} имеется a -ребро из q в r, если в DM был (возможно пустой) путь из  -ребер в некоторое состояние q', из которого a -ребро шло в r.
-ребер в некоторое состояние q', из которого a -ребро шло в r.
Из этого определения непосредственно следует, что в НКА M1 нет пустых переходов
по 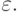 Установим эквивалентность M и M1.
Установим эквивалентность M и M1.
Лемма 4.1.  .
.
Доказательство. Пусть w=w1w2... wt - произвольное входное слово.
Предположим, что  . Это означает, что в диаграмме
. Это означает, что в диаграмме  имеется путь p=e1e2 ... et (e1= (q0=r0,r1), ei=(ri-1,ri), i=2,..., t)
из q0 в некоторое состояние
имеется путь p=e1e2 ... et (e1= (q0=r0,r1), ei=(ri-1,ri), i=2,..., t)
из q0 в некоторое состояние  ,
который несет слово w, т.е. ребро ei помечено символом wi.
Из определения функции
,
который несет слово w, т.е. ребро ei помечено символом wi.
Из определения функции 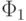 непосредственно следует,
что для любого ребра ei(ri-1, ri) этого пути в диаграмме DM
имеется путь из ri-1 в ri, начало (возможно пустое) которого состоит
из
непосредственно следует,
что для любого ребра ei(ri-1, ri) этого пути в диаграмме DM
имеется путь из ri-1 в ri, начало (возможно пустое) которого состоит
из  -ребер, а последнее ребро помечено символом wi. Объединив эти пути,
получим в диаграмме DM путь из q0 в rt , который несет слово w.
Так как
-ребер, а последнее ребро помечено символом wi. Объединив эти пути,
получим в диаграмме DM путь из q0 в rt , который несет слово w.
Так как  , то либо
, то либо  , либо в DM имеется путь по
, либо в DM имеется путь по  -ребрам из rt в некоторое состояние
-ребрам из rt в некоторое состояние  . В обоих случаях
в DM имеется путь из q0 в заключительное состояние, который несет слово w,
и следовательно,
. В обоих случаях
в DM имеется путь из q0 в заключительное состояние, который несет слово w,
и следовательно, 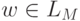 .
.
Обратно, пусть 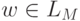 . Тогда в DM имеется путь из q0 в
некоторое заключительное состояние r, который несет слово w. Пусть r0=q0, а ri - это состояние этого пути, в которое приводит ребро с меткой wi (i= 1,... , t).
Рассмотрим отрезок этого пути между вершинами r_{i-1} и ri. Последнее ребро этого отрезка
имеет метку wi, а все предыдущие (если они имеются) помечены
. Тогда в DM имеется путь из q0 в
некоторое заключительное состояние r, который несет слово w. Пусть r0=q0, а ri - это состояние этого пути, в которое приводит ребро с меткой wi (i= 1,... , t).
Рассмотрим отрезок этого пути между вершинами r_{i-1} и ri. Последнее ребро этого отрезка
имеет метку wi, а все предыдущие (если они имеются) помечены 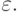 Тогда по определению
Тогда по определению 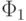 в диаграмме
в диаграмме  между r_{i-1} и ri
имеется ребро с меткой wi. Объединив эти ребра, получим в
между r_{i-1} и ri
имеется ребро с меткой wi. Объединив эти ребра, получим в  путь
из q0 в rt. Так как либо
путь
из q0 в rt. Так как либо 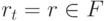 , либо в DM из rt имеется
путь из
, либо в DM из rt имеется
путь из  -ребер в
-ребер в 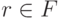 , то из определения F1 следует, что
, то из определения F1 следует, что  .
Таким образом,
.
Таким образом,  .
.
Этап 2. Детерминизация.
Идея детерминизации состоит в том, что состояниями ДКА объявляются подмножества состояний НКА. Тогда для каждого такого подмножества T и входного символа a однозначно определено множество состояний T', в которые НКА может попасть из состояний T при чтении a.
Определим по НКА  ДКА
ДКА  следующим образом.
следующим образом.

Ясно, что A - детерминированный конечный автомат. Следующая лемма устанавливает связь между его вычислениями и вычислениями исходного НКА.
Лемма 4.4. Для любой пары состояний Q', Q'' из QA и любого слова 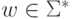 имеем
имеем
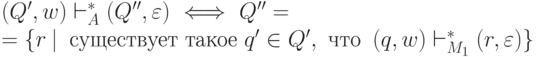
Доказательство. Применим индукцию по длине слова w.
Базис. Пусть |w|=0, тогда 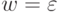 , Q' = Q'' и утверждение выполнено.
Пусть теперь |w|=1 и
, Q' = Q'' и утверждение выполнено.
Пусть теперь |w|=1 и 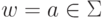 . Тогда утверждение леммы следует непосредственно
из определения
. Тогда утверждение леммы следует непосредственно
из определения  .
.
Шаг индукции. Предположим, что лемма справедлива для всех слов длины <= k,
и пусть |w| = k+1. Выделим в w первый символ: w=aw'.
Пусть 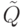 - это такое состояние, что
- это такое состояние, что 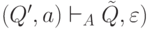 .
Тогда
.
Тогда  .
Так как |w'|=k, то по индукционному предположению это эквивалентно
следующему:
.
Так как |w'|=k, то по индукционному предположению это эквивалентно
следующему:  .
Но из определения
.
Но из определения  следует, что
следует, что 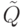
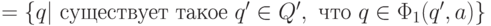 .
Объединив, эти два равенства, получаем:
.
Объединив, эти два равенства, получаем:  .
.
Для завершения доказательства теоремы покажем с помощью
леммы 4.4, что 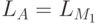 .
.
Действительно, если слово w переводит состояние q0 в некоторое 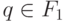 в автомате M1, то, положив в лемме Q' ={ q0}, получим, что
в автомате M1, то, положив в лемме Q' ={ q0}, получим, что  для состояния Q'', такого, что
для состояния Q'', такого, что  . Но тогда
. Но тогда  и
и  .
.
Обратно, если  , то для некоторого
, то для некоторого  имеем
имеем  . Тогда в Q''
имеется некоторое состояние
. Тогда в Q''
имеется некоторое состояние 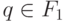 и по лемме 4.4 в автомате
и по лемме 4.4 в автомате 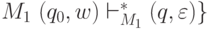 , т.е.
, т.е.  .
.
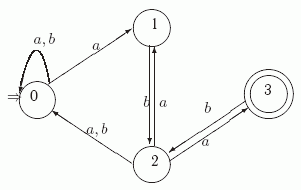
Пример 4.2. Применим процедуру из теоремы о детерминизации к НКА N1 из примера 4.3.
На первом этапе получаем  и
НКА M1 без пустых переходов, представленный на следующей диаграмме.
и
НКА M1 без пустых переходов, представленный на следующей диаграмме.
Заметим, что состояние 4 исчезло, так как в автомате N1 в него можно было
попасть только по  -переходу.
-переходу.
На втором этапе детерминизируем M1. ДКА A будет иметь 16 состояний: 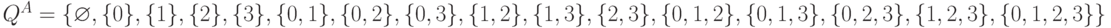 .
.
Во множество заключительных состояний войдут состояния, содержащие заключительное состояние 3 автомата M1:
F^A={{3},{0,3}, {1,3}, {0,1,3}, {0,2,3},{1,2,3}, {0,1,2, 3}}.
Функция переходов  определена в следующей таблице
определена в следующей таблице
 |
a | b |
|---|---|---|
hline 
|
 |
 |
| {0} | {0,1} | {0} |
| {1} |  |
{2} |
| {2} | {0,1,3} | {0} |
| {3} |  |
{2} |
| {0,1} | {0,1} | {0,2} |
| {0,2} | {0,1,3} | {0} |
| {0,3} | {0,1} | {0,3} |
 |
a | b |
|---|---|---|
| {1,2} | {0,1,3} | {0,2} |
| {1,3} |  |
{2} |
| {2,3} | {0,1,3} | {0,2} |
| {0,1,2} | {0,1,3} | {0,2} |
| {0,1,3} | {0,1} | {0,2} |
| {0,2,3} | {0,1,3} | {0,2} |
| {1,2,3} | {0,1,3} | {0,2} |
| {0,1,2,3} | {0,1,3} | {0,2} |
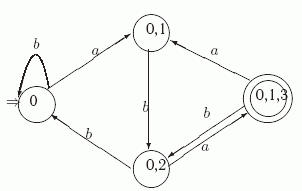
На самом деле нас интересуют лишь те состояния, в которые можно попасть из начального состояния {0}. Несложный анализ показывает, что их только три: {0,1}, {0,2 } и {0, 1, 3 }. Остальные состояния не достижимы из {0} и, следовательно, не влияют на работу автомата A. Их можно отбросить. Таким образом, в диаграмме автомата остаются 4 состояния, показанные на рис. 4.5.
Замечание. В рассмотренном примере у построенного ДКА A оказалось не больше состояний, чем у исходного НКА N1. К сожалению, это не всегда так. Существуют примеры НКА с n состояниями, для которых эквивалентные ДКА содержат не менее 2n состояний.
Задачи
Задача 4.1. Автомат по продаже кофе имеет щель для получения монет, кнопку, нажатие которой после уплаты достаточной суммы приводит к получению кофе, и накопитель, через который он выдает сдачу покупателю. Автомат принимает монеты достоинством в 1, 2 и 5 рублей. Чашка кофе стоит 8 руб. Пока полученная сумма недостаточна, горит красная лампочка. Если сумма, полученная автоматом, >= 8, то зажигается зеленая лампочка и после нажатия кнопки автомат наливает кофе и, если требуется, дает сдачу. Если автомат получает монету, когда горит зеленая лампочка, то он немедленно ее возвращает. Определите входной и выходной алфавиты конечного автомата, управляющего продажей кофе, и постройте его функции переходов и выходов.
Задача 4.2. Электронные часы имеют табло с указанием часов, минут и секунд и две управляющие кнопки. Одна кнопка переводит часы из нормального режима в режим настройки времени - вначале в настройку часов, затем - минут, затем - секунд, а затем возвращает в нормальный режим. Другая кнопка в нормальном режиме ничего не меняет, а в режиме настройки нажатие на нее увеличивает на единицу число настраеваемых часов, минут или секунд. Постройте автомат, который принимает на вход сигналы нажатия от двух кнопок, а на выходе выдает сигналы изменения режима и увеличения соответствующего числа.
Задача 4.3. Докажите лемму 4.1 индукцией по длине входного слова.
Задача 4.4. Постройте детерминированные конечные автоматы, которые
распознают следующие языки в алфавите  :
:
- L = {w | длина w делится на 5} ;
- L = {w | w не содержит подслов 'aab' и 'bba'} ;
- L = {w | w содержит четное число букв а и нечетное число букв b} ;
- L = {w | число букв а делится на 3, а число букв b на 2 }.
Задача 4.5. Выше в примере 4.1 был построен автомат с выходом, выполняющий сложение двух двоичных чисел. Постройте автомат-распознаватель, который проверяет правильность сложения. На вход поступают последовательности троек нулей и единиц:

Автомат должен допустить такую последовательность, если y = y(n) ... y(2)y(1) - это первые n битов суммы двоичных чисел x1= x1(n)... x1(2)x1(1) и x2 = x2(n)... x2(2)x2(1).
Задача 4.7. Докажите лемму 4.2.
Задача 4.8. Докажите, что приведенный на рис. 4.5 автомат A распознает язык, состоящий из всех слов, заканчивающихся на 'aba'.
Задача 4.9. Используя процедуру детерминизации недетерминированных автоматов из теоремы 4.2, постройте ДКА, эквивалентный заданному НКА M.
-
 с программой
с программой 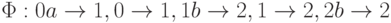 .
. -
 с программой
с программой 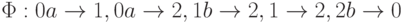 .
.