НОУ ИНТУИТ | Введение в схемы, автоматы и алгоритмы. Лекция 2: Реализация булевых функций с помощью логических схем

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 21.08.2007 | Уровень: специалист | Доступ: платный | ВУЗ: Тверской государственный университет

|

Вам нравится? Нравится 36 студентам

| Поделиться |

Поддержать программу

Примеры схем

Сложение по модулю 2

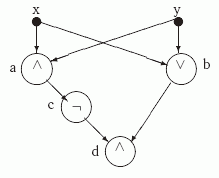
Рассмотрим схему S₊ на рис. 2.2.

Рис. 2.2. Схема S+ для функции x+y

В соответствии с определением вершины этой схемы реализуют следующие функции:

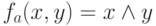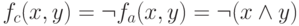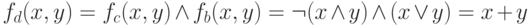$f_{a}(x,y) = x \wedge y$ , $f_{b}(x,y) = x \vee y$ , $f_{c}(x,y) = \neg f_{a}(x,y)=\neg ( x \wedge y)$ , $f_{d}(x,y) = f_{c}(x,y) \wedge f_{b}(x,y) = \neg ( x \wedge y) \wedge ( x \vee y) = x +y$ .

Таким образом, схема S₊ реализует (в вершине d ) функцию + сложения по модулю 2.

Из приведенного выше примера следует, что L(S₊)=4 и L(+) <= 4.

Используя схему S₊, нетрудно построить схему S_odd для реализации линейной функции-суммы n аргументов по модулю 2 odd(X₁,X₂,..., X_n)= X₁ +X₂ +... + X_n (см. рис. 2.3).

Рис. 2.3. Схема Sodd

На этой схеме прямоугольники S₊⁽¹⁾, S₊⁽²⁾, ... ,S₊⁽ⁿ⁾ содержат копии схемы S₊. При этом входами S₊⁽¹⁾ являются переменные x₁ и x₂, а входами S₊⁽ⁱ⁺¹⁾ являются выход схемы S₊⁽ⁱ⁾ и переменная x_i+1. По индукции легко показать, что вершина d в S₊⁽ⁱ⁾ реализует функцию (x₁ + x₂ + ... + x_i+1). Таким образом, нами установлена

Теорема 2.2. Существует схема S_odd, реализующая функцию odd(X₁,X₂,..., X_n)= X₁ +X₂ +... + X_n со сложностью L(S_odd)= 4 (n-1).

Сумматор

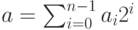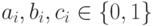Сумматором порядка n называют схему, вычисляющую результат сложения двух n -разрядных двоичных чисел $a = \sum_{i=0}^{n-1} a_i 2^i$ и $b = \sum_{i=0}^{n-1} b_i 2^i$ . Пусть $c= a+b = \sum_{i=0}^{n} c_i 2^i$ ( здесь $a_{i}, b_{i}, c_{i} \in \{ 0, 1\}$ - соответствующие двоичные разряды этих чисел).

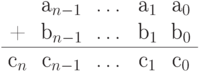
$\begin{tabular}{ccccc} & a_{n-1} & \ldots & a_1& a_0\\ +& b_{n-1} & \ldots & b_1& b_0\\ \hline c_n & c_{n-1} & \ldots & c_1& c_0 \end{tabular}$

Сумматор должен вычислять набор из (n+1) -ой результирующей функции:

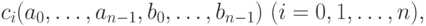
$c_i(a_0,\ldots,a_{n-1}, b_0,\ldots, b_{n-1})\ (i=0,1, \ldots , n),$

задающих соответствующие разряды суммы c.

Обозначим через p_i бит переноса из (i-1) -го разряда в i -ый. Тогда нетрудно видеть, что при i =0

c₀ = a₀ + b₀ и 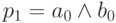$p_{1} = a_{0} \wedge b_{0}$ ,

а при 1 <= i <= n-1

c_i= p_i + a_i + b_i и 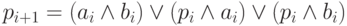$p_{i+1} = (a_{i} \wedge b_{i}) \vee (p_{i} \wedge a_{i}) \vee (p_{i} \wedge b_{i})$ .

Старший разряд c совпадает с последним переносом: c_n=p_n.

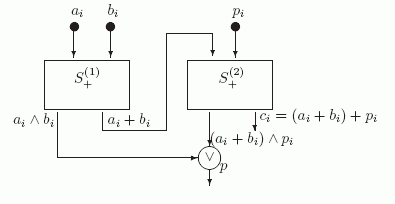
Рассмотрим теперь построенную выше схему S₊ как схему, вычисляющую набор из двух функций: 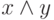$x \wedge y$ (в вершине a ) и x+y (в вершине d ). Используя два экземпляра этой схемы S₊⁽¹⁾ и S₊⁽²⁾, можно легко реализовать схему одноразрядного сумматора SUM₁ (см. рис. 2.4) , которая имеет три входа a_i, b_ i и p_i ( 1 <= i <= n-1 ) и вычисляет c_i и p_i+1.

Рис. 2.4. Схема SUM1

Действительно, из построения следует, что в вершине p этой схемы вычисляется функция 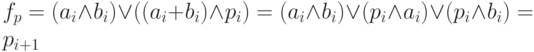$f_{p} = (a_{i} \wedge b_{i}) \vee ((a_{i} + b_{i}) \wedge p_{i}) =(a_{i} \wedge b_{i}) \vee (p_{i} \wedge a_{i}) \vee (p_{i} \wedge b_{i}) = p_{i+1}$ . Из представленной схемы видно, что сложность одноразрядного сумматора L(SUM₁)= 9.

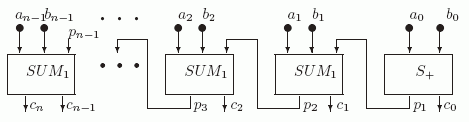
Теперь из S₊ и одноразрядных сумматоров SUM₁ соберем схему SUM_n для n -разрядного сумматора.

Рис. 2.5. Схема cумматора SUMn

Таким образом мы установили следующее утверждение.

Теорема 2.3.

Для каждого n >= 1 cуществует схема SUM, реализующая операцию суммирования двух n -разрядных двоичных чисел и имеющая сложность L(SUM_n)= 9n -5.

Замечание Логические схемы интенсивно исследовались 50-х-70-х годах прошлого столетия. В частности, К. Шеннон и О.Б. Лупанов установили оценки сложности схем для булевых функций от n аргументов. Оказалось, что любую такую функцию можно реализовать со сложностью не большей (по порядку) 2ⁿ/n и что "почти все" они имеют не меньшую сложность. При этом до сих пор не известна ни одна последовательность "конкретных" функций f_n, сложность которых по порядку превосходила бы линейную функцию.

Задачи

Задача 2.1. Докажите пункт (2) теоремы 2.1.

Задача 2.2. Докажите, что минимальная схема для сложения имеет сложность L(+) = 4.

Задача 2.3. Используя схему SUM_n, постройте схему, реализующую операцию вычитания двух n -разрядных двоичных чисел: d =a - b (при условии, что a >= b ). Оцените сложность полученной схемы.

Задача 2.4. Определите глубину схем S₊, S_odd, SUM₁ и SUM_n.

Задача 2.5. Два игрока независимо выбирают одно из четырех чисел от 0 до 3. Первый игрок выигрывает, если выбранные числа совпадают. Постройте схему, определяющую выигрыш 1-го игрока. Ее входы x₁,x₂ представляют число, выбранное 1-ым игроком, а y₁,y₂ - число, выбранное 2-ым игроком. Реализуемая функция F(x₁,x₂,y₁,y₂) равна 1 тогда и только тогда, когда x₁=y₁ и x₂ =y₂.

Задача 2.6. Постройте схему, определяющую результат голосования в комитете, состоящем из трех членов и председателя. В случае равенства голосов, голос председателя является решающим.

Задача 2.7. Пусть наборы аргументов булевой функции от трех аргументов упорядочены лексикографически, а ее значения задаются последовательностью 8 нулей и единиц. Постройте схемы, реализующие следующие функции.

f₁=(1111 1011),
f₂=(1001 1001),
f₃ =(0011 1001).

Дальше >>

Введение в схемы, автоматы и алгоритмы

Введение в схемы, автоматы и алгоритмы