Базисные средства манипулирования реляционными данными: реляционная алгебра Кодда

Операция соединения отношений

Общая операция соединения (называемая также соединением по условию) требует наличия двух операндов – соединяемых отношений и третьего операнда – простого условия. Пусть соединяются отношения A и B. Как и в случае операции ограничения, условие соединения comp имеет вид либо ( a comp-op b ), либо ( a comp-op const ), где a и b – имена атрибутов отношений A и B, const – литерально заданная константа, и comp-op – допустимая в данном контексте операция сравнения.

Тогда по определению результатом операции соединения A JOIN B WHERE comp совместимых по взятию расширенного декартова произведения отношений A и B является отношение, получаемое путем выполнения операции ограничения по условию comp расширенного декартова произведения отношений A и B .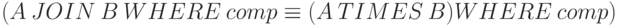

Если тщательно осмыслить это определение, то станет ясно, что в общем случае применение условия соединения существенно уменьшит мощность результата промежуточного декартова произведения отношений-операндов только в том случае, если условие соединения имеет вид ( a comp-op b ), где a и b – имена атрибутов разных отношений-операндов. Поэтому на практике обычно считают реальными операциями соединения именно те операции, которые основываются на условии соединения приведенного вида.

В подразделе, касающемся операции ограничения, мы определили трактовку использования в качестве ограничивающего условия произвольного булевского выражения, которое составлено из простых условий над атрибутами отношения-операнда и литеральными константами. Конечно же, и в операции соединения может задаваться произвольное логическое выражение, составленное из простых условий над атрибутами отношений-операндов и константами. Операцию соединения с таким условием comp разумно считать операцией действительного соединения, если оно имеет вид (или может быть преобразовано к виду) comp1 AND (a comp-op b), где a и b – имена атрибутов разных отношений-операндов.

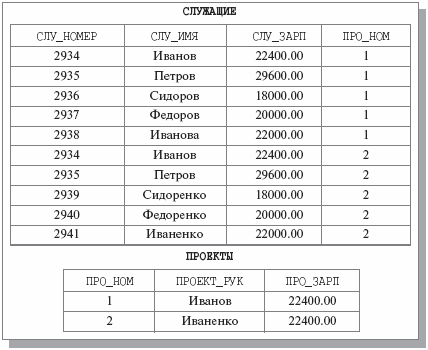
Для иллюстрации операций соединения мы немного изменим заголовки и тела отношений, которые использовались ранее в примерах этой лекции. Пусть теперь имеются отношения СЛУЖАЩИЕ {СЛУ_НОМЕР, СЛУ_ИМЯ, СЛУ_ЗАРП, ПРО_НОМ} (атрибут ПРО_НОМ содержит номера проектов, в которых участвует каждый служащий) и ПРОЕКТЫ {ПРО_НОМ, ПРОЕКТ_РУК, ПРО_ЗАРП} ( ПРО_НОМ – номер проекта, ПРОЕКТ_РУК – имя служащего-руководителя проекта, ПРО_ЗАРП – средняя заработная плата служащих, участвующих в проекте). Примерное содержимое тел отношений СЛУЖАЩИЕ и ПРОЕКТЫ показано на рис. 3.8.

Тогда осмысленной операцией соединения общего вида будет СЛУЖАЩИЕ JOIN ПРОЕКТЫ WHERE (СЛУ_ЗАРП > ПРО_ЗАРП) (выдать данные о служащих, получающих заработную плату, превышающую среднюю заработную плату любого проекта). Результаты этого запроса показаны на рис. 3.9.

Хотя операция соединения в приведенной интерпретации не является примитивной (поскольку определяется с использованием операций декартова произведения и проекции ), в силу особой практической важности она включается в базовый набор операций реляционной алгебры Кодда. Заметим также, что в практических реализациях соединение обычно не выполняется именно как ограничение декартова произведения. Имеются более эффективные алгоритмы, гарантирующие получение такого же результата.

Существует важный частный случай соединения – эквисоединение ( EQUIJOIN ) и простое, но важное расширение операции эквисоединения – естественное соединение ( NATURAL JOIN ). Операция соединения называется операцией эквисоединения, если условие соединения имеет вид ( a = b ), где a и b – атрибуты разных операндов соединения. Этот случай важен потому, что он чаще всего встречается на практике, и для него существуют наиболее эффективные алгоритмы реализации.

Рис. 3.8. Отношения СЛУЖАЩИЕ и ПРОЕКТЫ

Операция естественного соединения применяется к паре отношений A и B, обладающих (возможно, составным) общим атрибутом c (т. е. атрибутом с одним и тем же именем и определенным на одном и том же домене). Пусть ab обозначает объединение заголовков отношений A и B. Тогда естественное соединение A и B – это спроецированный на ab результат эквисоединения A и B по условию A.c = B.c^{2Здесь A.c и B.c представляют собой так называемые квалифицированные (уточненные) имена атрибутов (часто такой способ именования называют точечной нотацией). Мы будем использовать подобную нотацию в тех случаях, когда требуется явно показать, схеме какого отношения принадлежит данный атрибут.} . Хотя операция естественного соединения выражается через операции переименования, соединения общего вида и проекции, для нее обычно используется сокращенная форма, называемая NATURAL JOIN.

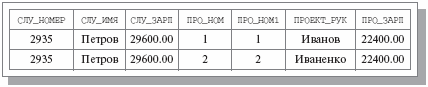
На рис. 3.10 приведены результаты операций СЛУЖАЩИЕ JOIN (ПРОЕКТЫ RENAME (ПРО_НОМ, ПРО_НОМ1)) WHERE (СЛУ_ЗАРП = ПРО_ЗАРП) ( эквисоединение отношений СЛУЖАЩИЕ и ПРОЕКТЫ: найти всех служащих, получающих зарплату, равную средней заработной плате в каком-либо проекте) и СЛУЖАЩИЕ NATURAL JOIN ПРОЕКТЫ ( естественное соединение – выдать полную информацию о служащих и проектах, в которых они участвуют).

Рис. 3.9. Результат операции СЛУЖАЩИЕ JOIN ПРОЕКТЫ WHERE (СЛУ_ЗАРП > ПРО_ЗАРП)

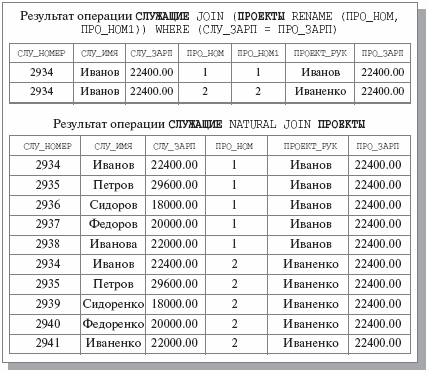
Рис. 3.10. Результаты операций эквисоединения и естественного соединения отношений СЛУЖАЩИЕ и ПРОЕКТЫ

Если вспомнить введенное нами в конце предыдущей лекции определение внешнего ключа отношения, то должно стать понятно, что основной смысл операции естественного соединения состоит в возможности восстановления сложной сущности, декомпозированной по причине требования первой нормальной формы. Операция естественного соединения не включается в состав набора операций данной реляционной алгебры Кодда, но имеет очень важное практическое значение.

Операция деления отношений

Эта операция наименее очевидна из всех операций реляционной алгебры Кодда и поэтому нуждается в более подробном объяснении. Пусть заданы два отношения – A с заголовком {a₁, a₂, ..., a_n, b₁, b₂, ..., b_m} и B с заголовком {b₁, b₂, ..., b_m}. Будем считать, что атрибут b_i отношения A и атрибут b_i отношения B (i = 1, 2, …, m) не только обладают одним и тем же именем, но и определены на одном и том же домене. Назовем множество атрибутов {a_j} составным атрибутом a, а множество атрибутов {b_j} – составным атрибутом b. После этого будем говорить о реляционном делении "бинарного" отношения A{a, b} на унарное отношение B{b}.

По определению, результатом деления A на B (A DIVIDE BY B) является "унарное" отношение C{a}, тело которого состоит из кортежей v таких, что в теле отношения A содержатся кортежи v UNION w такие, что множество {w} включает тело отношения B. Операция реляционного деления не является примитивной и выражается через операции декартова произведения, взятия разности и проекции. Мы покажем это в следующей лекции.

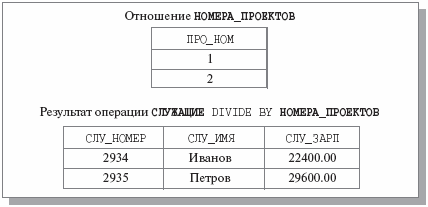
Для иллюстрации этой операции предположим, что в базе данных служащих поддерживаются следующие отношения: СЛУЖАЩИЕ, как оно было определено ранее, и унарное отношение НОМЕРА_ПРОЕКТОВ {ПРО_НОМ} (рис. 3.11). Тогда запрос СЛУЖАЩИЕ DIVIDE BY НОМЕРА_ПРОЕКТОВ выдаст данные обо всех служащих, участвующих во всех проектах (результат операции приведен также на рис. 3.11).

Рис. 3.11. Пример реляционного деления

Заключение

В завершение лекции хочу отметить несколько моментов. Прежде всего, заметим, что алгебра Кодда была представлена не в ее оригинальной форме, а с некоторыми существенными коррективами, внесенными Кристофером Дейтом. С моей точки зрения, одной из наиболее значительных корректив было добавление тривиальной на первый взгляд операции переименования атрибутов. Когда Эдгар Кодд в конце 1960-х гг. впервые опубликовал свою алгебру, основное внимание в ней уделялось тому, как конструируются результирующие множества кортежей, т. е. что представляют собой тела результатов операций. Гораздо меньше внимания уделялось заголовкам отношений-результатов. Фактически Кодд пытался применить для именования атрибутов результатов операций точечную нотацию, используя для уточнения имен атрибутов имена исходных отношений-операндов. При наличии произвольно сложных и длинных алгебраических выражений этот путь, в лучшем случае, вел к порождению длинных и трудных для восприятия имен. Очевидно, что введение операции переименования атрибутов позволяет легко справиться с этой проблемой.

Далее, алгебра Кодда исключительно избыточна. Операции пересечения, декартова произведения и естественного соединения, на самом деле, являются частными случаями одной более общей операции, о которой пойдет речь в следующей лекции. Введение операции декартова произведения в качестве базовой операции алгебры может ввести в заблуждение неопытных студентов и читателей, не осознающих практическую бессмысленность этой операции.

Почему же мы начали обсуждение базовых манипуляционных механизмов реляционной модели данных с этой небезупречной и несколько устаревшей алгебры? Конечно, прежде всего, из уважения к заслугам доктора Эдгара Кодда, вклад которого в современную технологию баз данных невозможно переоценить. Более практические соображения, повлиявшие на наше решение начать обсуждение с алгебры Кодда, заключались в том, что семантика языка SQL во многом базируется именно на этой алгебре, и нам будет проще изучать SQL, предварительно познакомившись с ней.