| Россия, Волгоградская область |
Роевые и муравьиные алгоритмы
11.4. Основные параметры роевых алгоритмов
Эффективность РА зависит от ряда параметров, к которым относятся: размерность задачи, число частиц, коэффициенты ускорения, вес инерции, тип и размер соседнего окружения, число итераций, кооэффициенты, определяющие вклад когнитивной и социальной компонент. В случае наложения ограничений на возможные скорости частиц необходимо также определить максимальне значения и некоторые коэффициенты. Далее рассмотрим основне параметры РА.
Размер роя, число частиц  , играет большую роль: чем больше частиц, тем больше разнообразие потенциальных решений (при хорошей схеме инициализации, обеспечивающей однородное распределение частиц). Большое число частиц позволяет покрыть большую часть пространства поиска за итерацию. С другой стороны большое число частиц повышает вычислительную сложность итерации и при этом РА может выродиться в случайный параллельный поиск. Хотя бывают случаи, что большее число частиц ведет к уменьшению числа итераций при поиске хороших решений. Экспериментально показано, что РА способны находить оптимальное решение с малым размером роя от 10 до 30 частиц [3]. В общем случае оптимальный размер роя зависит от решаемой задачи и определяется экспериментально.
, играет большую роль: чем больше частиц, тем больше разнообразие потенциальных решений (при хорошей схеме инициализации, обеспечивающей однородное распределение частиц). Большое число частиц позволяет покрыть большую часть пространства поиска за итерацию. С другой стороны большое число частиц повышает вычислительную сложность итерации и при этом РА может выродиться в случайный параллельный поиск. Хотя бывают случаи, что большее число частиц ведет к уменьшению числа итераций при поиске хороших решений. Экспериментально показано, что РА способны находить оптимальное решение с малым размером роя от 10 до 30 частиц [3]. В общем случае оптимальный размер роя зависит от решаемой задачи и определяется экспериментально.
Размер соседнего окружения определяет степень влияния социальной компоненты в локальных РА. Чем меньше соседей у частицы, тем меньше ее взаимодействие с окружением. Малый размер определяет малую скорость сходимости, но дает большую надежность поиска оптимума. Чем меньше размер окружения, тем меньше чувствительность к локальным экстремумам. Для использования преимуществ малого и большого размера окружения часто стартуют с малым размером соседней окрестности и далее в процессе поиска размер окружения увеличивают пропорционально числу выполненных итераций. Такой подход обеспечивает хорошее начальное разнообразие и быструю сходимость частиц к перспективной области поиска.
Число итераций, обеспечивающее нахождение хорошего решения, зависит от решаемой задачи. При малом числе процесс поиска может не успеть сойтись. С другой стороны, большое число итераций, естественно, повышает вычислительную сложность.
Коэффициенты ускорения 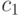 и
и 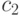 вместе со случайными векторами
вместе со случайными векторами 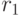 и
и 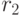 определяют вклад когнитивной и социальной компонент в результирующую скорость частицы. При
определяют вклад когнитивной и социальной компонент в результирующую скорость частицы. При 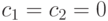 частицы летают с прежней скоростью пока не достигнут (по инерции) границы пространства поиска. Если
частицы летают с прежней скоростью пока не достигнут (по инерции) границы пространства поиска. Если  и
и 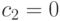 , частица не зависит от остальных особей. Каждая частица находит свою лучшую позицию в своем окружении путем замены лучшей позиции в том случае, если текущая позиция лучше. В случае
, частица не зависит от остальных особей. Каждая частица находит свою лучшую позицию в своем окружении путем замены лучшей позиции в том случае, если текущая позиция лучше. В случае  и
и  , весь рой стремится к одной точке
, весь рой стремится к одной точке  . Эксперименты показывают, что эффективность поиска увеличивается при балансе этих коэффициентов, т.е. при
. Эксперименты показывают, что эффективность поиска увеличивается при балансе этих коэффициентов, т.е. при 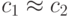 . Если
. Если  , то частицы стремятся к средней точке между
, то частицы стремятся к средней точке между  и
и  . Часто при решении задач полагают
. Часто при решении задач полагают  , но в общем случае отношение этих коэффициентов зависит от решаемой задачи. При
, но в общем случае отношение этих коэффициентов зависит от решаемой задачи. При  каждая частица больше стремится к своей лучшей позиции, что в результате ведет к чрезмерному блужданию частиц. Наоборот
каждая частица больше стремится к своей лучшей позиции, что в результате ведет к чрезмерному блужданию частиц. Наоборот  определяет большее стремление частиц к глобальному экстремуму. Обычно значения
определяет большее стремление частиц к глобальному экстремуму. Обычно значения  в процессе поиска постоянны, но иногда используются адаптивные схемы, когда величины
в процессе поиска постоянны, но иногда используются адаптивные схемы, когда величины  изменяются [3].
изменяются [3].
