Роевые и муравьиные алгоритмы

11.3. Основные аспекты роевых алгоритмов

Далее рассмотрим некоторые аспекты представленных выше роевых алгоритмов А11.1 и А11.2, к которым относятся вопросы инициализации, условий останова, вычисления фитнесс-функций и т.п. Как было показано ранее, процесс поиска решения в РА согласно А 11.1 и А 11.2 является итеративным, который продолжается пока не выполнено условие останова. Одна итерация содержит все шаги основного цикла repeat …until, включая определение персональных и глобальных лучших позиций и коррекцию скорости каждой частицы. В каждой итерации производится оценка значений фитнесс-функций частиц. Оценка качества потенциального решения выполняется на основе вычисления значения фитнесс-функции, которая характеризует данную задачу оптимизации. В основном РА выполняется вычислений фитнесс-функции за итерацию, где - число частиц в рое.

На первом этапе РА производится инициализация роя и управляющих параметров алгоритма. При этом определяются начальные значения скоростей, позиций и персональных лучших позиций частиц, коэффициенты ускорения 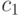, 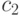и т.п. Для локальных РА необходимо также определить отношение соседства и размер окрестности ближайших соседей.

Обычно позиции частиц инициализируются таким образом, чтобы пространство поиска покрывалось равномерно. Следует отметить, что эффективность РА существенно зависит от начального разнообразия множества потенциальных решений, то есть от того, как первоначально покрыто пространство поиска и как распределены частицы в нем. Если некоторые области пространства поиска не покрыты начальным роем, то РА будет трудно найти оптимум в том случае, когда он расположен в не охваченном участке. В этом случае РА может найти такой оптимум благодаря моменту частицы, который может направить ее в неисследованную область.

Предположим, что оптимум расположен внутри области, определяемой двумя векторами 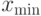, , которые представляют минимальные и максимальные значения по каждой координате. Тогда эффективным методом инициализации начальной позиции частиц является:

( 11.8)

где .

Начальные скорости частиц при этом можно положить нулевыми . В другом варианте начальные скорости можно инициализировать случайными значениями из некоторого диапазона, но делать это необходимо осторожно. Случайная инициализация позиций частиц уже определяет начальное движение в случайных направлениях. Если, однако, выполняется случайная инициализация скоростей, то их значения не должны быть слишком большими, чтобы частицы не вышли из "зоны интереса", что может существенно ухудшить сходимость.

Персональная лучшая позиция для каждой частицы определяется позицией частицы в момент 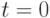, то есть . Различные схемы инициализации позиций частиц исследованы для покрытия пространства поиска [3]: на основе последовательностей Соболя, Faure, нелинейного симплекс-метода и т.д. При решении реальных задач важно, прежде всего, чтобы частицы равномерно покрывали пространство поиска.

Следующий аспект РА касается условия останова процесса поиска решения, где необходимо учитывать следующее:

1. критерий не должен вызывать преждевременной сходимости РА в локальных оптимумах;
2. критерий должен предотвращать чрезмерно большие вычисления вследствие частой оценки фитнесс-функции частиц.

В настоящее время предложен ряд критериев останова, основными из которых являются следующие.

Останов по максимальному числу итераций (при превышении заданного порога). Очевидно, что в случае малого порога числа итераций процесс может остановиться до того, как будет найдено хорошее решение. Это критерий обычно используется совместно с критерием сходимости. Данный критерий полезен, когда необходимо за ограниченное заданное время найти лучшее решение.

Останов по найденному приемлемому решению. Предположим, что 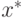представляет оптимум для целевой функции . Тогда критерий окончания можно сформулировать в терминах близости найденного лучшего решения к оптимуму , то есть при достижении достаточно малой ошибки . Значение порога ошибки необходимо выбирать осторожно. Если значение слишком велико, то очевидно процесс поиска может остановиться, если найдено не очень хорошее решение. С другой стороны, если значение слишком мало, то процесс может вовсе не сойтись. Это особенно характерно для основного (глобального) РА. Кроме этого,данный критерий предполагает априорное знание оптимального значения, которое не всегда известно, кроме случаев минимизации ошибки (например, в процессе обучения).

Останов по отсутствию улучшения решения за заданное число итераций. Есть различные способы измерения улучшения получаемых решений. Например, среднее изменение позиции частиц мало, то можно предположить, что процесс поиска сошелся. С другой стороны, если среднее значение скорости частицы за некоторое число итераций примерно равно нулю, то возможны только незначительные изменения позиции частиц и процесс поиска можно остановить. К сожалению, данный критерий требует ввода двух параметров: 1) диапазона изменения итераций, 2) пороговое значение наблюдаемых величин.

Останов при стремлении нормализованного радиуса роя к нулю. Определим нормализованный радиус роя следующим образом:

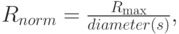( 11.9)

где diameter(S) - диаметр начального роя и максимальный радиус определяется следующим образом

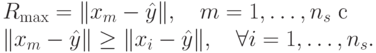
Можно считать, что алгоритм сошелся, если . Если слишком велико, то процесс поиска может закончиться раньше, чем будет найдено хорошее решение. С другой стороны при малом значении может потребоваться слишком большое число итераций для формирования компактного роя.

Останов по малому значению наклона (крутизны) целевой функции.Рассмотренные критерии учитывают только относительное расположение частиц в пространстве поиска и не принимают во внимание информацию о крутизне целевой функции. Для учета изменений целевой функции часто используют следующее отношение:

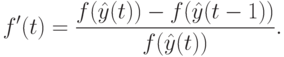( 11.10)

Если для определенного числа последовательных итераций, то можно считать, что рой сошелся. Этот критерий сходимости, по мнению многих специалистов, превосходит приведенные ранее, так как он учитывает динамические характеристики роя. Однако использование крутизны целевой функции в качестве критерия останова может привести к преждевременной сходимости в локальном экстремуме. Поэтому целесообразно использовать данный критерий в сочетании с приведенным ранее критерием нормализованного радиуса роя.

Следует отметить, что сходимость по приведенным критериям, в общем случае, может не соответствовать достижению оптимума (глобального или локального). В данном случае сходимость означает, что рой достиг состояния равновесия, когда частицы стремятся к некоторой точке в пространстве поиска (в общем случае необязательно точке оптимума).