НОУ ИНТУИТ | Эволюционные вычисления. Лекция 9: Эволюционные стратегии

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Твой путь к знаниям!

Опубликован: 10.10.2014 | Уровень: для всех | Доступ: платный | ВУЗ: Московский государственный университет путей сообщения

|

Вам нравится? Нравится 18 студентам

| Поделиться |

Поддержать программу

9.3. Основные параметры и самоадаптация

В ЭС параметры ассоциируются с каждой особью популяции. Обычно для этих параметров производится самоадаптация для определения лучшего направления поиска и максимально возможного шага. По сути, параметры определяют вероятностное распределение, используемое в мутации, из которого определяется размер шага. Основная идея самоадаптации заключается в том, как улучшить распределение мутации, чтобы максимально поддержать сходимость поиска решения.

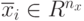В первых реализациях ЭС применялся только один вид параметра – отклонение в распределении Гаусса, которое используется в операторе мутации. В этом случае, как показано в разделе 9.1, –я особь определяется как $v=(\overline x_i,\overline\sigma_i)$ , где $\overline x_i\in R^{n_x}$ представляет генотип и 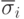$\overline\sigma_i$ - вектор-параметр отклонений (обычно $\overline\sigma_i\in R^{n_x}$ и все компоненты отклонения одинаковы $\sigma_{ij}=\sigma_i$ для $j=1,2,\dots,n_x$ ). Применение большего числа параметров дает больше степеней свободы особям и лучшие возможности для регулирования распределения мутации.

Если в качестве параметров используются только отклонения, то лучшие направления поиска определяются вдоль осей системы координат пространства поиска. Но не всегда лучшее направление поиска совпадает с осями. В таких случаях необходима дополнительная информация для ускорения процесса сходимости. Такую информацию можно получить из матрицы – гессиана фитнесс-функции. Если гессиан используется в качестве параметра, то мутация определяется следующим образом:

$x_i(t)=x_i(t)+N(0,H^{-1}).$

К сожалению, не всегда можно использовать гессиан, поскольку фитнесс-функции не гарантируют существование производных второго порядка. Но даже если эти производные существуют, то построение гессиана имеет значительную вычислительную сложность. Потому разработаны и другие методы.

В [4] предложено использовать матрицу ковариации $C^{-1}$ , которая определяется отклонениями параметров особи и может использоваться в качестве дополнительной информации, позволяющей определить оптимальный размер шага и направление поиска. В этом случае x_i(t)=x_i(t)+N(0,C) , где N(0,C) обозначает нормальное распределение вектора 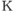с нулевым математическим ожиданием и плотностью вероятностей $f_G(r)=\frac{det\ C}{(2\pi)_x^n}e^{-\frac{1}{2}r^rCr}$ .

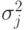Здесь диагональные элементы $C^{-1}$ - вариации $\sigma_j^2$ , а не- диагональные элементы – ковариации величин шагов мутации. При этом ковариации определяются углами вращения, которые необходимо произвести, чтобы преобразовать некоррелированный вектор мутации в коррелированный вектор. Если $\omega_i(t)$ означает угол вращения вектора для -ой особи, то особь представляется триплетом $x_i(t)=(x_i(t),\sigma_i(t),\omega_i(t))$ , где

$x_i(t)\in R^{n_x},\sigma_i(t)\in R_+^{n_x},\omega_i(t)\in R^{n_x(n_x-1)/2},\mbox{и}\\\omega_{ik}(t)\in(0,2\pi],k=1,\dots,n_x(n_x-1/2)$

( 9.9)

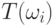Углы вращения используются при представлении ковариаций для n_x генетических переменных генетического вектора x_i . Поскольку ковариационная матрица симметрична, можно использовать вектор для представления углов вместо матрицы. Углы вращения можно использовать для вычисления ортогональной матрицы вращения $T(\omega_i)$ следующим образом:

$T(\omega_i)=\prod_{i=1}^{n_x-1}\prod_{j=i+1}^{n_x}R_{ij}(\omega_i),$

( 9.10)

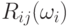которая является произведением n_x(n_x-1)/2 матриц вращения. Каждая матрица вращения $R_{ij}(\omega_i)$ является единичной матрицей с $r_u=\cos(\omega_{ik})$ и $r_{lj}=-r_{jl}=-\sin(\omega_{ik})$ , с $k=1\Leftrightarrow(l=1,j=2),k=2\Leftrightarrow(l=1,j=3),\dots$ .

Построенная матрица вращения используется в операторе мутации.

Итак, в ЭС используются два вида параметров: 1) стандартные отклонения величины шага мутации; 2) углы вращения, которые представляются ковариациями размера шага мутации. Пусть $n_{\sigma}$ обозначает число используемых параметров отклонений и $n_{\omega}$ - число углов вращения. На практике имеют место, в основном, следующие типовые ситуации:

$n_{\sigma}=1,n_{\omega}=0$ , т.е. используется только один параметр отклонения $((\sigma_j=\sigma\in R_+,j=1,j=2),k=2\Leftrightarrow(l=1,j=3),\dots.)$ , одинаковый для всех компонент генотипа нулевые углы вращения. При этом распределение вероятностей имеет круглую форму, что показано на рис.9.1а. Середина окружности определяет позицию родительской особи , в то время как $\sigma$ указывает на отклонение величины шага.
Отметим, что это распределение фактически показывает вероятность позиции потомка 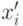, имеющей наиболее высокую вероятность в центре. Тогда параметр регулируется следующим образом - $\sigma_i^t=\sigma_i(t)e^{\tau N(0,1)}$ , где $\tau=\frac{1}{\sqrt{n_z}}$ . При этом регулирование одного параметра выполняется быстро, но подход является не гибким в том случае, когда координаты имеют различные градиенты.

Рис. 9.1. Иллюстрация распределений вероятностей мутации.
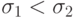$n_{\sigma}=n_x,n_{\omega}=0$ , где каждая компонента имеет свой собственный параметр отклонения. В этом случае распределение мутации имеет эллиптическую форму, как показано на рис.9.1b, где $\sigma_1<\sigma_2$ . Тогда увеличение числа параметров вызывает линейное увеличение вычислительной сложности, но дополнительные степени свободы обеспечивают большую гибкость. При этом могут учитываться различные значения градиентов по разным осям. Значения параметров корректируются в соответствии со следующими формулами:
$\sigma_1{ij}(t)=\sigma_{ij}(t)e^{\tau'N(0,1)+\tau N_j(0,1)},\mbox{где }\tau^t=\frac{1}{\sqrt{2n_x}}\ and\ \tau=\frac{1}{\sqrt{2\sqrt{n_x}}}$ ( 9.11)
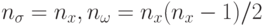$n_{\sigma}=n_x,n_{\omega}=n_x(n_x-1)/2$ , где в качестве параметров кроме отклонений (девиаций) используются также углы вращения. В этом случае эллиптическое распределение мутации вращается относительно осей координат как показано на рис.9.1с. Эти вращения позволяют найти лучшую аппроксимацию контуров в пространстве поиска. Тогда параметры отклонений корректируются в соответствии с предыдущей формулой (9.11), а значения углов по нижеприведенной формуле $\omega_{ik}^t(t)=\omega_{ik}(t)+\gamma N_j(0,1)\mod 2\pi,\mbox{где }\gamma\approx 0.0873$ . Расширение параметров путем ввода углов вращения повышает гибкость, но вычислительная сложность при этом растет квадратично.
$1<n_{\sigma}<n_x$ , где допускается еще больше степеней свободы. Для всех $j>n_{\sigma}$ используется отклонение $\sigma_{n_{\sigma}}$ .

Стратегии самоадаптации. Чаще всего при самоадаптации параметров ЭС применяется механизм, основанный на логарифмически нормальном распределении, который описан в следующем разделе 9.4. Кроме этого могут быть применены аддитивные методы, также представленные в разделе 9.4.

В работе [5] предложен метод адаптации параметров на основе "обучения с подкреплением", в котором параметры корректируются следующим образом:

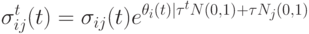$\sigma_{ij}^t(t)=\sigma_{ij}(t)e^{\theta_i(t)|\tau^tN(0,1)+\tau N_j(0,1)}$

( 9.12)

где $\theta_i(t)$ - сумма временных поощрений за последние $n_{\theta}$ поколений для -ой особи, то есть

$\theta_i(t)=\frac{1}{n_{\theta}}\sum_{t'=0}^{n_{\theta}}\theta_i(t-t').$

( 9.13)

Для вычисления поощрений можно использовать различные методы для каждой особи на каждом временном шаге. Например, в работе [5] предложено это делать следующим образом

$\theta_i(t)=\left\{\begin{array}\ 0.5\mbox{ если }\Delta f(x_i(t))>0\\0\mbox{ если }\Delta f(x_i(t))=0\\-1\mbox{ если }\Delta f(x_i(t))<0\end{array}\right\},$

( 9.14)

где ухудшение значений фитнесс-функции сурово штрафуется. Здесь 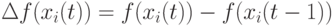$\Delta f(x_i(t))=f(x_i(t))-f(x_i(t-1))$ .

В работе [6] использовались поощрения +1, 0 или -1 в зависимости от полученных характеристик. Кроме этого, в этой же работе предложено применять:

$\theta_{ij}(t)=f(x_i(t))-f(x_i(t-\Delta t)),\mbox{с }0<\Delta t<t$ ( 9.15)
Этот подход определения поощрения основан на учете изменений на уровне фенотипа, поскольку определяется фитнесс-функцией. При этом чем больше особь улучшает значение фитнесс-функции, тем она получает большее поощрение. С другой стороны, худшее значение фитнесс-функции особи ведет к увеличению штрафа для этой особи
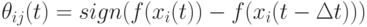$\theta_{ij}(t)=sign(f(x_i(t))-f(x_i(t-\Delta t)))$ . Эта схема дает значения поощрений +1, 0 или -1.
$\theta_{ij}(t)=\|x_i(t)-x_i(t-\Delta t)\|sign(f(x_i(t))-f(x_i(t-\Delta t)))$ .

Здесь поощрение пропорционально размеру шага в пространстве решений.

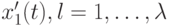
В [7] рассматривается схема самоадаптации, где $n_{\sigma}=1$ и применяется ковариационная матрица. В этой схеме отклонение потомка определяется как функция отклонений производящих его родителей. Здесь для каждого потомка $x'_1(t),l=1,\dots,\lambda$

$\sigma'_l(t)=\sqrt[p]{\prod_{i\in\Omega_i(t)}\sigma_i(t)e^{\xi}},$

( 9.16)

где $\Omega_i(t)$ - индекс множества $\rho$ родителей потомка x'_1(t) и распределение $\xi$ такое, что $prob(\xi=0.4)=prob(\xi=-0.4)=0.5$ . В разделе 9.4 (оператор мутации) показано, как эта схема самоадаптации может быть использована в операторе мутации.

В работе [8] применяется схема самоадаптации, где $1<n_{\sigma}<n_x$ и каждая особь использует различное количество параметров отклонений $n_{\sigma i}(t)$ . На каждой итерации число параметров отклонений может быть увеличено или уменьшено с вероятностью 0.05. Если число параметров отклонений увеличивается, то новый параметр отклонения инициализируется следующим образом: