| Россия, г. Казань |
Оптимизации для параллельных вычислений
Презентацию к лекции Вы можете скачать здесь.
Тенденция в развитии микропроцессоров:
Оптимизирующий компилятор – инструмент, транслирующий исходный код программы в исполняемый модуль, а так же инструмент, оптимизирующий исходный код для получения лучшей производительности. Распараллеливание – трансформация последовательно исполняемой программы в программу, в которой наборы инструкций выполняются одновременно и сохраняется результат работы.
Изначально компьютеры имели одно логическое устройство, исполняющее инструкции последовательно. Программы разрабатывались для последовательного выполнения инструкций и большинство программных языков работали в соответствии с этим принципом. Однако в последствии при развитии архитектуры процессоров много усилий было приложено к тому, чтобы достичь одновременного выполнения нескольких инструкций. Параллелизм в данном случае трактуется как одновременное выполнение нескольких операций.
(Если говорить о развитии параллелизма в процессоре, то можно упомянуть такие технологии как конвейеризация pipelining, суперскалярность, многоядерность и многопроцессорность). Развитие процессорных технологий поставило вопрос о трансформации последовательно выполняющейся программы в программу, где полностью используются возможности вычислительной системы и инструкции выполняются одновременно в той мере насколько это поддерживается вычислительной системой и необходимостью сохранить "смысл" выполняемой программы.
Трансформациями программы из программного языка в инструкции микропроцессора занимается компилятор. Современные компиляторы - это мощные средства разработки, включающие в себя разнообразные интерфейсные и отладочные средства, производящие выполняемые модули для различных архитектур и использующие массу оптимизаций для улучшения производительности программы.
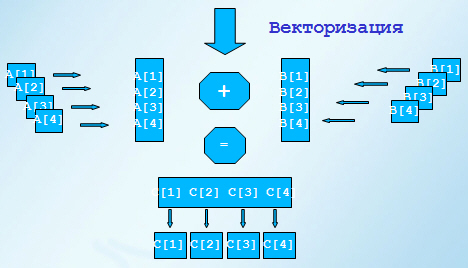
Одна из технологий распараллеливания программы – векторизация циклов
C[1] = A[1]+B[1]
C[2] = A[2]+B[2]
C[3] = A[3]+B[3]
C[4] = A[4]+B[4]
Поскольку большую часть времени работы программа проводит внутри различных циклов и синтаксис тела цикла обычно хорошо определен, то векторизация циклов - это одна из самых мощных компиляторных оптимизаций. Идея векторизации базируется на использовании векторов данных и наличии векторных операций, работающих с векторными операндами. Таким образом формально вместо последовательного выполнения группы скалярных операций получаем одновременное выполнение этих операций.
Типичная векторная инструкция представляет собой операцию над двумя векторами в памяти или в регистрах фиксированной длины. Векторные регистры могут быть загружены из памяти за одну операцию или по частям.
Векторизация - это компиляторная оптимизация, которая заменяет скалярный код на векторный. Эта оптимизация "упаковывает" данные в вектора и заменяет скалярные операции на операции с такими векторами (пакетами).
A(1:n:k) – секция массива в Фортране.
for(i=0;i<U,i++) { for(i=0;i<U;i+=vl) {
S1: lhs1[i] = rhs1[i]; S1: lhs1[i:i+vl-1:1] = rhs1[i:i+vl-1:1];
… => …
Sn: lhsn[i] = rhsn[i]; Sn: lhsn[i:i+vl-1:1] = rhsn[i:i+vl+1:1];
} }
В Фортране есть очень подходящая языковая структура для описания оптимизации векторизация, а именно "секция массива". Т.е. Секция массива это область памяти, содержащая несколько последовательных элементов, возможно разделенных постоянным отступом. Формально мы можем в векторный регистр заполнить любыми переменными, но в случае векторизации работа идет в основном именно с элементами массива.
MMX,SSE Векторные инструкции и векторизация
Первоначально была предложена технология MMX.
MMX (Multimedia Extensions) – набор инструкций, выполняющих характерные для процессов кодирования/декодирования потоковых аудио/видео данных действия.
MMM0-MMM7 64 битные регистры для работы с целыми числами концепция пакетов, каждый из этих регистров мог хранить
47 инструкций, которые делятся на несколько груп:
Эта технология ведет свое начало от инструкций сопроцессора для обработки вещественных чисел или чисел с плавающей точкой. Устройство обработки чисел с плавающей точкой (FPU) было интегрировано в 80486 DX МП. Эта интеграция добавила в МП новые регистры, а именно 8 80-битных регистров данных для хранения чисел с плавающей точкой. Интеграция существенно улучшила скорость работы с вещественными числами. Но при работе с целыми числами эта часть компилятора простаивала.
Для того, чтобы позволить использовать FPU в Pentium MMX МП была предложена новая технология MMX. Ее идея заключалась в том, что в МП добавлялись новые регистры (8 64 битных MM0-MM7), которые адресовались (алиасились) к FPU регистрам и набор инструкций микропроцессора дополнялся рядом инструкций (SIMD Single Instruction, Multiple Data), работающих с этими регистрами и выполнявшими над ними целочисленные операции. Вводилась концепция пакетов, т.е. каждый из этих регистров мог хранить
Недостатком была невозможность одновременно работать с целыми и вещественными числами, MMX инструкции были предназначены для работы с целыми.
SSE (Streaming SIMD Extensions, потоковое SIMD-расширение процессора)
Это набор инструкций, позволяющий работать с множеством данных – SIMD(Single Instruction, Multiple Data, Одна инструкция — множество данных).
- поддерживает 8 128-битных регистров (xmm0 до xmm7)
- производит операции со скалярными и упакованными типами данных набор инструкций.
Технология EMM64T добавляла к этому набору еще 8 128 битных регистра (xmm8 до xmm15).
SSE2,SSE3,SSEE3,SSE4 – последующие расширения этой идеи.
SSE2 добавил тип упакованных данных с плавающей точкой двойной точности.
AVX новое расширение системы команд (Advanced vector extensions)
AVX предоставляет различные улучшения, новые инструкции и новую схему кодирования машинных кодов.
Размер векторных регистров SIMD увеличивается с 128 до 256 бит.
Регистры YMM0-YMM15
Существующие 128-битные инструкции используют младшую половину YMM регистров.
Технология SSE была впервые реализована в Pentium3.
Появление этого набора инструкций позволило решить проблему одновременной работы с упакованными целыми и вещественными данными. Теперь упакованные целые обрабатываются с помощью MMX, в то же время вещественные вычисления проводятся с помощью SSE и векторных регистров.
Помимо векторных регистров SSE добавил в вычислительную систему 32-битный регистр флагов и операции с этим регистром
Расширился набор SIMD операций над целыми
Были добавлены инструкции явной предвыборки данных, контроля кэширования данных и контроля порядка операций сохранения
Расширения инструкций CPUID для получения информации о процессоре.
SSE2 – расширяет набор инструкций SSE с целью полного вытеснения MMX
Преимущество в производительности достигается в том случае, когда необходимо произвести одну и ту же последовательность действий над разными данными.
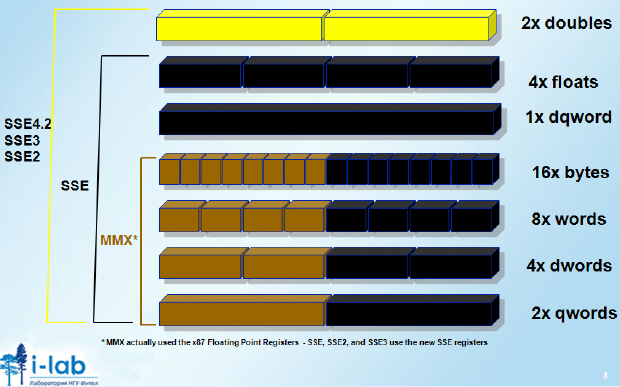
Данные различных типов могут быть упакованы в векторные регистры следующим образом:
Выбор подходящего для вычислений типа данных может существенно сказаться на производительности приложения.
При обсуждении возможного выигрыша от векторизации нужно учитывать тот простой факт, что в векторные регистры может быть упаковано различное количество элементов одного типа. Формально, можно предположить, что векторизация тем более выгодна, чем больше скалярных элементов используемого типа может быть размещено в векторном регистре.
Use –QxW for P4 SIMD data types
64 bit double + 64 bit double = 128 bit register
32 bit + 32 bit + 32 bit + 32 bit (floats) = 128 bit register
Три набора опций для использования процессорно- специфических расширений
- Опции –Qx<EXT> например –QxSSE4_1
- Проводит проверку процессора
- Ошибка времени выполнения в случае запуска программы на процессоре отличном от указанного в опции
- Опции –arch:<EXT> например –arch:SSE3
- Нет проверки
- Падение программы при выполнении специфической процессорной инструкции в случае запуска на процессоре не поддерживающем указанное расширение
- Опции –Qax<EXT> например –QaxSSE4_2
- Автоматический выбор оптимального варианта – наличие кода для разных векторных расширений
- Проверка процессора доступна только для Интеловских процессоров
- Для не Интеловского процессора используется умолчательный код
- Умолчательная опция –mSSE2
Допустимость векторизации
Векторизация – перестановочная оптимизация. Операции меняют порядок выполнения.
Перестановочные оптимизации допустимы, если не изменяется порядок зависимостей.
Таким образом мы получили критерий допустимости векторизации в терминах зависимостей.
Простейший вариант – зависимостей в векторизуемом цикле нет.
Зависимости в векторизуемом цикле есть, но их порядок после векторизации совпадает с порядком в невекторизованном цикле.
Определить существуют или нет зависимости для данного цикла – непростая задача. Компилятор использует оценочные технологии для решения этой проблемы. Дополнительные сложности возникают с указателями в C. Поскольку указатели могут указывать на пересекающиеся области памяти одной из важных задач является доказательство того, что указатели указывают на различные участки памяти.
Упрощает ситуацию для анализа допустимости векторизации тот факт, что векторизация выполняется как правило для внутреннего цикла.
/Qvec-report[n]
control amount of vectorizer diagnostic information
n=0 no diagnostic information
n=1 indicate vectorized loops (DEFAULT)
n=2 indicate vectorized/non-vectorized loops
n=3 indicate vectorized/non-vectorized loops and prohibiting
data dependence information
n=4 indicate non-vectorized loops
n=5 indicate non-vectorized loops and prohibiting data
dependence information
Использование: icl -c -Qvec-report3 loop.c
Примеры диагностики:
C:\loops\loop1.c(5) (col. 1): remark: LOOP WAS VECTORIZED.
C:\loops\loop3.c(5) (col. 1): remark: loop was not vectorized: vectorization possible but seems inefficient.
C:\loops\loop6.c(5) (col. 1): remark: loop was not vectorized: nonstandard loop is not a vectorization candidate.
В случае векторизации есть опция –Qvec-report, которая позволяет получить компиляторную диагностику и понять был ли распознан цикл;
Фортран активно используется в описании векторизации, поскольку имеет удобное понятие секции массива.
В упрощенном виде:
DO I=1,N
A(I)=…
END DO
при векторизации переводится в
DO I=1,N/K
A(I:I+K)=…
END DO
где K – число элементов матрицы A размещаемых в векторном регистре.
Наглядным критерием возможности векторизации является то факт, что введение секций массива не порождает зависимостей.
DO I=1,N DO I=1,N/K
A(I)=A(I)+C => A(I:I+K) = A(I:I+K)+C
END DO END DO
Может быть векторизован.
DO I=1,N DO I=1,N/K
A(I+1)=A(I)+C => A(I+1:I+1+K)=A(I:I+K)+C
END DO END DO
Не может быть векторизован.
По определению зависимость существует если
- есть два утверждения, которые обращаются к одной и той-же памяти и по крайней мере одно из них пишет в память
- существует возможный путь от одного утверждения к другому. В предложенных примерах в первом случае в цикле нет утверждений, которые бы обращались к одной и той же памяти, а в плохом случае секции "накладываются" друг на друга, поэтому если взять I и I+1 итерацию, то будем иметь I(I+1:I+1+K) из левой части утверждения (пишем в память) и I(I+K:I+2K) из правой части. Т.е. утверждения на итерациях I и I+1 работают с одной и той-же памятью, возможный путь существует – есть зависимость.
PROGRAM TEST_VEC
INTEGER,PARAMETER :: N=1000
#ifdef PERF
INTEGER,PARAMETER :: P=4
#else
INTEGER,PARAMETER :: P=3
#endif
INTEGER A(N)
DO I=1,N-P
A(I+P)=A(I)
END DO
PRINT *,A(50)
END
|
Предположение:
Цикл можно векторизовать, если дистанция для зависимости >= K, где K – количество элементов массива, входящих в векторный регистр. Проверяем утверждение с помощью компилятора:
ifort test.F90 -o a.out –vec_report3
echo -------------------------------------
ifort test.F90 -DPERF -o b.out –vec_report3
./build.sh
test.F90(11): (col. 1) remark: loop was not vectorized: existence of vector dependence.
-------------------------------------
test.F90(11): (col. 1) remark: LOOP WAS VECTORIZED.
|
Опции группы vec_report (Qvec_report) информируют пользователя о действиях векторизатора.