| Россия, г. Москва |
Лекция 2: Принципы переноса прикладных программных пакетов на Intel Xeon Phi
Программная реализация
Рассмотрим базовую программную реализацию метода FDTD. Сеточные значения электрического и магнитного поля будем хранить как динамические 3-мерные массивы из 3-компонентных векторов. Ядро реализации составляют функции обновления сеточных значений  и
и  , являющиеся прямой записью разностной схемы метода FDTD. Приведем код данных функций:
, являющиеся прямой записью разностной схемы метода FDTD. Приведем код данных функций:
struct Double3 {
double x, y, z;
};
struct Parameters {
int nx, ny, nz;
double dx, dy, dz, dt;
};
const double C = 29979245800.0;
void updateE(const Parameters & parameters, Double3 *** b, Double3 *** e)
{
const double cx = C * parameters.dt / parameters.dx;
const double cy = C * parameters.dt / parameters.dy;
const double cz = C * parameters.dt / parameters.dz;
#pragma omp parallel for
for (int i = 0; i < parameters.nx; i++)
for (int j = 0; j < parameters.ny; j++)
for (int k = 0; k < parameters.nz; k++)
{
e[i][j][k].x += cy * (b[i][j + 1][k].z - b[i][j][k].z) - cz * (b[i][j][k + 1].y - b[i][j][k].y);
e[i][j][k].y += cz * (b[i][j][k + 1].x - b[i][j][k].x) - cx * (b[i + 1][j][k].z - b[i][j][k].z);
e[i][j][k].z += cx * (b[i + 1][j][k].y - b[i][j][k].y) - cy * (b[i][j + 1][k].x - b[i][j][k].x);
}
}
void updateB(const Parameters & parameters, Double3 *** e, Double3 *** b)
{
const double cx = C * parameters.dt / parameters.dx;
const double cy = C * parameters.dt / parameters.dy;
const double cz = C * parameters.dt / parameters.dz;
#pragma omp parallel for
for (int i = 1; i <= parameters.nx; i++)
for (int j = 1; j <= parameters.ny; j++)
for (int k = 1; k <= parameters.nz; k++)
{
b[i][j][k].x += cz * (e[i][j][k].y - e[i][j][k - 1].y) - cy * (e[i][j][k].z - e[i][j - 1][k].z);
b[i][j][k].y += cx * (e[i][j][k].z - e[i - 1][j][k].z) - cz * (e[i][j][k].x - e[i][j][k - 1].x);
b[i][j][k].z += cy * (e[i][j][k].x - e[i][j - 1][k].x) - cx * (e[i][j][k].y - e[i - 1][j][k].y);
}
}
В функциях updateE, updateB из циклов вынесены инварианты 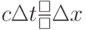 ,
,  ,
,  . Произведено прямолинейное распараллеливание циклов с независимыми итерациями с помощью OpenMP. Данные функции выполняют обновление сеточных значений области во "внутренней области" – без учета граничных условий. Учет граничных условий делается в отдельных функциях для исключения условных операций в основных циклах и упрощения использования других типов граничных условий. Таким образом, основной вычислительный цикл имеет вид:
. Произведено прямолинейное распараллеливание циклов с независимыми итерациями с помощью OpenMP. Данные функции выполняют обновление сеточных значений области во "внутренней области" – без учета граничных условий. Учет граничных условий делается в отдельных функциях для исключения условных операций в основных циклах и упрощения использования других типов граничных условий. Таким образом, основной вычислительный цикл имеет вид:
for (int t = 0; t < numSteps; t++)
{
updateE(parameters, b, e);
updateBoundaryE(parameters, e);
updateB(parameters, b, e);
updateBoundaryB(parameters, b);
}
В силу сходства функций updateE, updateB в дальнейшем будем демонстрировать техники оптимизации лишь для updateE, подразумевая выполнение аналогичных преобразований и для updateB. Для анализа производительности будем использовать следующий бенчмарк: моделирование распространения плоской волны на сетке 256x256x256 со 100 итерациями по времени.
Эксперименты проводились на следующей инфраструктуре:
| Процессор | 2x Intel Xeon Xeon E5-2690 (2.9 GHz, 8 ядер) |
| Сопроцессор | Intel Xeon Phi 7110X |
| Память | 64 GB |
| Операционная система | Linux CentOS 6.2 |
| Компилятор, профилировщик, отладчик | Intel C/C++ Compiler 13 |
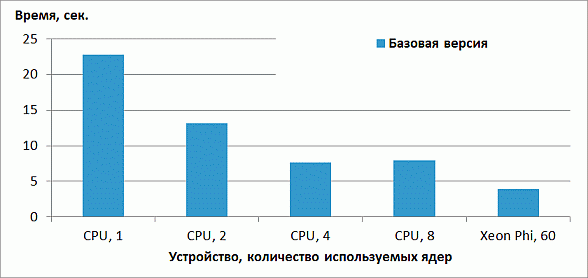
Результаты производительности базовой версии на CPU и Xeon Phi в режиме только сопроцессора приведены на рис. 1. CPU-версия неидеально масштабируется с 1 до 4 ядер и демонстрирует замедление при переходе от 4 до 8 ядер. Версия на Xeon Phi немного обгоняет CPU-версию. Во всех запусках на Xeon Phi используется 1 поток на ядро. Данный выбор нетипичен для большинства приложений рекомендуется использование от 2 до 4 потоков на ядро. Однако для рассматриваемого приложения опытным путем было определено, что оптимальной конфигурацией запуска является 1 поток на ядро. Возможное обоснование состоит в том, что производительность ограничена в первую очередь пропусккой способностью памяти, а не скоростью выполнения вычислительных операций.
Оптимизация 1: векторизация и изменение структуры данных
Для исследования возможности векторизации кода воспользуемся отчетом о векторизации с помощью опции компилятора –vec-report3. Как видно из отчета, основные циклы (внутренние циклы в updateE, updateB) не векторизуются из-за неподдерживаемой структуры цикла:
naive.cpp(24): (col. 5) remark: loop was not vectorized: unsupported loop structure
Причина в том, что в условии цикла используется поле структуры Parameters. Для преодоления данной проблемы скопируем parameters.nz в локальную переменную и будем использовать ее в условии цикла.
После этого структура цикла становится пригодной для векторизации, однако векторизация не происходит из-за потенциальных зависимостей между итерациями (список потенциальных зависимостей зависимостей очень длинный, приведено его начало):
naive.cpp(25): (col. 5) remark: loop was not vectorized: existence of vector dependence naive.cpp(27): (col. 9) remark: vector dependence: assumed ANTI dependence between b line 27 and e line 29 naive.cpp(29): (col. 9) remark: vector dependence: assumed FLOW dependence between e line 29 and b line 27 naive.cpp(27): (col. 9) remark: vector dependence: assumed ANTI dependence between b line 27 and e line 31 naive.cpp(31): (col. 9) remark: vector dependence: assumed FLOW dependence between e line 31 and b line 27 naive.cpp(27): (col. 9) remark: vector dependence: assumed ANTI dependence between b line 27 and e line 27
Действительно, в случае перекрытия массивов в памяти векторизация цикла может быть некорректной, поэтому компилятор не вправе ее осуществить.
Разработчик кода обладает информацией о том, что массивы не пересекаются в памяти и может повлиять на векторизацию цикла с использованием нескольких средств: #pragma ivdep , #pragma simd , ключевое слово restrict , ключ -ansi-alias . Воспользуемся #pragma simd для векторизации внутреннего цикла и соберем программу с ключом -ansi-alias . Кроме того, для повышения производительности сделаем выделение памяти выровненным по 64, используя при выделении массивов сеточных значений функцию _mm_malloc . Функция updateE принимает вид:
void updateE(const Parameters & parameters, Double3 *** b, Double3 *** e)
{
const double cx = C * parameters.dt / parameters.dx;
const double cy = C * parameters.dt / parameters.dy;
const double cz = C * parameters.dt / parameters.dz;
const int nz = parameters.nz;
#pragma omp parallel for
for (int i = 0; i < parameters.nx; i++)
for (int j = 0; j < parameters.ny; j++)
#pragma simd
for (int k = 0; k < nz; k++)
{
e[i][j][k].x += cy * (b[i][j + 1][k].z - b[i][j][k].z) - cz * (b[i][j][k + 1].y - b[i][j][k].y);
e[i][j][k].y += cz * (b[i][j][k + 1].x - b[i][j][k].x) - cx * (b[i + 1][j][k].z - b[i][j][k].z);
e[i][j][k].z += cx * (b[i + 1][j][k].y - b[i][j][k].y) - cy * (b[i][j + 1][k].x - b[i][j][k].x);
}
}
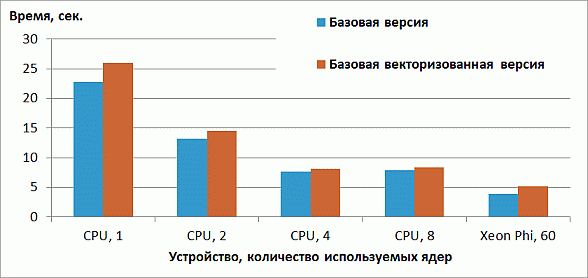
Результаты производительности данной версии приведены на рис. 2.2.
Как видно из рис. 2.2, векторизация не только привела к повышению производительности, но даже немного замедлила код. Наиболее вероятная причина данного эффекта состоит в том, что загрузка данных из памяти производится неэффективно и векторизация лишь усиливает расходы на загрузку данных.
Для повышения эффективности загрузки данных из памяти воспользуемся стандартной техникой преобразования массива структур в структуру массивов. Для каждого из полей вместо хранения массива Double3 будем использовать отдельный массив из double для каждой компоненты. Кроме того, перепишем внутренний цикл в терминах работы с одномерными массивами. Код приобретает следующий вид:
void updateE(const Parameters & parameters, double *** bx, double *** by, double *** bz,
double *** ex, double *** ey, double *** ez)
{
const double cx = C * parameters.dt / parameters.dx;
const double cy = C * parameters.dt / parameters.dy;
const double cz = C * parameters.dt / parameters.dz;
const int nz = parameters.nz;
#pragma omp parallel for
for (int i = 0; i < parameters.nx; i++)
for (int j = 0; j < parameters.ny; j++)
{
double * ex_ij = ex[i][j];
double * ey_ij = ey[i][j];
double * ez_ij = ez[i][j];
const double * bx_ij = bx[i][j];
const double * bx_ij1 = bx[i][j + 1];
const double * by_ij = by[i][j];
const double * by_i1j = by[i + 1][j];
const double * bz_ij = bz[i][j];
const double * bz_i1j = bz[i + 1][j];
const double * bz_ij1 = bz[i][j + 1];
#pragma simd
for (int k = 0; k < nz; k++)
{
ex_ij[k] += cy * (bz_ij1[k] - bz_ij[k]) -
cz * (by_ij[k + 1] - by_ij[k]);
ey_ij[k] += cz * (bx_ij[k + 1] - bx_ij[k]) -
cx * (bz_i1j[k] - bz_ij[k]);
ez_ij[k] += cx * (by_i1j[k] - by_ij[k]) -
cy * (bx_ij1[k] - bx_ij[k]);
}
}
}
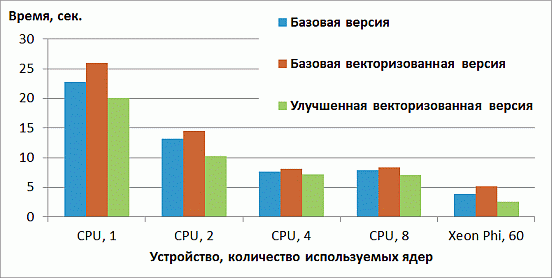
Результаты версии с учетом данных изменений приведены на рис. 2.3. Векторизация дает почти двукратное ускорение на Xeon Phi и небольшое ускорение на CPU. Данные ускорения весьма далеки от теоретически максимально возможных: на Xeon Phi векторные операции могут осуществляться с 8 значениями типа double, а на используемом CPU – с 4. Это объясняется тем, что задача в первую очередь ограничена доступом к памяти. С другой стороны, именно большая пропускная способность памяти главным образом обеспечивает превосходство Xeon Phi над CPU.