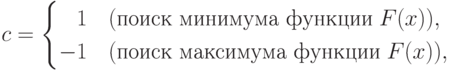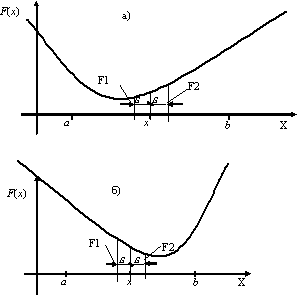Лекция 9: Однопараметрическая (одномерная) оптимизация. Методы одномерной оптимизации: метод дихотомии, метод Фибоначчи, метод "золотого сечения", метод Ньютона.

Однопараметрическая оптимизация (поиск экстремумов функций одной переменной) является самостоятельной и часто встречаемой задачей. Кроме того, к ней сводится гораздо более сложная задача - поиск экстремума функции многих переменных.

1. Метод дихотомии.

Рассмотрим простейший однопараметрический метод безусловной оптимизации – метод дихотомии. Этот метод является методом прямого поиска. В нем при поиске экстремума целевой функции используются только вычисленные значения целевой функции.

Дана функция F(x). Необходимо найти , доставляющий минимум (или максимум) функции F(x) на интервале [a,b] с заданной точностью , т.е. найти

Запишем словесный алгоритм метода.

1) На каждом шаге процесса поиска делим отрезок [a,b] пополам, x=(a+b)/2 - координата середины отрезка [a,b].

2) Вычисляем значение функции F(x) в окрестности 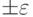вычисленной точки x, т.е.

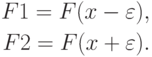
3) Сравниваем F1 и F2 и отбрасываем одну из половинок отрезка [a,b] (рис. 9.1).

При поиске минимума:

Если F1<F2, то отбрасываем отрезок [x,b], тогда b=x. (рис. 9.1.а)

Иначе отбрасываем отрезок [a,x], тогда a=x. (рис. 9.1.б)

При поиске максимума:

Если F1<F2, то отбрасываем отрезок [a,x], тогда a=x.

Иначе отбрасываем отрезок [x,b], тогда b=x.

4) Деление отрезка [a,b] продолжается, пока его длина не станет меньше заданной точности , т.е.

Рис. 9.1. Поиск экстремума функции F(x) методом дихотомии

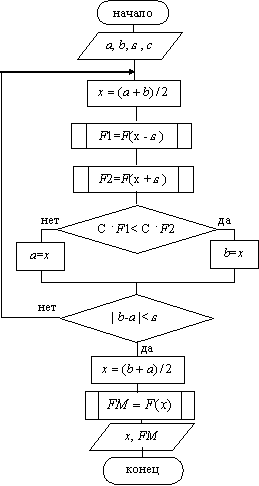
Схема алгоритма метода дихотомии представлена на рис 9.2.

На рис 9.2: c - константа,

Рис. 9.2. Схема алгоритма метода дихотомии