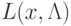| Россия |
Лекция 7: Нелинейное программирование. Классификация методов нелинейного программирования. Классический метод определения условного экстремума. Метод множителей Лагранжа
4. Метод множителей Лагранжа
Метод множителей
Лагранжа позволяет отыскивать максимум  или минимум
или минимум  функции при ограничениях-равенствах. Основная идея метода
состоит в переходе от задачи на условный экстремум к задаче
отыскания безусловного экстремума некоторой построенной
функции Лагранжа. Пусть задана задача НП при
ограничениях-равенствах вида
функции при ограничениях-равенствах. Основная идея метода
состоит в переходе от задачи на условный экстремум к задаче
отыскания безусловного экстремума некоторой построенной
функции Лагранжа. Пусть задана задача НП при
ограничениях-равенствах вида
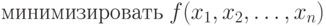 |
( 4.1) |
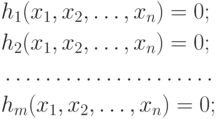 |
( 4.2) |
Предположим, что все функции f, h1, h2, ..., hm
- дифференцируемы. Введем набор переменных 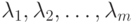 (число которых равняется числу ограничений), которые называются множителями Лагранжа,
и составим функцию Лагранжа такого вида:
(число которых равняется числу ограничений), которые называются множителями Лагранжа,
и составим функцию Лагранжа такого вида:
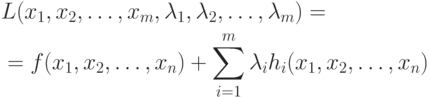 |
( 4.3) |
Справедливо такое утверждение: для того чтобы вектор 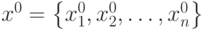 являлся решением задачи (4.1) при ограничениях (4.2), необходимо,
чтобы существовал такой вектор
являлся решением задачи (4.1) при ограничениях (4.2), необходимо,
чтобы существовал такой вектор 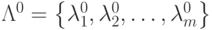 ,
что пара векторов удовлетворяла бы системе уравнений
,
что пара векторов удовлетворяла бы системе уравнений
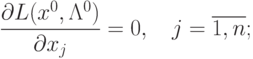 |
( 4.4) |
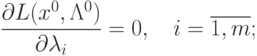 |
( 4.5) |
Покажем необходимость условий (4.4), (4.5) на простом примере:
 |
( 4.6) |
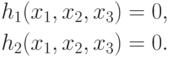 |
( 4.7) |
Ограничения (4.7) определяют допустимую область S, которая представляет собой кривую в пространстве R(2) и является результатом пересечения h1(x) и h2(x).
Допустим, что рассматриваемая задача имеет точку минимума в S1: 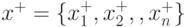 ,
функции f, h1, h2 имеют непрерывные
производные первого порядка на некотором открытом множестве и градиенты
,
функции f, h1, h2 имеют непрерывные
производные первого порядка на некотором открытом множестве и градиенты
![\nabla h_1(x) = \left[ \frac{\partial h_1}{\partial x_1} ;
\frac{\partial h_1}{\partial x_2} ;
\frac{\partial h_1}{\partial x_3} ;
\right]^T ; \quad
\nabla h_1(x) = \left[ \frac{\partial h_2}{\partial x_1} ;
\frac{\partial h_2}{\partial x_2} ;
\frac{\partial h_2}{\partial x_3} ;
\right]^T](/sites/default/files/tex_cache/2c8e0c787f886bc78626672ac22337ae.png)
Если две переменные в уравнениях (4.7) можно выразить через третью в виде x2=U(x1), x3=V(x1), то подставив их в целевую функцию (4.6), преобразуем исходную задачу в следующую задачу без ограничений, которая содержит лишь одну переменную x1:
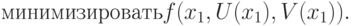 |
( 4.8) |
Поскольку градиенты 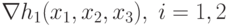 ,
непрерывны и линейно независимы, то можно применить известную теорему
математического анализа о неявной функции и найти стационарную точку
,
непрерывны и линейно независимы, то можно применить известную теорему
математического анализа о неявной функции и найти стационарную точку 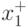 , а потом
, а потом 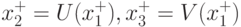 .
.
Приведенный подход можно в принципе распространить и на случай функции n переменных ![f(x), x=[x_1, x_2, \ldots, x_n]^T](/sites/default/files/tex_cache/8d10e4802673bd098b3c083af6adf798.png) при наличии m ограничений-равенств:
при наличии m ограничений-равенств:
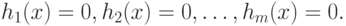 |
( 4.9) |
Если функции 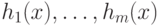 удовлетворяют условиям теоремы о неявной функции,
то m из n переменных уравнений (4.9)
можно выразить через остальные (n-m) переменных,
подставить их в f(x) и таким образом преобразовать
задачу минимизаци с ограничениями в задачу безусловной минимизации
с (n-m) переменными. Однако такой подход трудно
реализовать на практике, поскольку очень трудно разрешить
уравнения (4.9) относительно некоторых переменных.
В общем случае это совсем невозможно.
удовлетворяют условиям теоремы о неявной функции,
то m из n переменных уравнений (4.9)
можно выразить через остальные (n-m) переменных,
подставить их в f(x) и таким образом преобразовать
задачу минимизаци с ограничениями в задачу безусловной минимизации
с (n-m) переменными. Однако такой подход трудно
реализовать на практике, поскольку очень трудно разрешить
уравнения (4.9) относительно некоторых переменных.
В общем случае это совсем невозможно.
Поэтому рассмотрим другой подход, который базируется на методе множителей Лагранжа.
Пусть x+ - точка минимума f(x), определяемого выражением (4.8). В соответствии с известной теоремой математического анализа о неявной функции можно записать
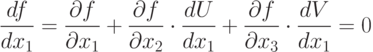 |
( 4.10) |
Аналогичные соотношения получим для ограничений
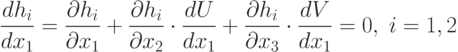 |
( 4.11) |
Запишем уравнения (4.10), (4.11) совместно в виде
![A \times \left[
\begin{aligned}
& 1 \\
& \frac{dU}{dx_1} \\
& \frac{dV}{dx_1}
\end{aligned}
\right] =0,](/sites/default/files/tex_cache/92a9277af4979c21d2126bbb2f6187db.png) |
( 4.12) |
![A = \left[
\begin{aligned}
& \nabla f (x^+) \\
& \nabla h_1 (x^+) \\
& \nabla h_2 (x^+)
\end{aligned}
\right].](/sites/default/files/tex_cache/51e1268796d5b81045795874c60e2f7f.png)
Поскольку вектор ![\left[ 1, \frac{dU}{dx_1}, \frac{dV}{dx_1}\right]](/sites/default/files/tex_cache/e1eb5bdf5f43944ae5763bd6e691b1a2.png) не является нулевым, то из (4.12) следует, что det A = 0. Из этого следует, что вектора-строки
матрицы A должны быть линейно зависимы.
Следовательно, существуют три таких скаляра a, b, c не все равные 0, что
не является нулевым, то из (4.12) следует, что det A = 0. Из этого следует, что вектора-строки
матрицы A должны быть линейно зависимы.
Следовательно, существуют три таких скаляра a, b, c не все равные 0, что
 |
( 4.13) |
Скаляр а не может равняться 0,
так как в соответствии с предположением  и
и  - линейно независимы.
Поэтому после деления (4.13) на a, получим
- линейно независимы.
Поэтому после деления (4.13) на a, получим
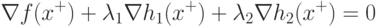 |
( 4.14) |
Таким образом, для задачи минимизации с ограничениями (4.6)
существуют такие 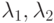 , для которых
справедливо уравнение (4.14) и которые одновременно не обращаются
в нуль. Итак, справедливость условий (4.4) для случая n=3 показана.
, для которых
справедливо уравнение (4.14) и которые одновременно не обращаются
в нуль. Итак, справедливость условий (4.4) для случая n=3 показана.
Таким образом, для отыскания минимума (4.6) при условиях (4.7) необходимо найти стационарную точку функции Лагранжа:
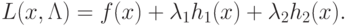
Для того чтобы найти искомые значения 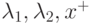 ,
необходимо решить совместно систему уравнений (4.14), (4.5).
С геометрической точки зрения условие (4.14) означает, что
,
необходимо решить совместно систему уравнений (4.14), (4.5).
С геометрической точки зрения условие (4.14) означает, что 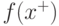 лежит в плоскости, натянутой на векторы
лежит в плоскости, натянутой на векторы 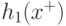 .
.
Теперь рассмотрим общий случай для произвольных n.
Пусть задана задача НП в виде (4.1), (4.2), все функции  , имеют
непрерывные частные производные на множестве R(n).
Пусть S(x) - подмножество множества R(n),
на котором все функции
, имеют
непрерывные частные производные на множестве R(n).
Пусть S(x) - подмножество множества R(n),
на котором все функции 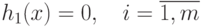 , то есть
, то есть 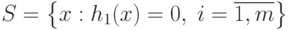 .
Тогда справедлива такая теорема о множителях
Лагранжа.
.
Тогда справедлива такая теорема о множителях
Лагранжа.
Теорема 4.7. Допустим, что существует такая точка x+, в которой достигается относительный экстремум задачи НП (4.1)
при условиях (4.2). Если ранг матрицы ![I = \left[ \frac{\partial h_j(x)}{\partial x_j} \right], \;
i= \overline{1,m}, \; j= \overline{1,n}](/sites/default/files/tex_cache/810b85b735ea9a40027fbb2766e6c075.png) в точке x+ равен m, то существуют m чисел
в точке x+ равен m, то существуют m чисел 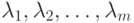 , не все из которых равны нулю одновременно,
при которых
, не все из которых равны нулю одновременно,
при которых
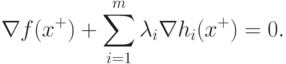 |
( 4.15) |
Эта теорема обосновывает метод множителей Лагранжа, который состоит из следующих шагов.
Находят частные производные 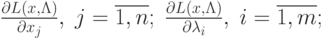
Решают систему уравнений
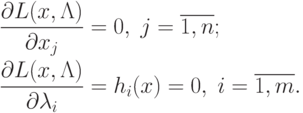 |
( 4.16) |
![x^0 = \left[ x_j^0 \right]](/sites/default/files/tex_cache/e3e6dee32208d39adedddd70a4ac12c2.png) , удовлетворяющие системе (4.16).
, удовлетворяющие системе (4.16).Найденные точки x0 дальше исследуют на максимум (или минимум).