Численные методы решения нелинейных уравнений

Метод Ньютона (метод касательных)

Рассмотренные ранее методы решения нелинейных уравнений являются методами прямого поиска. В них для нахождения корня используется нахождение значения функции в различных точках интервала [a,b].

Метод Ньютона относится к градиентным методам, в которых для нахождения корня используется значение производной.

Дано нелинейное уравнение:

f(x)=0

Найти корень на интервале [a,b] с точностью .

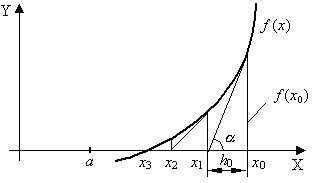
Метод Ньютона основан на замене исходной функции f(x), на каждом шаге поиска касательной, проведенной к этой функции. Пересечение касательной с осью Х дает приближение корня (Рис. 4.8).

Выберем начальную точку x₀=b (конец интервала изоляции). Находим значение функции в этой точке и проводим к ней касательную, пересечение которой с осью Х дает нам первое приближение корня x₁.

Рис. 4.8.

x1 = x0 – h0,

где

Поэтому

В результате итерационный процесс схождения к корню реализуется рекуррентной формулой

( 4.6)

Процесс поиска продолжаем до тех пор, пока не выполнится условие:

( 4.7)

Упростим условие (4.7), исходя из (4.6). Получим:

( 4.8)

Метод обеспечивает быструю сходимость, если выполняется условие:

( 4.9)

т.е. первую касательную рекомендуется проводить в той точке интервала [a,b], где знаки функции f(x₀) и ее кривизны f"(x₀) совпадают.

Схема алгоритма уточнения корня метод Ньютона приведена на рис. 4.9

Рис. 4.9. Схема алгоритма уточнения корня методом Ньютона

Модифицированный метод Ньютона (метод секущих)

В этом методе для вычисления производных на каждом шаге поиска используется численное дифференцирование по формуле:

Тогда рекуррентная формула (4.6) будет иметь вид:

( 4.10)

где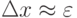

Метод хорд

Метод основан на замене функции f(x) на каждом шаге поиска хордой, пересечение которой с осью Х дает приближение корня.

При этом в процессе поиска семейство хорд может строиться:

а) при фиксированном левом конце хорд, т.е. z=a, тогда начальная точка х₀=b (рис. 4.10а);

б) при фиксированном правом конце хорд, т.е. z=b, тогда начальная точка х₀=a (рис. 4.10б);

Рис. 4.10.

В результате итерационный процесс схождения к корню реализуется рекуррентной формулой:

для случая а)

( 4.11)

для случая б)

( 4.12)

Процесс поиска продолжается до тех пор, пока не выполнится условие

( 4.13)

Метод обеспечивает быструю сходимость, если f(z)f"(z) > 0, т.е. хорды фиксируются в том конце интервала [a,b], где знаки функции f(z) и ее кривизны f"(z) совпадают.

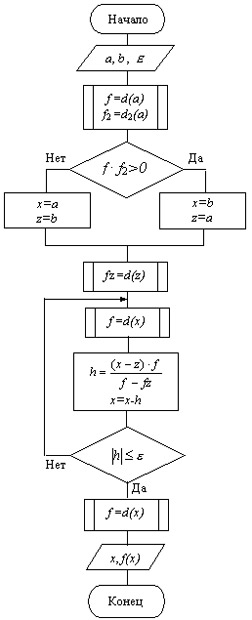
Схема алгоритма уточнения корня методом хорд представлена на рис. 4.11.

увеличить изображение
Рис. 4.11. Схема алгоритма уточнения корня методом хорд