Численное интегрирование
Пояснение. Для некоторых классов функций существуют квадратурные формулы с rN(t) = 0, которые называются точными. Примером такого класса функций являются полиномы
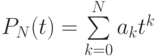
на отрезке [a, b]. Определим на этом отрезке узлы ti, i = 1, … , N и веса ci так, что
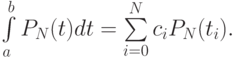
Представим PN(t) в виде интерполяционного полинома

при этом остаточный член интерполяции полинома равен нулю: 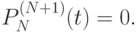
Тогда из предыдущего условия следует
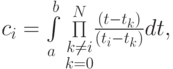
где ci являются базисными функциями полиномов Лагранжа. Квадратурная формула
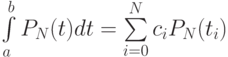
является точной для любого полинома степени N. Оказывается, эта формула может быть точной и для полиномов более высокой степени, а именно, 2N + 1, что используется при построении квадратурных формул Гаусса.
Пусть формула численного интегрирования имеет вид
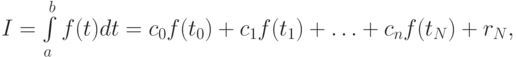
где ci — веса, rN — остаточный член квадратуры.
Положим, что существует многочлен PM(t) степени M > N, для которого квадратурная формула точна, т.е. rN = 0 при f(t) = PM(t):
f(t) = PM(t) = a0 + a1t + a2t2 + ... + aMtM,
где ai — коэффициенты. В этом случае получим

Приравняем выражения в обеих частях равенства при aj:

Получается нелинейная система из M + 1 уравнения с 2(N + 1) неизвестными ci, ti. Отсюда следует, что максимальное значение M есть 2N + 1. Решение этой системы или исследование на его существование и единственность в общем случае затруднительны. Ниже будет рассмотрен пример получения квадратурной формулы Гаусса таким путем для двух узлов.
Гаусс решил эту задачу более простым (в смысле реализации, но не решения!) способом, доказав следующую теорему. Приведем ее без доказательства.
Теорема. Если в качестве узлов ti, i = 0, ..., N в квадратурной формуле используются нули полиномов Лежандра qN + 1(t), а веса ci вычисляются по формулам
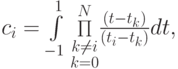
то квадратурная формула
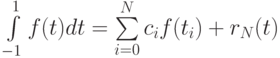
точна для полиномов степени 2N + 1.
Напомним, что полиномы Лежандра образуют ортогональную систему функций на отрезке [- 1; 1]:
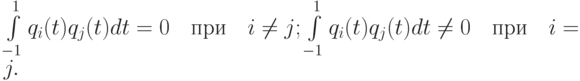
Первые несколько полиномов Лежандра будут

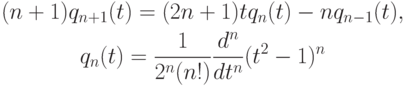
Заметим, что рекуррентные формулы, связывающие три полинома порядка n - 1, n и n + 1 уже встречались для полиномов Чебышева. Такие рекуррентные формулы существуют для всех систем ортогональных полиномов.
Погрешность квадратурной формулы Гаусса на отрезке будет  при этом
при этом ![\xi \in [- 1, 1].](/sites/default/files/tex_cache/7190b065905859ff049bc304a5557c81.png) Для
Для ![\xi \in [a, b]](/sites/default/files/tex_cache/a2d18d95d8e1dd0513eb234c190de1d1.png) формула остаточного члена будет
формула остаточного члена будет  причем коэффициент
причем коэффициент  быстро убывает с ростом N. Здесь
быстро убывает с ростом N. Здесь
![$ \alpha_N = \frac{[(N + 1)!]^4}{\{[2(N + )]!\}^3
[2(N + 1) + 1]} $.](/sites/default/files/tex_cache/3158156b56a5d667af7aa1750ec44684.png)
Формулы Гаусса обеспечивают высокую точность уже при небольшом количестве узлов (от 4 до 10) В этом случае 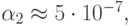

 В практических же вычислениях число узлов составляет от нескольких сотен до нескольких тысяч. Отметим также, что веса квадратур Гаусса всегда положительны, что обеспечивает устойчивость алгоритма
вычисления сумм
В практических же вычислениях число узлов составляет от нескольких сотен до нескольких тысяч. Отметим также, что веса квадратур Гаусса всегда положительны, что обеспечивает устойчивость алгоритма
вычисления сумм 
