Лекция 4:
Численное решение переопределенных СЛАУ. Метод наименьших квадратов
3.3. Задачи
- Для функции
 на отрезке [0,1] построить многочлен F(x) = u0 + u1x среднеквадратичного приближения со скалярными произведениями:
на отрезке [0,1] построить многочлен F(x) = u0 + u1x среднеквадратичного приближения со скалярными произведениями: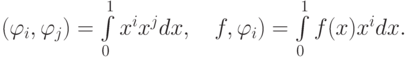
Решение. Введем базисные функции
 и вычислим скалярные произведения
и вычислим скалярные произведения
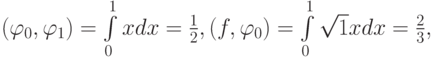
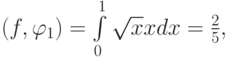
Для вычисления коэффициентов получим СЛАУ
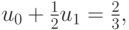

откуда
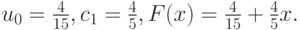
- Получить СЛАУ
c11x + c12y = f1 c22x + c21y = f2,
если она задана в форме метода наименьших квадратов:
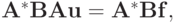 где
где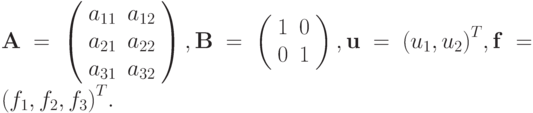
Решить эту систему для случая a11 = a32 = 1, a21 = a12 = 2, a31 = 0, a22 = 1, f1 = 1, f2 = 2, f3 = 1.
Решение. Проведем необходимые вычисления:
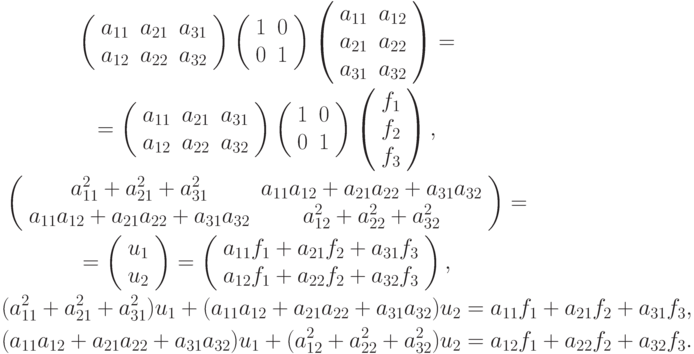
Решение в числах предлагается найти читателям.
- С помощью метода наименьших квадратов найти коэффициенты полинома второй степени f(x) = u0 + u1x + u2x2, если таблица измерений задана
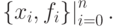
Решение. Переопределенная система уравнений:
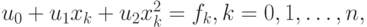
определяет функционал
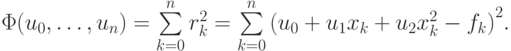
Условия минимума последнего
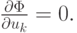
После проведения алгебраических преобразований получим для коэффициентов систему линейных уравнений