Графы
8.4. Эвристический поиск
Декларативный метод, который используется в программе из листинга 8.4, прост, но не эффективен. Пути между заданными парами вершин, которые используются для проверки, кратчайший ли путь найден, могут вычисляться несколько раз. В следующей программе для поиска кратчайших путей применяется более эффективный алгоритм. Кратчайшие из уже найденных путей запоминаются в базе данных. Кроме этого, используется эвристика. Если длина текущего пути уже превышает длину кратчайшего из найденных путей, то текущий путь далее не продлевается, сразу выполняется откат для поиска другого варианта3Пример приведен для версии 7.5. В версии 7.4 вместо выражения not(A in B) должно быть not(list::isMember(A, B)). Вместо A и B в листингах стоят разные переменные..
class facts - graph
arc: (string, string, unsigned).
class facts
minpath: (string*).
mindist : unsigned := 2^30.
class predicates
shortestPath: (string, string, string* [out], unsigned [out])
nondeterm.
path: (string, string, string*, string* [out], unsigned,
unsigned [out]) nondeterm.
setPath: (string*, unsigned).
edge: (string, string, unsigned) nondeterm (i,o,o).
clauses
edge(X, Y, Dist):-
arc(X, Y, Dist);
arc(Y, X, Dist).
shortestPath(Start, Goal, list::reverse(Path), mindist):-
path(Start, Goal, [Start], Path, 0, Dist),
setPath(Path, Dist),
fail;
minPath(Path).
setPath(Path, Dist):-
Dist > mindist, !;
if Dist < mindist then
retractAll(minpath(_)),
mindist := Dist
end if,
assert(minpath(Path)).
path(Goal, Goal, Path, Path, Dist, Dist):- !.
path(V, Goal, CurrPath, Path, CurrDist, Dist):-
edge(V, NextV, D),
CurrDist + D <= mindist,
not(NextV in CurrPath),
path(NextV, Goal, [NextV | CurrPath], Path, CurrDist + D, Dist).
run():-
file::consult("graph.txt", graph),
shortestPath("Москва", "Новосибирск", Path, D),
write(string::concatWithDelimiter(Path, " -> "), " : ", D), nl,
fail;
_ = readLine().
Пример
8.5.
Эвристический поиск кратчайших путей
8.5. Поиск в ширину
Рассмотрим поиск в ширину. В его реализации все пройденные пути собираются в список. Голова этого списка становится текущим путем. В начале поиска этот путь содержит только начальную вершину, а список пройденных путей состоит только из текущего пути. Находятся продолжения текущего пути. Список этих продолжений присоединяется к хвосту списка пройденных путей (если его поставить в начало списка пройденных путей, то получится другая реализация поиска в глубину). В результате получается новый список пройденных путей. Поиск заканчивается, когда голова текущего пути совпадет с конечной вершиной.
При поиске в ширину первым всегда продлевается путь, содержащий наименьшее количество ребер.
Вернемся к графу, изображенному на рис. 8.2 (a). На рис. 8.4 показан результат обхода графа в ширину из вершины  .
.
Построение путей из вершины a, в соответствии с описанным выше алгоритмом поиска в ширину, выполняется следующим образом (см. рис. 8.4):
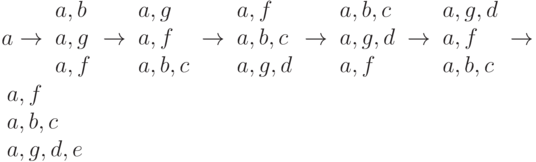
В программе, приведенной ниже, поиск в ширину используется для нахождения путей между заданными вершинами. Как и ранее, пути записываются в список, как в стек, поэтому в конце выполняется операция обращения найденного пути4Пример приведен для версии 7.5. В версии 7.4 вместо выражения not(A in B) должно быть not(list::isMember(A, B)). Вместо A и B в листингах стоят разные переменные..
class facts - graph
arc: (string, string, unsigned).
class predicates
breadthFirst: (string, string) -> string* nondeterm.
path: (string**, string) -> string* nondeterm.
edge: (string, string, unsigned) nondeterm (i,o,o).
clauses
edge(X, Y, Dist):-
arc(X, Y, Dist);
arc(Y, X, Dist).
breadthFirst(Start, Goal) = list::reverse(Path):-
Path = path([[Start]], Goal).
path([[Goal | Path] | _], Goal) = [Goal | Path]:- !.
path([[V | Path] | PathList], Goal) = path(NextPathList, Goal):-
NewPaths = [[NextV, V | Path] ||
edge(V, NextV, _), not(NextV in Path)],
NextPathList = list::append(PathList, NewPaths).
run():-
file::consult("graph.txt", graph),
Path = breadthFirst("Москва", "Новосибирск"),
write(string::concatWithDelimiter(Path, " -> ")), nl,
fail;
_ = readLine().
Пример
8.6.
Поиск в ширину
Если в список помещать пройденные пути вместе с их весом и первым в продлевать путь наименьшего веса, то в результате получится реализация алгоритма "первый лучший". В следующей программе для поиска кратчайшего пути применяется алгоритм "первый лучший". Для хранения пути и его веса используется терм tuple(Path, Dist), из таких термов состоит список, который строит предикат5Пример приведен для версии 7.5. В версии 7.4 вместо выражения not(A in B) должно быть not(list::isMember(A, B)). Вместо A и B в листингах стоят разные переменные. bestFirst.
open core, console, list
class facts - graph
arc: (string, string, unsigned).
class predicates
bestFirst: (string, string) -> tuple{string*, unsigned} nondeterm.
path: (tuple{string*, unsigned}*, string) ->
tuple{string*, unsigned} nondeterm.
edge: (string, string, unsigned) nondeterm (i,o,o).
clauses
edge(X, Y, Dist):-
arc(X, Y, Dist);
arc(Y, X, Dist).
bestFirst(Start, Goal) = tuple(reverse(Path), Dist):-
tuple(Path, Dist) = path([tuple([Start], 0)], Goal).
path([tuple([Goal | Path], Dist) | _], Goal) =
tuple([Goal | Path], Dist):- !.
path([tuple([V | Path], Dist) | PathList], Goal) =
path(NextPathList, Goal):-
NewPaths = [tuple([NextV, V | Path], Dist + D) ||
edge(V, NextV, D), not(NextV in Path)],
NextPathList = sortBy(
{(tuple(_, D1), tuple(_, D2)) = compare(D1, D2)},
append(NewPaths, PathList)).
run():-
file::consult("graph.txt", graph),
tuple(Path, D) = path("Москва", "Новосибирск"),
write(string::concatWithDelimiter(Path, " -> "), " : ", D), nl,
fail;
_ = readLine().
Пример
8.7.
Алгоритм "первый лучший"


