Машина вывода Пролога

2.7. Условные выражения. Знак равенства

Для сравнения термов в языке Visual Prolog используются знаки < ("меньше"), <= ("меньше или равно"), > ("больше"), >= ("больше или равно"), = ("равно"), <> или >< ("не равно"). Сравниваемые термы должны принадлежать одному и тому же домену.

Порядок сложных термов по умолчанию определяется следующим образом: , если . Например,

tuple(5, 8) < tuple(6, 4) и [4, 5] > [1, 2, 3].

Порядок составных термов, домен которых содержит несколько альтернатив, соответствует порядку следования альтернатив в объявлении домена. Например (см. листинг 2.3):

magazine("Наука и жизнь", 6, 2010) > 
    book(author("Чехов", "Антон", "Павлович"), "Избранное",
            edition("Москва", "ЭКСМО", 2012)).

Сравнивать можно только термы, которые не содержат неконкретизированных переменных. Исключение составляет знак равенства.

Знак равенства () используется как для проверки равенства замкнутых термов, так и для означивания свободных переменных в результате процедуры унификации термов. В языке Visual Prolog требуется, чтобы в результате унификации все свободные переменные стали конкретизированными. Свободные переменные могут находиться в любой части равенства. Например, результат вызова подцели

2 = X, tuple(Y, tuple(4, X)) = tuple(3, Z)

имеет вид:

X = 2, Y = 3, Z = tuple(4, 2)

Унификация термов может выполняться с помощью знака двойного равенства ==. В этом случае, если термы не унифицируемы, возбуждается исключение.

Примером переменной, которая всегда неконкретизирована, является анонимная переменная.

2.8. Отрицание

Данный параграф посвящен проблеме отрицания в языке Пролог.

Рассмотрим программу:

супруг("Иван", "Анна").

мужчина("Иван").
мужчина("Петр").
мужчина("Степан").

С декларативной точки зрения цель не следует логически из программы, она не принадлежит ее минимальной модели. С другой стороны, это же утверждение верно и для цели . В логическом программировании принято "допущение о замкнутости мира" , в предположении которого цель 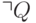Q логически следует из программы, если цель не следует логически из программы (ее минимальной модели). С процедурной точки зрения такая проблема в общем случае алгоритмически неразрешима.

Для выражения отрицания в языке Пролог используется предикат not/1. Из приведенной выше программы следует, что неженатыми мужчинами, которых можно найти с помощью запроса

?- мужчина(X), not(супруг(X, _)).

являются Петр и Степан, и только они.

Для вычисления целей с отрицаниями применяется правило "отрицания как неудачи" (Not by Failure) — метод SLDNF-резолюции [7]. Пусть 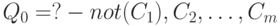— запрос к программе, дерево SLD-резолютивных вычислений запроса 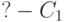конечно и все его ветви являются тупиковыми. Тогда SLDNF-резольвентой запроса 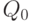является запрос 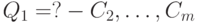, полученный из 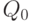с помощью пустой подстановки. Если же вычисление запроса 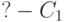успешно, то запрос 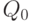терпит неуспех.

Таким образом, цель not(p) успешна в точности тогда, когда цель p неуспешна. При вычислении цели not(p) вызывается цель p. Если цель p имеет хотя бы одно решение и дерево вычислений этой цели конечно, то цель not(p) считается неуспешной. В противном случае, если дерево вычислений цели p конечно, но все его ветви — тупиковые, цель not(p) считается успешной. Откат под знаком отрицания после достижения цели не производится (для другого доказательства цели), значения из-под него не возвращаются. Под знаком отрицания неконкретизированные переменные считаются анонимными.

Упражнение 4.

Сформулируйте запрос к программе "Родственные отношения" (см. листинг 1.2): найти незамужних сестер (известных программе), т. е. незамужних женщин, у которых есть сестры или братья (для этого в программе нужно определить отношение "сестра"). Найдите ответ на этот запрос

• в PIE;
• в Visual Prolog.

Следующая программа посвящена вычислению возраста студентов и определению самых юных из них. Студент — самый юный, если моложе его по возрасту никого нет. Возраст определяется как разность между текущим годом и годом рождения. Сведения о датах рождения хранятся в базе данных. Текущий год считывается автоматически из системы.

domains
    date = date(integer День, integer Месяц, integer Год).

class facts
    dateOfBirth: (string Имя, date ДатаРождения).
clauses
    dateOfBirth("Елизавета", date(2, 5, 1999)).
    dateOfBirth("Тимофей", date(10, 10, 2000)).
    dateOfBirth("Даниил", date(25, 2, 2000)).
    % … 

class predicates
    age: (string Name, integer Age) nondeterm (o,o).
    youngestPerson: (string Name, integer Age) nondeterm (o,o).
clauses
    age(Name, Age):-
        Time = time::new(), 
        Time:getDate(CurrentYear, _M, _D),
        dateOfBirth(Name, date(_, _, YearOfBirth)),
        Age = CurrentYear - YearOfBirth.

    youngestPerson(Name, Age):-
        age(Name, Age),
        not((age(_, X), X < Age)).

    run():-
        youngestPerson(Name, Age),
            write(Name, " - ", Age), nl,
        fail;
        _ = readLine().

Для определения текущего года в программе создается объект класса time. Переменная Time хранит указатель на объект класса time. Методы объектов вызываются следующим образом: пишется указатель на объект, ставится знак двоеточия, затем пишется имя предиката. Предикат getDate/3 возвращает текущую дату (установленную на компьютере) — год, месяц и день.

Упражнение 5.

1. Измените программу из листинга 2.5 так, чтобы текущий год вычислялся только один раз.
2. Дополните программу отношением month/2 и выведите названия месяцев, в которые родились студенты.

В следующей программе отрицание используется для определения более сложных родственных отношений, чем те, что рассматривались ранее.

class facts - relatives
    parent: (string Родитель, string Ребенок).
    spouse: (string Муж, string Жена).
    male: (string).
    female: (string).

class predicates
    sister: (string Сестра, string Чья) nondeterm (o,o).
    bloodSister: (string Сестра, string Чья) nondeterm (o,o).
    halfSister: (string Сестра, string Чья) nondeterm (o,o).
    haveCommonFather: (string, string) nondeterm anyflow.
    haveCommonMother: (string, string) nondeterm anyflow.
clauses
    sister(X, Y):-
        bloodSister(X, Y);
        halfSister(X, Y).

    bloodSister(X, Y):-
        female(X),
        haveCommonFather(X, Y),
        haveCommonMother(X, Y).

    halfSister(X, Y):-
        female(X),
        (haveCommonFather(X, Y), 
        not(haveCommonMother(X, Y));
        haveCommonMother(X, Y), 
        not(haveCommonFather(X, Y))).

    haveCommonFather(X, Y):-
        male(Z),
        parent(Z, X),
        parent(Z, Y),
        X <> Y.

    haveCommonMother(X, Y):-
        female(Z),
        parent(Z, X),
        parent(Z, Y),
        X <> Y.

    run():-
        file::consult("family.txt", relatives),
        sister(X, Y),
            write(X, " - сестра для - ", Y), nl,
        fail;
        _ = readLine().

Упражнения

1. Найдите с помощью программы "Библиотека" ответы на запросы:

   • Какие журналы за позапрошлый год имеются в библиотеке? (Текущий год определяется с помощью предиката getDate/3).
   • Найдите самую старую по году издания литературу.

2. Найдите ответ на вопросы с помощью программы "Иностранные языки":

   • кто владеет только английским и немецким языками;
   • кто владеет ровно одним иностранным языком?

   Дополните программу новыми фактами.

3. Определите через базовые отношения "родитель", "мужчина", "женщина" и "супруг" следующие отношения:

   • "племянник";
   • "двоюродная сестра";
   • "сват"

   (см. листинг 2.6).

4. Напишите программу, которая выводит названия месяцев

   • с начала года, предшествующие заданному месяцу;
   • до конца года, следующие за данным месяцем.

5. Напишите программу, которая из набора точек с целыми координатами на плоскости выбирает пары ближайших к друг другу точек. Каждая точка хранится в отдельном факте вида:

   point(pnt(-1, 3)).
   

6. Приведите пример таких фактов, определяющих отношения "родитель" и "мужчина", чтобы запросы

   male(X), parent(X, _)  и  male(X), not(not(parent(X, _)))
   

   имели разный набор решений.

7. Найдите процедурное значение программы "Птицы" (листинг 1.1).

8. Постройте дерево SLD-резолютивных вычислений для запроса ?- родитель(X, Y), родитель(Y, Z) к программе из листинга 2.1.