|
Где можно посмотреть информацию о физических ограничениях на значения характеристик компьютеров |
Наноэлектронная элементная база информатики на основе графена
Графен и его физические свойства
Структура графена
Еще одной интересной, ранее неизвестной, формой существования углерода оказался графен (англ. graphene) – однослойная пленка из атомов углерода, находящихся в состоянии 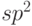 -гибридизации. Ее можно рассматривать также как один отделенный слой графита (
рис.
7.1).
-гибридизации. Ее можно рассматривать также как один отделенный слой графита (
рис.
7.1).

Рис. 7.1. Слева – структурная модель пленки графена. Справа – микрофотография следа от графитового карандаша на окисленной пластине кремния при увеличении 2000х
В течение многих десятилетий исследователям никак не удавалось сформировать такую пленку или отделить ее от графита, и временами даже теоретически "обосновывалась" невозможность ее самостоятельного существования. Тем не менее, в 2004 г. пленку графена удалось не только отделить, но и экспериментально исследовать ее свойства. Эти пионерские исследования отмечены Нобелевской премией за 2010 г. Позднее оказалось, что даже при рисовании обычным графитовым карандашом такие пленки иногда встречаются в отделившихся от графита чешуйках. Просто они настолько малы, тонки и прозрачны, что их очень трудно увидеть, даже в наилучший оптический микроскоп.
Только теперь с помощью виртуозных интерференционных методик их уже сумели наблюдать в оптических микроскопах высокой разрешающей способности. На рис. 7.1 справа показана микрофотография одного из участков следа от графитового карандаша, оставленного на пластине кремния с окислом толщиной 300 нм. На ней можно увидеть отделившиеся от графита чешуйки разной толщины, тончайшая из которых – одноатомный слой графита. Это и есть пленка графена.
Структурная модель графена показана на
рис.
7.1 слева. Атомы углерода, изображенные в виде шариков, выстроены в правильную двумерную гексагональную решетку. В ней они удерживаются с помощью ковалентных  -связей, образованных тремя гибридными
-связей, образованных тремя гибридными 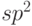 –орбиталями каждого атома углерода, и дополнительно с помощью
–орбиталями каждого атома углерода, и дополнительно с помощью  -связей, образованных благодаря перекрытию рZ–орбиталей соседних атомов углерода (см.
"Наноэлектронная элементная база информатики на основе графена"
,
рис.
7.4). Тонкие "покрывала" из плазмы
-связей, образованных благодаря перекрытию рZ–орбиталей соседних атомов углерода (см.
"Наноэлектронная элементная база информатики на основе графена"
,
рис.
7.4). Тонкие "покрывала" из плазмы  -электронов, напоминающие слой тумана над водой, находятся с обеих сторон пленки. И эти
-электронов, напоминающие слой тумана над водой, находятся с обеих сторон пленки. И эти  -электроны (по одному от каждого атома) принадлежат не отдельным атомам или парам соседних атомов углерода, а "расплываются" по всей пленке, "обобществляются", образуя легкую двумерную электронную плазму.
-электроны (по одному от каждого атома) принадлежат не отдельным атомам или парам соседних атомов углерода, а "расплываются" по всей пленке, "обобществляются", образуя легкую двумерную электронную плазму.
Физические свойства графена
Благодаря такой удачной "конструкции", пленки графена удивительно прочны и упруги. Модуль Юнга у них – порядка 1 ТПа, предел прочности – 130 ГПа (по сравнению со сталью, у которой модуль Юнга составляет 210 ГПа, а предел прочности около 600 МПа). Несмотря на свою предельно малую толщину (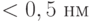 ), они настолько плотны, что не пропускают сквозь себя даже атомы гелия, способные проникать, например, сквозь фольгу из металла. О легкости пленок графена дает представление то, что лишь один грамм графена, будучи целостной пленкой, накрыл бы площадь 2600 м2 – целое футбольное поле.
), они настолько плотны, что не пропускают сквозь себя даже атомы гелия, способные проникать, например, сквозь фольгу из металла. О легкости пленок графена дает представление то, что лишь один грамм графена, будучи целостной пленкой, накрыл бы площадь 2600 м2 – целое футбольное поле.
Графен имеет очень высокую теплопроводность – порядка 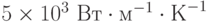 , что в сочетании с высокой электропроводностью обеспечивает возможность прохождения электрического тока в миллион раз превосходящего максимально возможный ток в пленках меди.
, что в сочетании с высокой электропроводностью обеспечивает возможность прохождения электрического тока в миллион раз превосходящего максимально возможный ток в пленках меди.
Графен почти не поглощает видимый свет, коэффициент его пропускания превышает 97%. Комплексный показатель преломления графена для видимой области спектра равен приблизительно 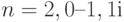 .
.
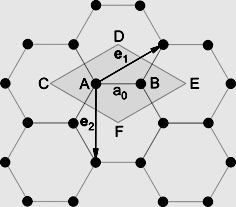
Элементарной ячейкой гексагональной решетки графена является выделенный на рис. 7.2 ромб CDEF, в состав которого входят два атома углерода (A и B).
Всю решетку – т.н. "двумерный кристалл" – можно получить трансляцией этой ячейки на векторы
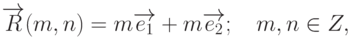 |
( 8.1) |
 и
и 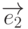 – элементарные векторы трансляции. Расстояние между центрами соседних атомов углерода составляет 0,1415 нм, а длина элементарных векторов трансляции – 0,245 нм.
– элементарные векторы трансляции. Расстояние между центрами соседних атомов углерода составляет 0,1415 нм, а длина элементарных векторов трансляции – 0,245 нм.Энергетический спектр электронов в графене
Квантово-механический расчет волновых функций электронов в такой двумерной гексагональной решетке, впервые сделанный еще в середине ХХ в., когда графен был только теоретической моделью, показал, что в графене, как и в графите, в энергетическом спектре  -электронов нет запрещенной зоны энергий, как в полупроводниках или в изоляторах. Валентная зона и зона проводимости в графене касаются. Поэтому, графен, как и графит, является полуметаллом. Зависимость разрешенных значений энергии
-электронов нет запрещенной зоны энергий, как в полупроводниках или в изоляторах. Валентная зона и зона проводимости в графене касаются. Поэтому, графен, как и графит, является полуметаллом. Зависимость разрешенных значений энергии  -электронов в графене от величины и направления их волнового вектора
-электронов в графене от величины и направления их волнового вектора 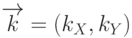 показана на
рис.
7.3. Вдоль вертикали здесь отложена энергия, вдоль осей абсцисс и ординат – соответствующие проекции волнового вектора электрона
показана на
рис.
7.3. Вдоль вертикали здесь отложена энергия, вдоль осей абсцисс и ординат – соответствующие проекции волнового вектора электрона 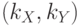 .
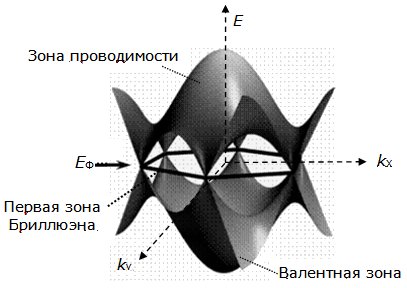
Правильный шестиугольник, ограничивающий первую зону Бриллюэна, выделен жирными черными отрезками. Он расположен относительно оси аппликат на уровне энергии Ферми. Поверхности, описывающие структуру валентной зоны и зоны проводимости, касаются в вершинах шестиугольника. Эти точки называют "точками Дирака". При температурах, близких к абсолютному нулю, валентная зона полностью заполнена электронами, а зона проводимости пуста. При повышенных температурах согласно распределению Ферми–Дирака некоторая часть электронов переходит в зону проводимости, а в валентной зоне остаются "дырки". Это и предопределяет достаточно высокую электропроводность графена при комнатных температурах. Концентрация носителей заряда в точках Дирака при таких температурах составляет приблизительно 5*1016 м–2.
.
Правильный шестиугольник, ограничивающий первую зону Бриллюэна, выделен жирными черными отрезками. Он расположен относительно оси аппликат на уровне энергии Ферми. Поверхности, описывающие структуру валентной зоны и зоны проводимости, касаются в вершинах шестиугольника. Эти точки называют "точками Дирака". При температурах, близких к абсолютному нулю, валентная зона полностью заполнена электронами, а зона проводимости пуста. При повышенных температурах согласно распределению Ферми–Дирака некоторая часть электронов переходит в зону проводимости, а в валентной зоне остаются "дырки". Это и предопределяет достаточно высокую электропроводность графена при комнатных температурах. Концентрация носителей заряда в точках Дирака при таких температурах составляет приблизительно 5*1016 м–2.
Очень интересной особенностью графена является то, что вблизи точек соприкосновения энергетических зон дисперсионное отношение (т.е. зависимость между энергией и волновым вектором электрона) оказалось линейным:

Это означает, что в таких состояниях и электроны проводимости, и "дырки" в графене имеют нулевую эффективную массу. Т.е. они не могут быть неподвижными, а все время перемещаются со "скоростью Ферми", которая в графене составляет примерно 106 м/с, то есть является уже релятивистской. Этим обусловлены очень высокая подвижность носителей электрического заряда в графене, минимум на 2 порядка превышающая их подвижность в кремнии, и "баллистический" характер их движения вдоль пленки. Длина свободного пробега электронов проводимости и дырок в графене при комнатных температурах превышает 1 мкм. Но не надо забывать, что как "дырки", так и "электроны проводимости" являются в данном случае "квазичастицами". А на самом деле речь идет о коллективном движении двумерной электронной плазмы.
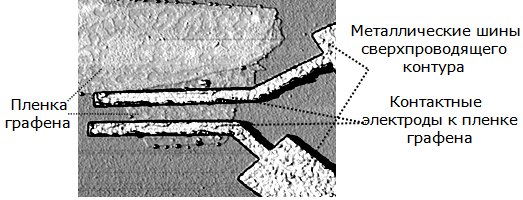
Оказалось, что при низких температурах сквозь графен могут свободно перемещаться не только электроны проводимости, но и куперовские пары электронов (см. "Свойства молекул, лежащие в основе молекулярной элементной базы информатики" ). На рис. 7.4, например, показана пленка графена, к которой присоединены электроды замкнутого сверхпроводящего контура. Расстояние между электродами составляет приблизительно 300 нм. При низких температурах в сверхпроводящем контуре с переходом через пленку графена может протекать незатухающий электрический сверхпроводящий ток. Имеются ли какие-нибудь преимущества у сквидов с таким (графеновым) переходом Джозефсона, покажут дальнейшие исследования.