|
Здравствуйте Владимир (Ефименко). Я обучаюсь по программе повышения квалификации "Наноэлектронная элементная база информатики на основе полупроводников и ферромагнетиков". У меня проблема с тестом № 2 (к лекции № 2) по этой программе. Я несколько раз пытался пройти этот тест, но больше 50 баллов набрать не удаётся, хотя я всё делаю в соответствии сматериалом лекции. В заданиях этого теста есть ошибки, которые видны невооружённым глазом. Обращаюсь к Вам как к инспектору этой программы повышения квалификации. Найдите возможность исправить ошибки в тесте № 2. Из-за остановки на этом тесте я не могу двигаться дальше, а у меня очень ограниченное время на освоение этой программы. Заранее благодарен Вам за внимание к моим проблемам и помощь. |
Качественные изменения свойств при переходе к наноразмерным элементам
Введение
При переходе от микроэлектроники к наноэлектронике произошли качественные изменения не только в методах визуализации элементов интегральных схем, в методах их изготовления, но и существенные количественные и качественные изменения в свойствах таких элементов. Возникла потребность в изменении теоретических моделей, которые их описывают, и в разработке новых методов их проектирования, расчета и моделирования.
Общая направленность изменений в свойствах элементов состоит в том, что уменьшается удельный вес макроскопических взаимодействий (например, сводится практически к нулю роль сил тяготения) и вместе с тем возрастает удельный вес атомно-молекулярных взаимодействий (взаимодействий молекул, атомов, электронов и квазичастиц), хаотического теплового движения. Возрастает роль поверхностных явлений и поверхностных электронных состояний. Если приповерхностная область элемента электронной схемы составляет 3-5 атомных слоев (~1 нм), то при среднем размере элементов, скажем, 6 мкм приповерхностная область составляет лишь 0,1% всего объема элемента. При размерах элементов около 60 нм приповерхностная область составляет уже 10% объема, а при размерах около 20 нм – уже свыше 30% объема элемента.
Особенно значительные, качественные изменения наблюдаются тогда, когда размеры элементов становятся сравнимы или меньше одного из характерных физических параметров, имеющего размерность длины. Такие качественные изменения называют "размерными эффектами".
Изменения во взаимодействии наночастиц со светом
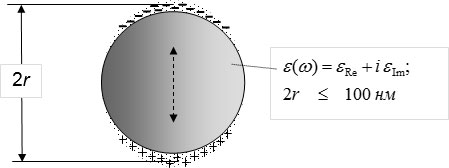
Первым характерным физическим параметром, который стал сравним с размерами элементов при переходе их в нанометровый диапазон, является длина волны света. Для видимого света она составляет 400–700 нм. Нанообъекты с такими размерами взаимодействуют со светом уже не так, как макрообъекты из такого же самого материала. Особенно это заметно на наночастицах некоторых металлов. Электронная плазма металлических наночастиц ( рис. 3.1) способна к вынужденным колебаниям с оптическими частотами до 1016 Гц.
Поскольку размеры наночастиц еще значительно превосходят размеры атомов и расстояния между атомами в металле (~0,1 нм), то наночастицы все еще можно характеризовать такой макроскопической величиной, как диэлектрическая постоянная. В общем случае она существенно зависит от частоты и является комплексной величиной
 |
( 3.1) |
 – круговая частота внешнего электромагнитного поля;
– круговая частота внешнего электромагнитного поля; 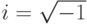 – мнимая единица. Действительная часть диэлектрической постоянной
– мнимая единица. Действительная часть диэлектрической постоянной 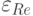 , которая у металлов обычно велика и отрицательна, математически описывает тот физический факт, что внешнее электрическое поле вызывает в металле смещение электронов проводимости в сторону, противоположную направлению поля. Вследствие этого наблюдается явление поляризации – наведенное электрическое поле, направленное навстречу внешнему, внутри металла практически полностью компенсирует внешнее поле. Мнимая же часть комплексной диэлектрической постоянной
, которая у металлов обычно велика и отрицательна, математически описывает тот физический факт, что внешнее электрическое поле вызывает в металле смещение электронов проводимости в сторону, противоположную направлению поля. Вследствие этого наблюдается явление поляризации – наведенное электрическое поле, направленное навстречу внешнему, внутри металла практически полностью компенсирует внешнее поле. Мнимая же часть комплексной диэлектрической постоянной 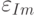 характеризует скорость диссипации энергии внешнего переменного электромагнитного поля в металле (потери на выделение тепла).
характеризует скорость диссипации энергии внешнего переменного электромагнитного поля в металле (потери на выделение тепла).В зависимости от размеров, формы и особенностей частотного поведения диэлектрической постоянной 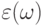 наночастицы имеют характерные резонансные частоты колебаний плазмы (
наночастицы имеют характерные резонансные частоты колебаний плазмы (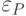 ). Эффективное сечение
). Эффективное сечение 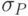 взаимодействия наночастицы с электромагнитной волной на резонансной частоте описывается выражением
взаимодействия наночастицы с электромагнитной волной на резонансной частоте описывается выражением
![\frac{\sigma_P}{S}=\frac{8\pi r}{3\lambda}*\frac{[1-\varepsilon_{Re}]^2}{\varepsilon_{Im}},](/sites/default/files/tex_cache/a6ff6e3d58c0d9a259e427d4524ed5a6.png) |
( 3.2) |
 – площадь поперечного сечения наночастицы плоскостью, перпендикулярной к направлению распространения волны;
– площадь поперечного сечения наночастицы плоскостью, перпендикулярной к направлению распространения волны;  – радиус наночастицы в этой плоскости;
– радиус наночастицы в этой плоскости;  – длина волны в вакууме. Поскольку у некоторых металлов, в частности у золота, серебра, меди и др., мнимая часть
– длина волны в вакууме. Поскольку у некоторых металлов, в частности у золота, серебра, меди и др., мнимая часть 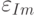 мала, намного меньше
мала, намного меньше 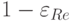 , то сечение взаимодействия таких наночастиц со светом оказывается намного больше, чем их геометрическое сечение. И поэтому на своих резонансных частотах наночастицы таких металлов поглощают и рассеивают свет намного сильнее, чем даже молекулы наилучших органических красителей.
, то сечение взаимодействия таких наночастиц со светом оказывается намного больше, чем их геометрическое сечение. И поэтому на своих резонансных частотах наночастицы таких металлов поглощают и рассеивают свет намного сильнее, чем даже молекулы наилучших органических красителей.Благодаря очень сильной поляризации наночастицы из металла являются также отличными усилителями переменного электромагнитного поля. Коэффициент усиления напряженности электрического поля света в окрестности наночастицы описывается формулой
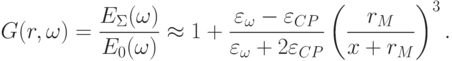 |
( 3.3) |
Здесь 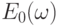 – амплитуда колебаний электрического вектора внешнего электромагнитного поля на частоте
– амплитуда колебаний электрического вектора внешнего электромагнитного поля на частоте  ;
; 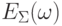 – амплитуда колебаний электрического вектора суммарного поля (внешнее поле плюс поле поляризации наночастицы);
– амплитуда колебаний электрического вектора суммарного поля (внешнее поле плюс поле поляризации наночастицы); 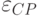 – диэлектрическая постоянная среды, в которой находится наночастица;
– диэлектрическая постоянная среды, в которой находится наночастица; 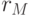 – радиус наночастицы;
– радиус наночастицы;  – расстояние от поверхности наночастицы до точки наблюдения. При приближении к частоте, при которой
– расстояние от поверхности наночастицы до точки наблюдения. При приближении к частоте, при которой 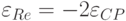 , знаменатель в правой части выражения (3.3) становится минимальным (равняется
, знаменатель в правой части выражения (3.3) становится минимальным (равняется 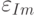 ), и коэффициент усиления электромагнитного поля резко возрастает.
Это явление называют локализованным плазмонным резонансом. Оно особенно выражено у наночастиц золота и серебра, у которых величина
), и коэффициент усиления электромагнитного поля резко возрастает.
Это явление называют локализованным плазмонным резонансом. Оно особенно выражено у наночастиц золота и серебра, у которых величина 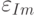 на резонансной частоте мала. Электромагнитное поле света наночастицами из таких металлов возле их поверхности усиливается в десятки раз.
на резонансной частоте мала. Электромагнитное поле света наночастицами из таких металлов возле их поверхности усиливается в десятки раз.
"Классические" размерные эффекты
Принципиально важным характерным физическим параметром является длина волны де Бройля ( ) носителей электрического заряда. В лекции 1 мы уже привели формулу (1.1) для расчета длины волны свободных электронов, ускоренных электрическим полем. Для носителей заряда в металлах, полупроводниках и в диэлектриках в этой формуле массу электрона m надо заменить на т. н. "эффективную массу"
) носителей электрического заряда. В лекции 1 мы уже привели формулу (1.1) для расчета длины волны свободных электронов, ускоренных электрическим полем. Для носителей заряда в металлах, полупроводниках и в диэлектриках в этой формуле массу электрона m надо заменить на т. н. "эффективную массу" 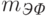 , а кинетическую энергию
, а кинетическую энергию 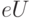 электронов, ускоренных разностью потенциалов
электронов, ускоренных разностью потенциалов  , – на среднюю энергию теплового движения носителей заряда (
, – на среднюю энергию теплового движения носителей заряда (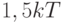 ). Тогда получаем выражение
). Тогда получаем выражение

 и
и  – постоянные Планка и Больцмана (соответственно
– постоянные Планка и Больцмана (соответственно 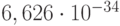 кг*м2/с и
кг*м2/с и 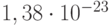 Дж/К или
Дж/К или 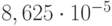 эВ/К),
эВ/К),  – абсолютная температура. Для электронов проводимости в кремнии, эффективная масса которых приблизительно равна массе покоя свободного электрона
– абсолютная температура. Для электронов проводимости в кремнии, эффективная масса которых приблизительно равна массе покоя свободного электрона 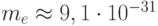 кг, при комнатной температуре по указанной формуле можно рассчитать среднюю длину волны де Бройля
кг, при комнатной температуре по указанной формуле можно рассчитать среднюю длину волны де Бройля 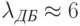 нм. Электроны проводимости в арсениде галлия, эффективная масса которых
нм. Электроны проводимости в арсениде галлия, эффективная масса которых 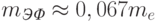 , при комнатной температуре имеют среднюю длину волны де Бройля
, при комнатной температуре имеют среднюю длину волны де Бройля 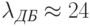 нм.
нм.Качественные изменения, которые наблюдаются при уменьшении размеров элементов в условиях, когда эти размеры превосходят  , называют классическими размерными эффектами, а когда размеры становятся меньше
, называют классическими размерными эффектами, а когда размеры становятся меньше  , – то квантовыми размерными эффектами.
, – то квантовыми размерными эффектами.
Приведем несколько примеров классических размерных эффектов. Рассмотрим провод круглого сечения ( рис. 3.2, слева). Величина его электрического сопротивления, как известно, задается формулой
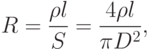 |
( 3.5) |
 – удельное сопротивление,
– удельное сопротивление,  – длина провода,
– длина провода,  – его диаметр. Если все размеры провода уменьшить в
– его диаметр. Если все размеры провода уменьшить в  раз (это называют коэффициентом масштабирования), то его электрическое сопротивление возрастет в
раз (это называют коэффициентом масштабирования), то его электрическое сопротивление возрастет в  раз. График зависимости сопротивления провода от коэффициента масштабирования показан справа. Через
раз. График зависимости сопротивления провода от коэффициента масштабирования показан справа. Через 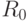 здесь обозначено сопротивление отрезка провода при
здесь обозначено сопротивление отрезка провода при  . Как видно, зависимость эта является линейной лишь до определенных пределов.
. Как видно, зависимость эта является линейной лишь до определенных пределов.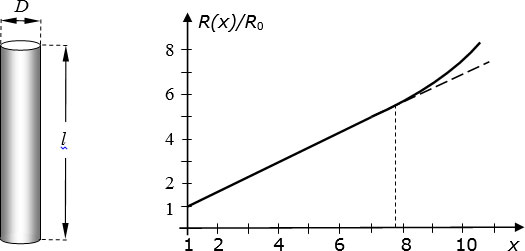
Рис. 3.2. Слева – геометрические размеры провода. Справа – зависимость электрического сопротивления провода от коэффициента масштабирования
Чтобы объяснить это, вспомним физическую природу электрического сопротивления. Оно является следствием рассеяния носителей электрического заряда на неоднородностях кристаллической решетки (на ее дефектах, примесях, фононах). Среднее расстояние между рассеяниями называют "свободным пробегом". Так вот, когда геометрические размеры провода становятся меньше длины свободного пробега, характер рассеяния носителей заряда и переноса электрического заряда вдоль провода качественно меняются. Удельное сопротивление  перестает уже быть постоянной величиной и начинает возрастать с уменьшением размеров – из-за уменьшения длины свободного пробега.
перестает уже быть постоянной величиной и начинает возрастать с уменьшением размеров – из-за уменьшения длины свободного пробега.
Удельное сопротивление  перестает быть постоянной величиной также при уменьшении толщины металлической пленки. Когда толщина пленки становится меньше примерно 100 нм (примерная длина свободного пробега электронов проводимости в металле), удельное сопротивление возрастает, хотя материал пленки остается тем же и имеет такую же структуру. Это – тоже классический размерный эффект.
перестает быть постоянной величиной также при уменьшении толщины металлической пленки. Когда толщина пленки становится меньше примерно 100 нм (примерная длина свободного пробега электронов проводимости в металле), удельное сопротивление возрастает, хотя материал пленки остается тем же и имеет такую же структуру. Это – тоже классический размерный эффект.
Аналогично и в случае транзисторов. Когда размер активной области транзистора становится меньше длины свободного пробега носителей заряда, то изменяется характер переноса заряда сквозь эту область (с т.н. "диффузионного" на "баллистический"), и соответственно меняются характеристики транзистора.
Еще один пример классических размерных эффектов – это поведение элементов из ферромагнитного материала при изменениях внешнего магнитного поля. В массивном материале поведение это практически не зависит от направления магнитного поля. А вот в тонких пленках ферромагнитных материалов, когда толщина пленки становится порядка и меньше размера магнитных доменов, то уже наблюдается значительная магнитная анизотропия: в магнитном поле, параллельном плоскости пленки, она ведет себя по-иному, чем в магнитном поле, направленном перпендикулярно к этой плоскости. Когда все размеры ферромагнитного элемента (например, ячейки памяти) становятся порядка размеров домена, то весь элемент в целом начинает вести себя как единый домен.