|
Добрый день!
Скажите, пожалуйста,планируется ли продолжение курсов по нанотехнологиям? Спасибо, Евгений
|
Термальный синтез микропрограмм алгоритмически ориентированных МКМД-бит-потоковых субпроцессоров
5.3. Термальный синтез алгоритмически ориентированного субпроцессора подстановки данных со встроенными PD-ассоциативными конструкциями
В поток-инструкции 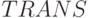 с подстановкой в фазе чтения (рис. 5.7) используется PD -ассоциативный блок
с подстановкой в фазе чтения (рис. 5.7) используется PD -ассоциативный блок 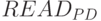 , который обеспечивает поступление сигнала "чтение" (
, который обеспечивает поступление сигнала "чтение" (  - рис. 5.7-б) на выходные вентили FIFO -регистров в порядке, отвечающем реализуемой подстановке.
- рис. 5.7-б) на выходные вентили FIFO -регистров в порядке, отвечающем реализуемой подстановке.
Основная особенность 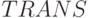 со встроенными PD -ассоциативными блоками состоит в том, что в них удается совместить во времени этапы реализации слов-инструкций
со встроенными PD -ассоциативными блоками состоит в том, что в них удается совместить во времени этапы реализации слов-инструкций 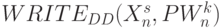 и
и 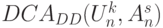 . В этом случае линейная последовательность слов-инструкций принимает вид:
. В этом случае линейная последовательность слов-инструкций принимает вид: 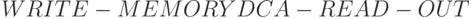 . Здесь перестановка порядка выполнения слов-инструкций
. Здесь перестановка порядка выполнения слов-инструкций 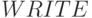 и
и 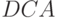 сопровождается зеркальным отражением их топологических схем по отношению к вертикальной оси (ср. рис. 5.6 и рис. 5.7).
сопровождается зеркальным отражением их топологических схем по отношению к вертикальной оси (ср. рис. 5.6 и рис. 5.7).
В результате из (5.1)-(5.5) исключается функциональная задержка в  тактов на дешифрацию, а сами преобразования принимают вид:
тактов на дешифрацию, а сами преобразования принимают вид:
-
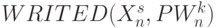 - выходы бит-процессоров 4-го столбца рис. 5.7-а:
- выходы бит-процессоров 4-го столбца рис. 5.7-а: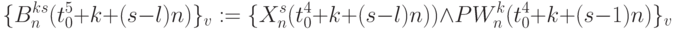
( 5.7) где:
-
 такта - начальная задержка
такта - начальная задержка 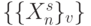 до входа
до входа  -й слов-инструкции
-й слов-инструкции 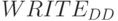 ;
; -
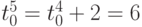 тактов и
тактов и  ;
; -
 - эквивалентна по содержимому
- эквивалентна по содержимому 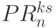 в (5.4).
в (5.4).
-
- 2.
 - выходы "монтажного ИЛИ" бит-процессоров 4-го столбца рис. 5.7-а:
- выходы "монтажного ИЛИ" бит-процессоров 4-го столбца рис. 5.7-а: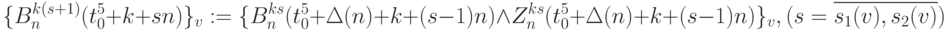
( 5.8) -
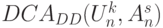 - выходы каналов АЛУ бит-процессоров 7-го столбца рис. 5.6-а и 1-го столбца при зеркальном отражении для рис. 5.7:
- выходы каналов АЛУ бит-процессоров 7-го столбца рис. 5.6-а и 1-го столбца при зеркальном отражении для рис. 5.7: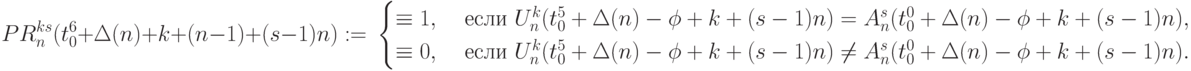
( 5.9)
увеличить изображение
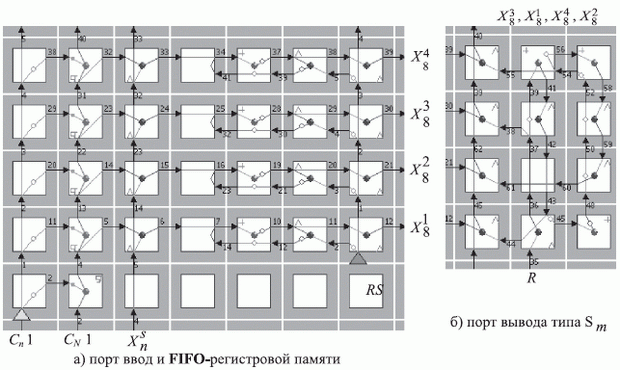
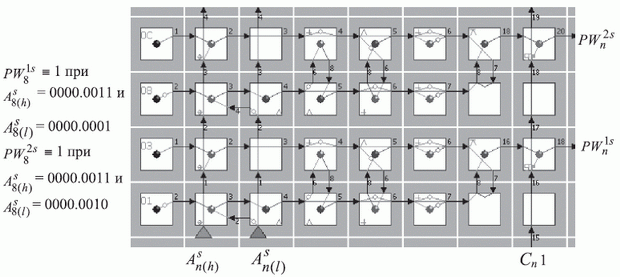
Рис. 5.7. Топологическая схема микропрограммы TRANS_DD с подстановкой при чтениигде
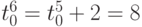 тактов,а
тактов,а 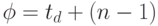 - совмещение во времени этапов записи и дешифрации потоков
- совмещение во времени этапов записи и дешифрации потоков  и
и 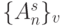 , в которых знача-щие части смещены друг по отношению к другу на
, в которых знача-щие части смещены друг по отношению к другу на  тактов, то есть считается, что в потоке
тактов, то есть считается, что в потоке 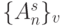 первые
первые  тактов - "нули" а остальные
тактов - "нули" а остальные 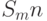 тактов - значащие, а в потоке
тактов - значащие, а в потоке  - наоборот.
- наоборот. -
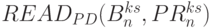 - выходы каналов АЛУ бит-процессоров 1-го столбца рис. 5.7-б:
- выходы каналов АЛУ бит-процессоров 1-го столбца рис. 5.7-б: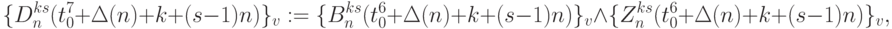
( 5.10) где:
-
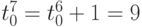 тактов, а
тактов, а  ;
; -
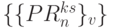 - поток управляющих операндов, который формируется в данном случае бит-процессорами 2-го и 3-го столбцов рис. 5.7-б и имеет циклический по
- поток управляющих операндов, который формируется в данном случае бит-процессорами 2-го и 3-го столбцов рис. 5.7-б и имеет циклический по  вид:
вид: 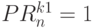 и
и 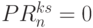 для всех
для всех  .
.
-
- 5.
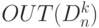 - выход вертикального канала транзита бит-процессоров 1-го столбца рис. 5.7-б:
- выход вертикального канала транзита бит-процессоров 1-го столбца рис. 5.7-б: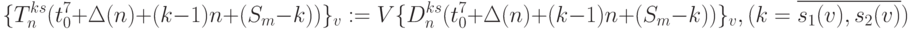
( 5.11)
В переменных и параметрах (5.1)-(5.5) и (5.7)-(5.11) отражен тот факт, что каждая  -я линейная последовательность слов-инструкций выполняется над всем потоком данных из
-я линейная последовательность слов-инструкций выполняется над всем потоком данных из  -битных слов, из кото-рых только одна реализует необходимую пользователю транспозицию
(
-битных слов, из кото-рых только одна реализует необходимую пользователю транспозицию
(  ). В результате объем работы, выполняемой
). В результате объем работы, выполняемой 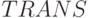 на каждом
на каждом  -м цикле, составляет
-м цикле, составляет 
 -разрядных слов-инструкций.
-разрядных слов-инструкций.
При использовании ЗУПВ объем работы минимален и составляет  разделенных во времени 2-цикловых слов-инструкций "чтения-записи", то есть
разделенных во времени 2-цикловых слов-инструкций "чтения-записи", то есть 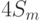 физически исполняемых слов-инструкций.
Такое более чем
физически исполняемых слов-инструкций.
Такое более чем  -кратное превышение фактически выполняемого объема работ над минимально необходимым обусловлено последовательным характером распространения потоков
-кратное превышение фактически выполняемого объема работ над минимально необходимым обусловлено последовательным характером распространения потоков 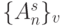 и
и  через линейные цепочки слов-инструкций, что является неотъемлемым атрибутом MIMD-бит-потоковой, а не ассоциативной организации вычислений.
через линейные цепочки слов-инструкций, что является неотъемлемым атрибутом MIMD-бит-потоковой, а не ассоциативной организации вычислений.
Как и в случае (5.1)-(5.5), из (5.7)-(5.11) невозможно определить вид выполняемой 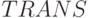 подстановки, который зависит не от переменных и параметров этих соотношений, а от содержимого потока
подстановки, который зависит не от переменных и параметров этих соотношений, а от содержимого потока 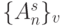 , которое и задает "момент времени"
, которое и задает "момент времени"  , когда в
, когда в  -й линейной цепочке выполняется условие
-й линейной цепочке выполняется условие 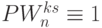 или
или 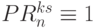 .
.
Структурно адаптируемый под параметры конкретной перестановки PD -ассоциативный порт вывода рис. 5.7-б позволяет:
- исключить слов-инструкции
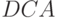 из (5.7)-(5.11), заменив их специфической для каждой подстановки
из (5.7)-(5.11), заменив их специфической для каждой подстановки 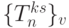 FIFO -регистровой схемы распространения сигнала "чтение" (
FIFO -регистровой схемы распространения сигнала "чтение" (  ) вида:
) вида:  первых бит - "единица", а остальные
первых бит - "единица", а остальные 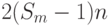 бит - "ноль";
бит - "ноль"; - в явном виде идентифицировать порядок чтения циклических FIFO -регистров, который определяется сдвигами во времени по отношению к входам схем "И" 1-го столбца рис. 5.7-б и который вычисляется согласно:
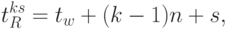
( 5.12) где
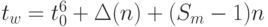 - начальная задержка на запись
- начальная задержка на запись  .
.
При значении переменных и параметров рис. 5.7 поток-инструкция 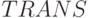 выполняет подстановку (5.6), что, согласно (5.12), дает:
выполняет подстановку (5.6), что, согласно (5.12), дает:  ;
; 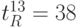 ;
;  ;
;  ;
; 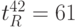 .
.
Для больших значений  синтез таких древообразных, FIFO -регистровых топологических схем под каждую подстановку (то есть по заданным
синтез таких древообразных, FIFO -регистровых топологических схем под каждую подстановку (то есть по заданным 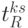 ) представляет достаточно сложную задачу, решение которой требует более чем
) представляет достаточно сложную задачу, решение которой требует более чем 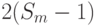 шагов.
шагов.
Особенности согласования параметров поток-инструкции 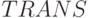 . В (5.1)-(5.5) и (5.7)-(5.11) считается, что
. В (5.1)-(5.5) и (5.7)-(5.11) считается, что 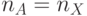 , то есть "глубина" адре-сации равняется количеству переставляемых данных
, то есть "глубина" адре-сации равняется количеству переставляемых данных 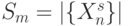 , а вид исполняемой подстановки может изменяться на каждом цикле выполнения поток-инструкции
, а вид исполняемой подстановки может изменяться на каждом цикле выполнения поток-инструкции 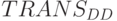 , то есть
, то есть 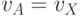 .
.
Однако на практике приходится решать задачи, в которых:
-
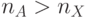 и все биты
и все биты 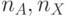 - значащие, что характерно для систем криптографической защиты видеоинформации, где "структура" исходного изображения наиболее эффективно разрушается при перестановке малоразрядных данных (
- значащие, что характерно для систем криптографической защиты видеоинформации, где "структура" исходного изображения наиболее эффективно разрушается при перестановке малоразрядных данных ( 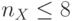 ) бит по всему изображению:
) бит по всему изображению: 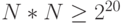 пикселей, а не по строкам или столбцам, то есть
пикселей, а не по строкам или столбцам, то есть 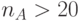 бит;
бит; -
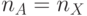 , но признак результата сравнения
, но признак результата сравнения 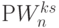 или
или 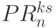 надо сформировать на время
надо сформировать на время 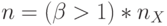 , что характерно для систем криптографической защиты речевой информации, где блочно-групповая
, что характерно для систем криптографической защиты речевой информации, где блочно-групповая 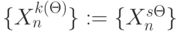 , а не пословная подстановка данных лучше разрушает "структуру" сообщения, то есть одному
, а не пословная подстановка данных лучше разрушает "структуру" сообщения, то есть одному 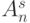 соответствует подмножество
соответствует подмножество 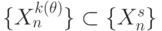 и
и 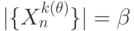 , а
, а 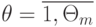 и
и 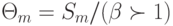 ;
; -
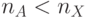 что характерно для систем криптографической защиты
телеметрической информации, где объектом подстановки являются блоки малоразрядных данных, измеряемых с разной частотой, что приводит к изменению состава блоков как внутри одной подстановки, так и на разных циклах ее выполнения, то есть
что характерно для систем криптографической защиты
телеметрической информации, где объектом подстановки являются блоки малоразрядных данных, измеряемых с разной частотой, что приводит к изменению состава блоков как внутри одной подстановки, так и на разных циклах ее выполнения, то есть 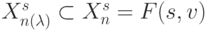 , и
, и 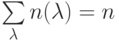
- цикл изменения вида подстановки больше цикла изменения преобразуемых данных:
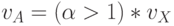 , что характерно для систем защиты слабо коррелированной информации, то есть
, что характерно для систем защиты слабо коррелированной информации, то есть 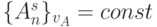 для всех
для всех 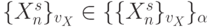
Все перечисленные ограничения создают определенные пробле-мы согласования темпов передачи и обработки потоков 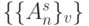 в слов-инструкциях
в слов-инструкциях  и потоков
и потоков 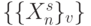 в слов-инструкциях
в слов-инструкциях 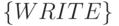 и
и  , которые при
, которые при 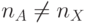 можно решить двумя способами:
можно решить двумя способами:
- Разбиением потока псевдослучайных адресов
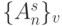 (при
(при  )
на "старшую" (
)
на "старшую" (  ) и "младшую" (
) и "младшую" (  ) половины таким образом, чтобы
) половины таким образом, чтобы 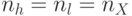 и
и 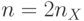 , из которых в
, из которых в 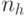 только
только 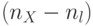 младших бит являются значащими, а остальные биты заполнены "нулями". В результате поток псевдослучайных адресов распадается на два составляющих потока
младших бит являются значащими, а остальные биты заполнены "нулями". В результате поток псевдослучайных адресов распадается на два составляющих потока 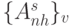 и
и 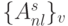 :
: 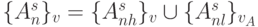 , которые обрабатыва-ются двумя параллельными поток-инструкциями
, которые обрабатыва-ются двумя параллельными поток-инструкциями 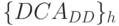 и
и  (соответственно четные и нечетные строки бит-матрицы рис. 5.8,где считается, что
(соответственно четные и нечетные строки бит-матрицы рис. 5.8,где считается, что 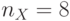 бит, а
бит, а 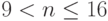 бит).
бит).Общий признак результата сравнения
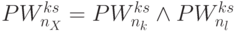 или
или 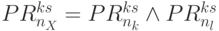 формируется бит-процессорами 8-го столбца бит-матрицы рис. 5.8, где на 1-й вход бит-инструкции
формируется бит-процессорами 8-го столбца бит-матрицы рис. 5.8, где на 1-й вход бит-инструкции 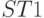 подается объединенный по "И" результат дешифрации в "четном" и "нечетном" терме. Двустрочные термы дешифрации выравнивают темпы обработки потоков преобразуемых данных
подается объединенный по "И" результат дешифрации в "четном" и "нечетном" терме. Двустрочные термы дешифрации выравнивают темпы обработки потоков преобразуемых данных 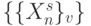 и адресов
и адресов 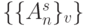 , но удваивают аппаратные затраты на дешифрацию. При этом в (5.1)- (5.5) и (5.7)-(5.11) надо использовать не
, но удваивают аппаратные затраты на дешифрацию. При этом в (5.1)- (5.5) и (5.7)-(5.11) надо использовать не  , а
, а 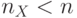 .
. - Прореживанием нулями потока псевдослучайных адресов
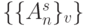 по правилу:
по правилу:- при
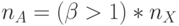 - в каждом псевдослучайном адресе
- в каждом псевдослучайном адресе 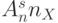 младших бит - значащие и
младших бит - значащие и 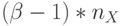 старших бит - нулевые,а в (5.1)-(5.5) и (5.7)-(5.11) надо использовать
старших бит - нулевые,а в (5.1)-(5.5) и (5.7)-(5.11) надо использовать 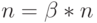 ; при этом функциональная задержка в каждой слов-инструкции
; при этом функциональная задержка в каждой слов-инструкции 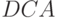 составляет не
составляет не 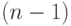 , а
, а 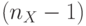 тактов;
тактов; - при
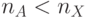 и
и 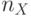 не кратно
не кратно 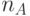 - в каждом псевдослучайном адресе
- в каждом псевдослучайном адресе 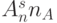 младших бит - значащие, а
младших бит - значащие, а 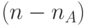 старших бит - нулевые, где
старших бит - нулевые, где 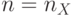
- при