Вспомогательные механизмы

Первым мы рассмотрим случай, когда область адреса назначения Обл(D) — не больше ,^{5 То есть меньшей или равной величины.} чем области обоих адресов источника, Обл(SA) и Обл(SB): Обл(D) Обл(SA) Обл(SB) или Обл(D) Обл(SB) Обл(SA). Тогда шансы на успех передачи при любом выборе довольно велики. В этом случае имеет смысл выбрать адрес источника, область которого поменьше, а значит поближе к области адреса назначения. Благодаря этому, скажем, диалог с удаленным внутриканальным адресом будет вестись с локального внутриканального адреса. Ведь политика безопасности удаленного хоста может быть более либеральной к внутриканальным адресам, чем к глобальным адресам.

Когда область адреса назначения Обл(D) — промежуточной величины: Обл(SA) Обл(D) Обл(SB) или Обл(SB) Обл(D) Обл(SA), — то шансы на успех больше у адреса источника большей величины. И наоборот, у адреса источника меньшей величины они явно недостаточны, потому что его область строго меньше, чем область адреса назначения. (Случай, когда они равновелики, мы уже включили в предыдущий вариант.)

Наконец, возможна ситуация, когда у адреса назначения область строго больше, чем у потенциальных адресов источника: Обл(SA) Обл(SB) Обл(D) или Обл(SB) Обл(SA) Обл(D). Но даже в этом случае еще не все потеряно. Ведь может оказаться, что интерфейс назначения находится в зоне адреса источника, например, глобальный адрес назначения находится "на канале" (§5.2). Чтобы повысить вероятность благоприятного исхода, надо выбрать адрес источника, область которого больше , а значит, потенциально охватывает больше интерфейсов. Это лучшее, что может сделать источник пакета в таких условиях.

Чтобы лучше почувствовать эти правила, давайте изобразим их графически, отложив по одной оси область SA, а по другой — область SB, как показано на рис. 9.2. Тогда все пространство задачи можно разбить на четыре участка согласно нашим правилам выбора лучшего адреса источника. В двух из них выбор уже предопределен, а еще в двух зависит от отношения величин областей SA и SB между собой.

Рис. 9.2. Выбор адреса источника по его области — начальная схема

Если через начало координат этого графика провести прямую с угловым коэффициентом 1 (см. рис. 9.3), то она разобьет все пространство задачи на две половины так, что в верхней область SA будет меньше, чем область SB, а в нижней — наоборот. Фактически, эта прямая может провести для нас выбор лучшего адреса там, где он все еще условный. Поэтому мы можем пересмотреть нашу графическую схему так, что на каждом участке сразу указан окончательный выбор адреса источника.

Рис. 9.3. Выбор адреса источника по его области — промежуточная схема

На первый взгляд у нас получилось шесть разных участков. Однако, присмотревшись внимательнее, мы заметим, что их можно свести к четырем (см. рис. 9.4), поскольку у двух участков SA есть общая граница, и то же самое справедливо для двух участков SB.

Рис. 9.4. Выбор адреса источника по его области — окончательная схема

А уже руководствуясь последней схемой, нетрудно записать оптимальный алгоритм выбора [§5 RFC 6724]:

Если Обл(SA) Обл(SB) то:

Если Обл(SA) Обл(D) то:

Предпочесть SB.

Иначе:

Предпочесть SA.

Иначе Если Обл(SA) 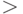Обл(SB) то:

Если Обл(SB) Обл(D) то:

Предпочесть SA.

Иначе:

Предпочесть SB.

Иначе:

Области SA и SB равны - ответ не определен.