НОУ ИНТУИТ | Параллельные вычисления и многопоточное программирование. Лекция 2: Параллельные вычисления

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 23.04.2013 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 27 студентам

| Поделиться |

Поддержать программу

Модель параллельного выполнения программы

Мы говорили об архитектуре вычислительных комплексов, способных обеспечить параллельное выполнение программ. Но архитектура комплекса - это лишь одно из требований, необходимых для реализации подлинного параллелизма. Другие два требования связаны с требованиями к операционной системе и к самой программе. Не всякую программу можно распараллелить независимо о того, на каком суперкомпьютерном комплексе она будет выполняться. В следующих главах мы подробнее поговорим о средствах операционной системы, обеспечивающих параллелизм вычислений, и о параллельных алгоритмах. Сейчас же рассмотрим некоторую модель параллельного выполнения, где главным действующим лицом будет программа.

Параллельные вычисления становятся одним из магистральных направлений развития информационных технологий. Можно указать на две причины, определяющие важность этого направления. Первая состоит в том, что стратегически важные для развития государства задачи могут быть решены только с применением суперкомпьютеров, обладающих сотнями тысяч процессоров, которые нужно заставить работать одновременно. Вторая причина связана с другим полюсом компьютерной техники, на котором находятся обычные компьютеры, ориентированные на массового пользователя. И эта техника становится многоядерной, и ее требуется эффективно использовать, так что параллельные вычисления требуются и здесь.

Для поддержки параллельных вычислений сделано достаточно много, начиная от архитектуры вычислительных систем, операционных систем, языков программирования до разработки специальных параллельных алгоритмов. Тем не менее, для программиста, решающего сложную задачу, построение и отладка эффективной параллельной программы все еще остается не простым занятием.

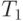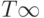Рассмотрим одну из моделей параллельного вычисления. Для этой модели мы хотим получить оценки времени выполнения программы одним процессором - T_1 , конечным числом процессоров - Т_p , и для идеализированного случая, когда число процессоров не ограничивается - $T \mathcal {1}$ .

Рассмотрим программу P, состоящую из n модулей:

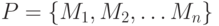
$P = \{M_1, M_2, …M_n\}$

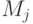Будем предполагать, что программа P выполняется на компьютере, обладающим некоторым числом процессоров, работающих на общей памяти. Выходные данные, полученные в результате работы модуля M_i , могут являться входными данными для модуля M_j . Так естественным образом возникает зависимость между модулями, определяющая возможный порядок их выполнения.

Множество модулей разобьём на k уровней. К уровню i отнесем те модули, для начала работы которых требуется завершение работы модулей верхних уровней, из которых хотя бы один принадлежит уровню i - 1. Модуль уровня i с номером k будем обозначать как 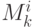M_k^i .

Модули, принадлежащие уровню 1, имеют все необходимые данные, полученные от внешних источников. Они не требуют завершения работы других модулей и в принципе могут выполняться параллельно, будучи запущенными в начальный момент выполнения программы.

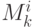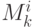Свяжем с программой P ориентированный граф зависимостей модулей. Граф не содержит циклов и отражает разбиение модулей на уровни. Модули являются вершинами графа, а дуги отражают зависимости между модулями. Дуга ведет от модуля M_k^i к модулю M_1^j , если для начала выполнения модуля M_k^i требуется завершение работы модуля M_1^j . В узлах графа содержится информация об ожидаемом времени выполнения модуля, где время измеряется в некоторых условных единицах. На Рис. 1.1 показан пример графа зависимостей:

Рис. 1.1. Пример графа зависимостей

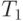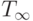Обозначим через T_1 - время, требуемое для выполнения программы P одним процессором, T_p - p процессорами, $T_{\mathcal {1}}$ - время, требуемое в случае, когда число процессоров неограниченно. В последнем случае достаточно n процессоров, по числу модулей нашей программы.

Предполагается, что все эти характеристики рассчитываются при соблюдении двух условий:

Выполняются зависимости между модулями, заданные графом зависимостей.
Характеристики вычислены для оптимального расписания работы процессоров.

В случае одного процессора достаточно выполнение только первого условия. Обычно предполагается естественный порядок выполнения модулей, - последовательное выполнение модулей одного уровня, затем переход к выполнению модулей следующего уровня.

Для случая неограниченного числа процессоров оптимальным является такое расписание, когда каждый модуль начинает выполняться, как только завершены все модули, необходимые для его работы.

Для случая p процессоров можно распределить модули по процессорам, задав для каждого процессора P_i множество модулей, выполняемых этим процессором:

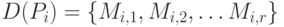
$D(P_i)=\{M_{i,1},M_{i,2},… M_{i,r}\}$

Распределение модулей по процессорам совместно с графом зависимостей однозначно определяет расписание работ и время выполнения программы при данном расписании. Предполагается, что каждый процессор выполняет модули из распределения D(P_i) . После завершения очередного модуля он сразу же переходит к выполнению следующего модуля, если для этого модуля выполнены все зависимости, заданные графом зависимостей. В противном случае процессор ждет окончания работы требуемых модулей. Время завершения последнего модуля в распределении D(P_i) задает время работы данного процессора. 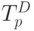Тот процессор, который последним заканчивает работу и определяет общее время решения задачи T_p^D для данного расписания. Введенная ранее характеристика T_p предполагает оптимальное расписание:

Задача составления оптимального расписания относится к сложным задачам. На практике для программ большого размера не удается явно вычислить значение T_p . По этой причине несомненный интерес представляет получение оценок для T_p .

Для введенных характеристик выполняется естественное соотношение:

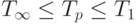$T_{\mathcal {1}}\le T_p\le T_1$

( 1.1)

Нас будет интересовать получение более точных оценок для T_p .

Рассмотрим вначале упрощенную ситуацию, предположив, что время выполнения всех модулей одинаково и равно t. Нетрудно видеть, что

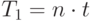$T_1=n\cdot t$

( 1.2)

Действительно, один процессор должен выполнить все модули программы, проходя, например, последовательно один уровень за другим.

Нетрудно посчитать и время 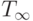$T_{\mathcal {1}}$

$T_{\mathcal {1}}=k\cdot t$

( 1.3)

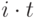Действительно, пусть на первом уровне n_1 модулей. У них есть все необходимые данные, и они могут выполняться параллельно. Поскольку число процессоров неограниченно, то запустив каждый модуль на одном из n_1 имеющихся процессоров, за время t завершим выполнение модулей первого уровня. Пусть за время $i \cdot t$ завершено выполнение всех модулей всех уровней от первого до i-го. Тогда возможно параллельно выполнять модули следующего i + 1-го уровня, число которых равно 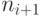$n_{i+1}$ . Процессоров у нас хватает, поэтому на завершение всех модулей этого уровня потребуется t времени, и общее время выполнения равно $(i + 1) \cdot t$ , что по индукции доказывает справедливость формулы (3).

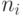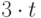Для времени T_p получим оценки сверху и снизу. Понятно, что p процессоров, начав одновременно работать, могут выполнить вычисление n_i модулей уровня i за время $\left \lceil \frac{n_i}{p}\right \rceil \cdot t$ , где $\left \lceil x\right \rceil$ обозначает минимальное целое, большее или равное x. Два процессора смогут выполнить пять модулей уровня 1 за время $3 \cdot t$ . Отсюда следует, что общее время работы T_p дается формулой:

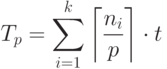$T_p=\sum_{i=1}^k \left \lceil \frac{n_i}{p}\right \rceil \cdot t$

( 1.4)

Поскольку $\left \lceil x\right \rceil \ge x$ , то

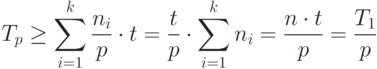$T_p\ge \sum_{i=1}^k \frac{n_i}{p} \cdot t=\frac{t}{p}\cdot \sum_{i=1}^k n_i=\frac{n \cdot t}{p}=\frac{T_1}{p}$

( 1.5)

Формула (5) дает нижнюю оценку времени выполнения работы p процессорами.

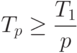$T_p \ge \frac{T_1}{p}$

( 1.6)

Если на каждом уровне число модулей 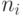n_i кратно p, то оценка достижима. В лучшем случае p процессоров могут сократить время выполнения программы в p раз в сравнении со временем, требуемом для выполнения этой работы одним процессором.

Получим теперь оценку сверху. Поскольку 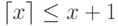$\left \lceil x\right \rceil \le x+1$ , то

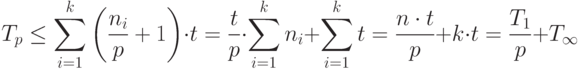$T_p\le \sum_{i=1}^k \left ( \frac{n_i}{p}+1\right) \cdot t=\frac{t}{p}\cdot \sum_{i=1}^k n_i+\sum_{i=1}^k t=\frac{n \cdot t}{p}+k \cdot t=\frac{T_1}{p}+T_{\mathcal {1}}$

( 1.7)

Объединяя (6) и (7), получим

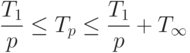$\frac{T_1}{p}\le T_p\le \frac{T_1}{p}+T_{\mathcal {1}}$

( 1.8)

Оценки (8) для случая, когда время выполнения всех модулей одинаково, известны [5].

Рассмотрим теперь более интересный для практики случай, когда модули программы для своего выполнения требуют разного времени. Пусть 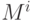M^i - множество модулей уровня i:

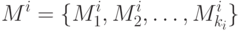$M^i=\{M^i_1, M^i_2, …, M^i_{k_{i}}\}$

( 1.9)

Для каждого из этих модулей известно время, требуемое на его выполнение - 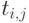$t_{i, j}$ .

И в этом случае нетрудно рассчитать время 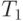T_1 - время, требуемое на выполнение всей работы одним процессором:

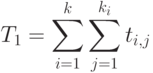$T_1= \sum_{i=1}^k \sum_{j=1}^{k_i} t_{i, j}$

( 1.10)

Как рассчитать время 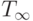$T_{\mathcal {1}}$ в этой ситуации, когда мы располагаем неограниченным числом процессоров? Введем для каждого модуля время окончания его работы - 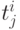t_j^i . Это время будем рассчитывать по следующей формуле:

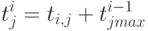$t_j^i= t_{i, j}+t_{jmax}^{i-1}$

( 1.11)

Здесь $t_{jmax}^{i-1}$ - время окончания работы того модуля уровня i-1, который:

необходим для работы модуля ;
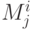из всех необходимых модулей завершает свою работу последним.

Тогда время 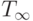$T_{\mathcal {1}}$ можно рассчитать следующим образом:

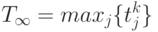$T_{\mathcal {1}}= max_j \{ t_j^k \}$

( 1.12)

Формула (12) говорит, что время завершения последнего модуля уровня k и является временем 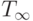$T_{\mathcal {1}}$ при оптимальном расписании работ. Справедлива следующая теорема:

Дальше >>

Параллельные вычисления и многопоточное программирование

Параллельные вычисления и многопоточное программирование

Параллельные вычисления

Модель параллельного выполнения программы

Вопросы и ответы

Студенты

Авторизоваться

Параллельные вычисления и многопоточное программирование

Параллельные вычисления и многопоточное программирование

Параллельные вычисления

Модель параллельного выполнения программы

Вопросы и ответы

Студенты