НОУ ИНТУИТ | Инструктивный синтез нанометровых вычислительных структур. От задач к вычислительным моделям и структурам . Лекция 4: Теория вычислений и машины Тьюринга

Учитесь и получайте официальные документы БЕСПЛАТНО. Вы можете поддержать наш проект.

Регистрация Вход

Твой путь к знаниям!

Опубликован: 03.04.2013 | Уровень: для всех | Доступ: платный

|

Вам нравится? Нравится 21 студенту

| Поделиться |

Поддержать программу

3.2. Машины Тьюринга и вычислимые функции

Приведенных в предыдущем разделе данных достаточно для перехода к общему описанию 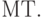МТ.

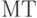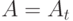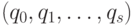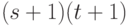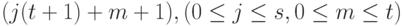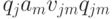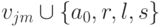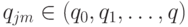Работу с рабочим алфавитом $A =A_{t}$ и состояниями $(q _{0}, q _{1}, …, q_{s})$ можно представить таблицей машины , которая представляет собой матрицу с 4 столбцами и (s+1)(t+1) строками. Строка матрицы с номером $(j(t+1)+m+1), (0 \le j \le s, 0\le m \le t)$ имеет вид: $q_{j} a_m v_{jm} q_{jm}$ , где действие $v_ {jm}\inA\cup\{ a _{0}, r , l , s \}$ , а $q_{jm} \in ( q _{0}, q _{1}, …, q)$ - следующее состояние. 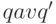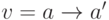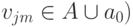Индексы элементов строки матрицы в ряде случаев можно опускать, и тогда описание строки принимает вид qavq' , где действие может представлять собой подстановку символа (qaa' q' вида $v = a \to a'$ , при этом $v_{jm} \in A\cup{a _{0}})$ , сдвиг вправо на одну ячейку $(qarq' \text{ вида } v = r)$ , сдвиг влево на одну ячейку, если рабочая ячейка не совпадает с нулевой $(qalq' \text{ вида } v = l )$ . 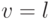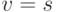Если рабочая ячейка совпадает с нулевой и v = l , то требуемое действие невыполнимо и останавливается v = s , что вызвано ее выходом за пределы ленты. Машинный останов 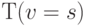Т (v = s) может быть и запланированным. Считается также, что пара 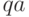однозначно идентифицирует единственную строку матрицы . В нашем примере матрица 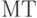имеет вид:

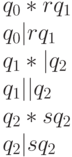
$q _{0} * r q_{1} \\ q_{0} | r q_1 \\ q _{1} * | q _{2 } \\ q _{1} | | q _{2 } \\ q_{2} * s q_{2 } \\ q _{2} | s q_2$

Строки таблицы с одинаковыми соответствуют некоторому указанию в смысле требования 1, и наоборот, состояниям отвечают номера указаний в соответствующем алгоритмическом предписании.

Таблицу 3.1,задающую правила подстановки символов при арифметическом сложении, также можно представить в виде таблицы машины Тьюринга (табл. 3.2), если пару 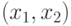$(x _{1}, x _{2})$ считать одним символом, а $q_1: = e^{+}= 0$ , и $q_{2}:= e^{+}= 1$ .

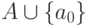В принятых соглашениях запись на ленте или просто запись является функцией на со значениями в $A\cup\{a _{0}\}$ , которая каждому ставит в соответствие букву, являющуюся содержимым -й ячейки ленты. При этом неравенство $Y(i) \ne *$ выполняется только для конечного числа индексов .

Согласно требованию 1 общий итог выполненных вычислений однозначно определяется конфигурацией 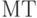, которая задается тройкой 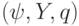$(\psi , Y, q)$ , где $\psi$ - номер текущей рабочей ячейки, - текущая запись и - текущее состояние . Конфигурации обычно обозначают , …, а начальной конфигурации отвечает та, у которой третья компонента есть $q _{0}$ .

Таблица 3.2. Таблица преобразования символов при сложении по "Тьюрингу"
$(x_1, х_{2})$	$\Sigma$		$(x_1, х_{2})$	$\Sigma$	$q_{jm}$	$(x_1, х_{2})$	$\Sigma$
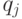
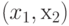
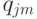
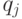
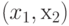
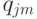
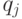
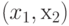
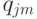
0,0	0	.	.	.	.	3,3	6
0,1	1		1,9	1		3,4	7
			2,2	4
0,9	9		2,3	5		3,9	2
0,0	1
0,1	2		2,5	7		3,3	7
						3,4	8
0,9	0		2,9	1
1,1	2		2,2	5		3,9	3
1,2	3		2,3	6
			2,4	7
1,9	0		2,5	8		7,7	4
1,1	3					7,8	5
1,2	4		2,9	2

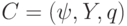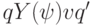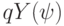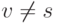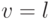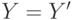Пусть $C = ( \psi , Y, q)$ - некоторая конфигурация . Если $qY(\psi)vq'$ есть некоторая строка таблицы , начинающаяся символами $qY(\psi)$ , и если $v \ne s$ и одновременно не выполняются равенства v = l и $\psi = 0$ , то выполнение действия приводит к новой рабочей ячейке с номером $\psi$ (при этом не исключается $\psi = \psi'$ ) и к новой записи (при этом не исключается Y = Y' ) и переходит в состояние q ' . 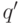В этом случае однозначно определенную конфигурацию 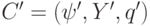$C' = ( \psi' , Y', q')$ называют следующей за 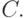В противном случае ( 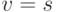v = s или одновременно 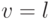v = l и $\psi = 0$ ) говорят, что является конечной конфигурацией для .

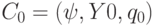Говорят, что применима к записи в рабочей ячейке $\psi$ , если в качестве начальной конфигурации выбрана конфигурация $C _{0} = ( \psi , Y0, q_{0})$ .

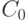Конфигурация $C _{0}$ однозначным образом порождает конечную или бес-конечную последовательность конфигураций 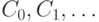$C _{0}, C _{1}, …$ , в которой 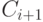$C_{i+1}$ есть конфигурация, следующая за $C_{i}$ , и для которой $C_{i}$ есть последний член в том и только в том случае, когда $C_{i}$ является конечной конфигурацией. Так как 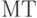работает в пошаговом режиме, между номером шага и номером конфигурации существует взаимно однозначное соответствие. 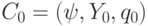Поэтому машина останавливается через конечное число шагов после применения к записи в рабочей ячейке $\psi$ , если последовательность конфигураций, порожденная $C _{0} = (\psi , Y_0, q _{0})$ , имеет последний член. 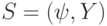Если для анализа вычислений после-довательность состояний не представляет интереса, то сам вычислительный процесс можно описать двойками $S = (\psi , Y)$ , которые каждой конфигурации 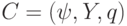$C = ( \psi, Y, q)$ сопоставляют ее позицию, то есть последовательности конфигураций всегда соответствует последовательность позиций, к которым применимы термины "начальная" и "конечная".

Пусть 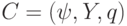$C = ( \psi, Y, q)$ есть некоторая конфигурация и 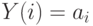Y(i) = a_i для всех 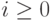$i \ge 0$ . Тогда для наглядного изображения и отвечающей ей позиции можно использовать:

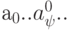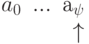
$а_{0}..a_{\psi}^0 ..$ . и $\begin{array}{rrr} a_0&...& а_{\psi} \\ &&\uparrow \end{array}$

Безразличные для анализа участки записи будем обозначать символом 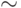$\sim$ , а если речь идет о содержимом одной ячейки, то символом $\clubsuit.$ Это позволяет для записи позиций использовать следующие упрощения.

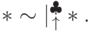
Выделить только интересующие позиции типа: $*\sim | \substack{\clubsuit\\\uparrow}*.$
Обозначить специальным символом 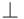$\bot$ значимый левый (правый) край ленты типа: $\bot ** \substack{|\\\uparrow}*\bot$
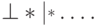
Исключить повторяющийся символ правее определенного: $\bot*|\substack{*\\\uparow}\ldots.$

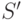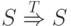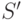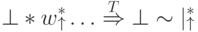Пусть и возможные позиции для . Тогда запись вида $S\stackrel{T}{\Rightarrow}S$ означает: начала свою работу в начальной позиции и (после конечного числа шагов) остановилась в конечной позиции . Например: $\bot*w\substack{*\\\uparrow}\ldots\stackrel{T}{\Rightarrow}\bot\sim|\substack{*\\\uparrow}$ .

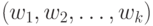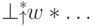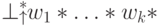Применить к записи после слова или после -членной последовательности слов $(w_1, w_{2}, …, w_k )$ над означает взять в качестве начальной позицию: $\bot\substack{*\\\uparrow}w*\ldots$ , и соответственно $\bot\substack{*\\\uparrow}w_1*\ldots* w_k*$ .

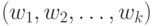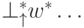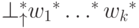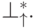
Применить к записи перед словом или перед -членной последовательностью слов $(w_1, w_{2}, …, w_k)$ над означает взять в качестве начальной позицию: $\bot^*_{\uparrow} w^*\ldots$ , и соответственно $\bot^*_{\uparrow} {w_1}^*\ldots^*{w_k}^*$ . Применить к пустой ленте означает взять в качестве начальной позицию $\bot^*_{\uparrow}.$

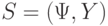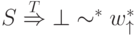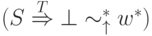Говорят, что остановилась после (перед) словом , если применялась к начальной записи в начальной ячейке $S = (\Psi , Y)$ и $S \stackrel{T}{\Rightarrow}\bot\sim^*w^*_{\uparrow}$ , $(S \stackrel{T}{\Rightarrow}\bot\sim^*_{\uparrow}w^*)$ . При этом в конечной позиции после символа нельзя сказать ничего определенного.

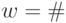Если в результате применения к записи в рабочей ячейке $\Psi$ остановилась после слова над , то последняя рабочая ячейка не может быть нулевой, даже если $w = \#$ , так как фактически произошел машинный останов .

Для строгого определения вычислимых по Тьюрингу функций используется экстенсиональная точка зрения, которая исходит из следующего:

Две функции равны, если совпадают их области определения и если их значения во всех общих точках определения равны.
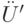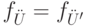Два алгоритма $\ddot{U}$ и $\ddot{U}'$ экстенсионально равны (равны по конечному эффекту), если равны вычисляемые ими функции $f_{\ddot{U}} = f_{\ddot{U}'}$ .

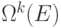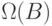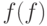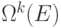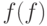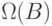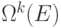Функцию называют функцией из $\Omega^{k}(E)$ в $\Omega (B)$ , если область определения $f (\Def{f})$ содержится в $\Omega^{k}(E)$ , а множество образов при ото-бражении $f (\Bild{f} )$ , содержится в $\Omega(B)$ . В предельном случае $\Def {f} = \Omega^{k}(E)$ , и тогда называют функцией на $\Omega^{k}(E)$ со значениями в 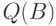Q(B) . 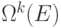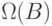В общем случае $\Def{ f}\subset \Omega^{k}(E)$ , и тогда называют частичной функцией на $\Omega^{k}(E)$ со значениями в $\Omega(B)$ .

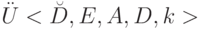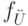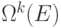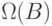Алгоритм $\ddot{U}< \breve{D} , E, A, D, k>$ определяет функцию $f_{\ddot{U}}$ из $\Omega^{k}(E)$ в $\Omega(B)$ , если выполнены следующие условия:

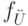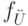Функция $f_{\ddot{U}}$ определена для $w\in\Omega^k(E)$ в том и только в том случае, когда применение $\ddot{U}$ к приводит к некоторому результату, который и является значением $f_{\ddot{U}}$ от .
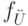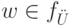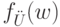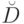Функция $f_{\ddot{U}}$ обладает тем свойством, что для всех $w\in\Def{ f_{\ddot{U}}}$ значение $f_{\ddot{U}}(w)$ можно вычислить, исполнив предписание $\breve{D}$ .

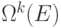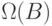Отсюда, функция из $\Omega^{k}(E)$ в $\Omega (B)$ называется вычислимой тогда и только тогда, когда существует алгоритм 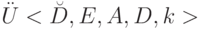$\ddot{U}<\breve{D} , E, A, D, k>$ , для которого 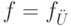$f = f_{\ddot{U}}$ . В этом случае $\ddot{U}$ называют вычислительной процедурой для .

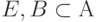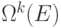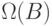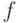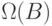В терминах МТ те же определения имеют следующий вид. Пусть есть МТ с рабочим алфавитом , таким, что $E, B \subset А$ . Тогда определяет некоторую -местную функцию $(k \ge 0)$ из $\Omega^{k}(E)$ в $\Omega (B)$ по следующему правилу: $w\in\Omega^{k}(E)$ принадлежит области $\Def{f}$ тогда и только тогда, когда , примененная к записи , останавливается после слова из $\Omega (B)$ , а это слово является значением от .

Таким образом, для 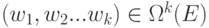$(w_1,w_2... w_k)\in\Omega^{k}(E)$ имеем:

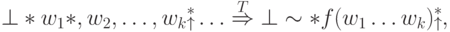
$\bot * w_{1}*, w_{2}, \ldots, w_{k}\substack{*\\\uparrow}\ldots\stackrel{T}{\Rightarrow} \bot\sim *f(w_1\ldots w_k) \substack{*\\\uparrow},$

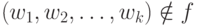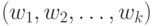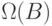когда $(w_1…w_k )\in\Def{ f}$ , и наоборот, если $(w_1, w_{2}, …, w_k )\notin\Def{ f}$ , то , примененная к записи $(w_1, w_{2}, …, w_k)$ , не останавливается после слова из $\Omega (B)$ .

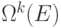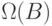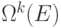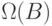Приведенных данных достаточно для определения 3.1: функция из $\Omega^{k}(E)$ в $\Omega (B)$ называется вычислимой по Тьюрингу ( ФВТ ), если существует МТ с рабочим алфавитом , содержащим и , такая, что -местная функция из $\Omega^{k}(E)$ в $\Omega (B)$ , определяемая машиной , совпадает с .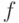

О любой такой МТ говорят, что она вычисляет .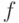

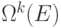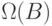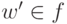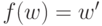Из приведенного определения следует, если есть ФВТ из $\Omega^{k}(E)$ в $\Omega (B)$ и есть МТ, вычисляющая , то, применив к $w\in\Omega^{k}(E)$ , можно получить следующие результаты: либо не остановится вовсе, либо уйдет за пределы ленты, либо произойдет машинный останов . Если в последнем случае остановилась после слова $w'\in\Omega(B)$ , то $w'\in\Def{f}$ и f(w) = w' . Во всех остальных случаях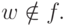 $w\notin\Def{f}.$

Введенное описание применения к аргументу ФВТ, вычисляемой , и нахождение значения функции способом, указанным в определении 3.1, вместе образуют общее предписание для всех алгоритмов. Это позволяет говорить, что функция, вычислимая по Тьюрингу ( ФВТ ), является адекватной формализацией интуитивного понятия "вычислимая функция".

Дальше >>

Введение в отказоустойчивые технологии высокопроизводительных вычислительных систем (суб)микронного, супрамолекулярного и нанометрового диапазона

Инструктивный синтез нанометровых вычислительных структур. От задач к вычислительным моделям и структурам

Теория вычислений и машины Тьюринга

3.2. Машины Тьюринга и вычислимые функции

Вопросы и ответы

Студенты

$(x_1, х_{2})$	$\Sigma$		$(x_1, х_{2})$	$\Sigma$	$q_{jm}$	$(x_1, х_{2})$	$\Sigma$
0,0	0	.	.	.	.	3,3	6
0,1	1		1,9	1		3,4	7
			2,2	4
0,9	9		2,3	5		3,9	2
0,0	1
0,1	2		2,5	7		3,3	7
						3,4	8
0,9	0		2,9	1
1,1	2		2,2	5		3,9	3
1,2	3		2,3	6
			2,4	7
1,9	0		2,5	8		7,7	4
1,1	3					7,8	5
1,2	4		2,9	2

$(x_1, х_{2})$	$\Sigma$		$(x_1, х_{2})$	$\Sigma$	$q_{jm}$	$(x_1, х_{2})$	$\Sigma$
0,0	0	.	.	.	.	3,3	6
0,1	1		1,9	1		3,4	7
			2,2	4
0,9	9		2,3	5		3,9	2
0,0	1
0,1	2		2,5	7		3,3	7
						3,4	8
0,9	0		2,9	1
1,1	2		2,2	5		3,9	3
1,2	3		2,3	6
			2,4	7
1,9	0		2,5	8		7,7	4
1,1	3					7,8	5
1,2	4		2,9	2

Авторизоваться

Введение в отказоустойчивые технологии высокопроизводительных вычислительных систем (суб)микронного, супрамолекулярного и нанометрового диапазона

Инструктивный синтез нанометровых вычислительных структур. От задач к вычислительным моделям и структурам

Теория вычислений и машины Тьюринга

3.2. Машины Тьюринга и вычислимые функции

Вопросы и ответы

Студенты

$(x_1, х_{2})$	$\Sigma$		$(x_1, х_{2})$	$\Sigma$	$q_{jm}$	$(x_1, х_{2})$	$\Sigma$
0,0	0	.	.	.	.	3,3	6
0,1	1		1,9	1		3,4	7
			2,2	4
0,9	9		2,3	5		3,9	2
0,0	1
0,1	2		2,5	7		3,3	7
						3,4	8
0,9	0		2,9	1
1,1	2		2,2	5		3,9	3
1,2	3		2,3	6
			2,4	7
1,9	0		2,5	8		7,7	4
1,1	3					7,8	5
1,2	4		2,9	2