| Россия |
Программирование, основанное на правилах преобразований
10.1.2. Локальные правила преобразования
Зачастую преобразование требуется осуществить не во всём тексте программы, а в отдельно взятом выражении или группе выражений. В этом случае прибегают к локальным правилам преобразования. С локальными правилами преобразования мы уже встречались в предыдущих лекциях, в частности, при работе с дифференциальными уравнениями, при выполнении символьных вычислений. В настоящей лекции мы познакомимся с ними как с основой соответствующего стиля программирования.
Локальными вариантами функций немедленного присваивания Set и отложенного присваивания SetDelayed являются функции Rule и RuleDelyed. Их инфиксные формы выглядят как " -> " и " :> ", соответственно. Ещё две инфиксные формы задания этих функций выглядят соответственно как " \to " и " :\to ", и ввести их можно, пользуясь палитрой. Кроме того, в последних версиях Mathematica введённое с клавиатуры выражение -> автоматически преобразовывается в " \to ", а " :> " — в " :\to ". С функцией Rule в инфиксной форме мы уже имели дело, когда в предыдущих лекциях знакомились с опциями функций.
Как мы уже знаем, если в тексте программы мы воспользуемся функцией Set[x,y], то во всех выражениях, содержащих символ x, он будет заменён символом y. Если же в тексте программы мы воспользуемся функций Rule[x,y] (пример In[1] на рис. 10.6), то никаких замен, связанных с символом x, ни в одном выражении не произойдёт (пример In[2]). Для того чтобы всё-таки осуществить замену в некотором выражении, нужно воспользоваться функцией ReplaceAll, указав в качестве её аргументов это самое выражение и необходимую локальную замену. Если, например, в выражении x^2+x+1 мы хотим заменить символ x выражением a+b, то мы задаём соответствующую функцию в следующей форме: ReplaceAll[x^2+x+1,Rule[x,a+b]] (пример In[3]). Функция ReplaceAll также имеет инфиксное представление, которое задаётся как " /. ". Итак, функцию из предыдущего примера можно задать следующим образом:  (пример In[4]).
(пример In[4]).
Выражения, содержащие локальные правила преобразования, также имеют собственный порядок вычислений, описанный П. Веллином и др. в [14, с. 165]. В случае немедленной замены при использовании функции Rule порядок вычислений следующий. Сначала полностью вычисляется выражение, выступающее в качестве первого аргумента функции ReplaceAll (или находящееся слева от инфиксного выражение " /. "). Затем вычисляются выражения в левой и правой частях правил преобразования (второго аргумента функции ReplaceAll или стоящего справа от " /. "). В самом конце выражения в левой части правил, содержащиеся в первом аргументе функции ReplaceAll, заменяются выражениями в правой части правил. Порядок расчёта можно проследить при помощи уже известной нам функции Trace.
В примере In[1] на рис. 10.7 мы задаём некоторое выражение  , представляем его в полиномиальном виде, и осуществляем замену символов m и n выражениями Sin[2.] и Cos[2.], соответственно. В том же примере мы знакомимся с тем фактом, что к одному и тому же выражению мы можем применять одновременно несколько правил преобразований: в этом случае они должны быть оформлены в виде списка. В примере In[2] мы применяем функцию Trace к выражению в In[1]. По результату, содержащемуся в Out[2], можно поэтапно проследить, что Mathematica делает с исходным выражением на каждом этапе:
, представляем его в полиномиальном виде, и осуществляем замену символов m и n выражениями Sin[2.] и Cos[2.], соответственно. В том же примере мы знакомимся с тем фактом, что к одному и тому же выражению мы можем применять одновременно несколько правил преобразований: в этом случае они должны быть оформлены в виде списка. В примере In[2] мы применяем функцию Trace к выражению в In[1]. По результату, содержащемуся в Out[2], можно поэтапно проследить, что Mathematica делает с исходным выражением на каждом этапе:
- вычисляет заданное выражение Expand[(m+n)^2] и получает в результате вычисления новое выражение
 ;
; - вычисляет значение выражения Sin[2.], получает число 0.909297;
- переписывает первое правило преобразования c учётом результатов предыдущего пункта как
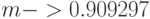 ;
; - вычисляет значение выражения Cos[2.], получает -0.416147;
- переписывает второе правило преобразования c учётом результатов предыдущего пункта как
 ;
; - переписывает все правила преобразований с учётом вычислений в виде {m->0.909297,n->-0.416147};
- полностью переписывает выражение с правилами преобразований с учётом всех проведённых вычислений, m^2+2mn+n^2/.{m->0.909297,n->-0.416147};
- производит замену в соответствии с правилами преобразований,
 ;
; - по отдельности вычисляет значения каждого члена выражения, полученного в предыдущем пункте;
- переписывает выражение, полученное в пункте 8 сего перечня с учётом вычислений в предыдущем пункте, 0.826822 -0.756802 +0.173178, проводит вычисления и получает конечный результат 0.243198 (который, к слову, совпадает с выражением в Out[1] на рис. 10.7).
В случае отложенной замены (функция RuleDelayed) вычисление выражений в правой части правил преобразований осуществляется после подстановки, то есть, пункты 2 и 4 представленного выше перечня следуют после пункта 7. Это также легко пронаблюдать при помощи функции Trace — см. пример In[4] на рис. 10.7.
Правила преобразования могут применяться к символам, причём нигде не оговорено, какую роль в тексте программы эти символы должны выполнять. В предыдущих примерах мы применяли замену к символам, являющимся переменными в некотором выражении. Однако преобразуемый символ может являться и заголовком выражения. В примере In[1] на рис. 10.8 мы преобразуем полином в список входящих в него слагаемых, заменяя символ Plus, задающий сумму выражений, символом List, задающим список. Обратный пример преобразования списка в сумму его элементов приведён в книге П. Веллина и др. [14, с. 166].
В примере 10.7 мы уже познакомились с возможностью применения к выражению одновременно нескольких правил преобразований: для этого правила оформляются в виде списка. Следует учесть, что эффект параллельного применения правил отличается от последовательного, когда каждое новое правило применяется при помощи отдельной функции ReplaceAll. В примере In[2] на рис. 10.8 мы одновременно применили к выражению  правила преобразования
правила преобразования  и
и  , а в примере In[3] — последовательно. Результаты вычислений Out[2] и Out[3] разительно отличаются друг от друга. Объясняется это достаточно просто: если в первом случае (в примере In[2]) оба правила, и a->x, и x->y, применяются к исходному выражению
, а в примере In[3] — последовательно. Результаты вычислений Out[2] и Out[3] разительно отличаются друг от друга. Объясняется это достаточно просто: если в первом случае (в примере In[2]) оба правила, и a->x, и x->y, применяются к исходному выражению  , то во втором (в примере In[3]) к нему применяется только правило
, то во втором (в примере In[3]) к нему применяется только правило  , а правило
, а правило  применяется к результату предыдущей замены, то есть, к уже изменённому выражению.
применяется к результату предыдущей замены, то есть, к уже изменённому выражению.
Зачастую в процессе вычисления некоторого выражения каждое новое преобразование, подразумевающее замену некоторого символа expr1 символом expr2, приводит к новому выражению, вновь содержащему expr1. Если задачей ставится окончательно избавиться от expr1 в исходном выражении, заменив его выражением expr2, можно прибегнуть к многократному применению правил преобразования. Функция ReplaceRepeated, заданная в виде ReplaceRepeated[initaxpr,rules], будет до тех пор применять правила rules, пока получаемое в результате выражение не перестанет изменяться. Инфиксная форма функции ReplaceRepeated в Mathematica — " //. ". В примере In[4] на рис. 10.8 мы воспользовались многократным преобразованием некоторого выражения, а в примере In[5] для сравнения применили однократное преобразование. Как мы видим, в результате вычислений Out[5] по-прежнему содержится символ q, для которого задавалось правило, а в Out[4] символов, требующих замены не осталось.
Однако следует быть осторожным при работе с функцией ReplaceRepeated: некоторые правила преобразования могут вызывать принципиальную невозможность точного выполнения функции. Так в примере In[6] на рис. 10.8 мы пытаемся заменить содержащийся в исходном выражении символ t выражением, которое также содержит этот символ, тем самым, ввергая программу в бесконечную рекурсию. В результате мы получаем сообщение о том, что операция преобразования была выполнена 65536 раз и после этого остановлена, а выходная ячейка Out[6] содержит результат применения правила преобразования 65536 раз.
Подробней о локальных правилах преобразований см. книги Е. М. Воробьёва [1, с. 141, 158–162] и П. Веллина и др. [14, с. 164–167].



