| Россия |
Работа со списками
3.7. Работа со строками
Строки по своей структуре очень напоминают списки: в качестве элементов в строках используются символы и цифры. Поэтому многие функции, предназначенные для работы со строками, очень похожи по функционалу и способу задания параметров на функции для списков.
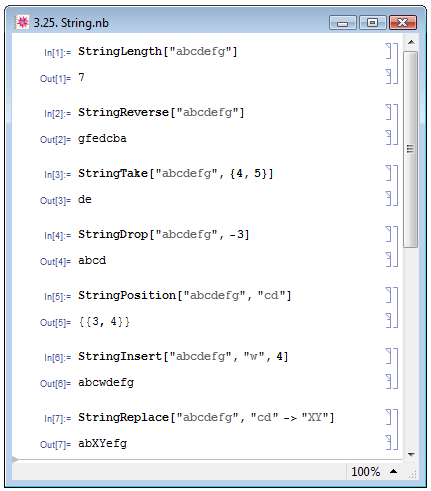
StringLength[str] возвращает длину (число символов) строки.
StringReverse[str] осуществляет запись символов строки в обратном порядке.
Функции Take[str,cond] и Drop[str,cond] позволяют обратиться к символам, имеющим заданные условиями cond номера, причём условия cond определяются так же, как и в соответствующих функциях для списков.
StringPosition[str,expr] показывает номер позиции выражений expr в строке str.
StringInsert[str,expr,n] добавляет выражение expr в строку str на позицию с номером n.
StringReplace[str,expr->expr2] заменяет в строке str выражение expr1 выражением expr2.
Примеры использования описанных выше функций см. на рис. 3.25.
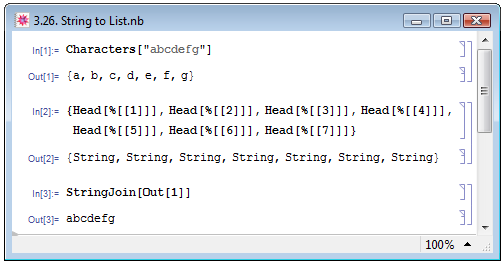
Функция Characters[str] позволяет конвертировать строку str в список. Однако элементами полученного списка будут не символы, содержащиеся в исходной строке, а строки, содержащие каждый символ в отдельности, т.е., функция Characters преобразует некоторую строку "abcdefg" в список {"a","b","c","d","e","f","g"} — см. примеры In[1] и In[2] на рис. 3.26.
Преобразовать список в строку позволяет функция StringJoin[list] — пример In[3] на рис. 3.26.
Подробней о работе со строками см. книгу П. Веллина и др. [14, с. 70–72].
Ключевые термины
Вложенный список — список, элементами которого являются другие списки.
Внутренний список — список, являющийся элементом вложенного списка.
Глубина вложенного списка — число уровней вложенного списка.
Длина списка — число элементов списка.
Итератор — объект, указывающий на расположенные определённым образом элементы в наборе данных.
Список — форма структурирования данных, по строению представляющая собой множество элементов, заключённых в фигурные скобки и разделённых запятыми.
Краткие итоги
В данной лекции мы подробно познакомились с третьим классом данных Mathematica — списками. Мы научились задавать списки, как вручную, так и пользуясь широким спектром предназначенных для этого встроенных функций Mathematica. Мы познакомились с такими сложными объектами, как вложенные списки, также принципами их задания и работы с ними. Мы научились выявлять структуру списков, извлекать информацию о количестве и характере их элементов, о количестве уровней вложенных списков. Мы познакомились с встроенными функциями Mathematica, позволяющими избирательно обращаться к требуемым элементам списков, модифицировать списки. Мы узнали, какой эффект оказывает на результат вычислений применение к спискам математических функций. Мы более подробно познакомились с возможностями работы в системе Mathematica с такими объектами математики, как векторы и матрицы. Мы также научились более умело работать с объектами очень близкого по структуре к спискам класса данных Mathematica — строками.
Вопросы
- Что такое список в Mathematica?
- Какие типы скобок используются при задании списков и работе с ними?
- Какие функции Mathematica предназначены для создания списков?
- В каком виде может быть задан итератор функции Table?
- Что такое вложенный список?
- Раскройте отличие между количеством уровней списка и количеством уровней внутренней формы выражения?
- Что такое длина и глубина списка? Каким образом можно их "измерить"?
- Какие функции Mathematica позволяют узнать, содержатся ли в списке те или иные выражения; позволяют выбрать из списка те или иные выражения?
- Назовите функции Mathematica, позволяющие изменять списки. Какие действия они оказывают на списки?
- Какие функции Mathematica используются при работе с одноуровневыми (векторы) и двухуровневыми (матрицы) списками? Для каких целей?
- Перечислите функции Mathematica, позволяющие работать со строками как со списками.
Упражнения
- Создайте при помощи функции Table следующие списки:
{{1},{1,3},{1,3,5},{1,3,5,7},{1,3,5,7,9},{1,3,5,7,9,11}}
{{1,3,5,7,9,11},{3,5,7,9,11},{5,7,9,11},{7,9,11},{9,11},{11}}
{{11,9,7,5,3,1},{9,7,5,3,1},{7,5,3,1},{5,3,1},{3,1},{1}}
{{11,9,7,5,3,1},{11,9,7,5,3},{11,9,7,5},{11,9,7},{11,9},{11}}
- Создайте одномерный список из 10 элементов, которые случайным образом принимают значения
- +5, 0 и -5;
- +5 и -5 (один из способов — сгенерировать список бинарных значений 0 и 1, которые заменить соответствующим образом заданной парой значений)
- При помощи функции Array создайте список {{f[1,1],f[1,2],f[1,3]},{f[2,1],f[2,2],f[2,3]},{f[3,1],f[3,2],f[3,3]},{f[4,1],f[4,2],f[4,3]}}. Точно такой же список создайте при помощи функции Table.
- Из списка {1,-3,a,0,{a},b,0,0,{},1,{a,-3},-3,b,1} исключите
- все нулевые элементы;
- все элементы, являющиеся отрицательными числами;
- все символьные выражения;
- все выражения, не являющиеся символами.
- Преобразуйте вложенный список {{a,1},{b,2},{c,3},{d,4},{e,5}} в два списка {1,2,3,4,5} и {e,d,c,b,a}.
- Создайте список, элементами которого выступают буквы вашего имени, отчества и фамилии (например, {и,в,а,н,и,в,а,н,о,в,и,ч,и,в,а,н,о,в}).
Выполните следующие задания (в скобках указаны функции Mathematica, которыми следует пользоваться при выполнении задания).
- узнайте, встречаются ли в списке буквы "а", "е", "о ", "и"; если встречаются, то сколько раз и под какими номерами (FreeQ, MemberQ, Count, Position);
- из исходного списка сформируйте список, содержащий в качестве элементов одну из этих букв (Select, Take);
- замените в исходном списке все гласные числом 1, а согласные — числом 0 (ReplacePart, Delete, Insert);
- из исходного списка сформируйте список, содержащий в качестве элементов только буквы отчества (Delete, Drop);
- из списка, полученного в пункте (г), сформируйте новый список, добавив к нему буквы имени и фамилии (Append, Prepend);
- ) поменяйте порядок следования имени, отчества и фамилии в полученном в пункте (д) списке (RotateLeft, RotateRight).
- Убедитесь в том, что выражения {x-5,2*y+h,z} и {7*x-5,y+2*y^2,0.1z-Sqrt[z]} являются векторами, затем, не пользуясь функциями Dot, Cross, найдите их скалярное и векторное произведение. При помощи функций Dot, Cross проверьте результат.
- Убедитесь в том, что выражение {{g,6,u},{4,j,9},{f,2,4}} является матрицей, найдите её определитель и постройте соответствующую ей транспонированную матрицу.