| Россия |
Первое знакомство с Mathematica
1.2. Ввод данных
С правилами ввода арифметических выражений познакомимся, взяв за основу книгу В. П. Дьяконова [2].
Основные математические операции: сложение, вычитание, умножение и деление, — задаются при помощи операторов. Понятие операторов даёт В. П. Дьяконов [2, с. 175]: "Операторы (от слова operator – исполнитель) являются элементами записи математических выражений, указывающими на то, какие действия производятся над символьными или числовыми данными. Когда эти данные используются совместно с операторами, их называют операндами". Основные операторы для выполнения арифметических действий: " + ", " – ", " * ", " / ". Возведение в степень осуществляется при помощи знака возведения в степень " ^ ". Примеры использования некоторых операторов приведены на рис. 1.4.
Однако существуют и альтернативные способы задания простейших операторов (П. Веллин и др. [14, с. 19–20]). Так деление можно записать в традиционной форме, в виде дроби, где делимое находится в числителе над горизонтальной чертой, а делитель — в знаменателе, под горизонтальной чертой. Для этого сперва записывается делимое, затем нажимается комбинация клавиш Ctrl+/, затем вводится делитель.
Подобным же образом можно записать и выражение для возведения в степень: сначала записывается основание, потом нажимается комбинация клавиш Ctrl+^ (на QWERTY-клавиатурах это сочетание Ctrl+Shift+6), потом — показатель степени.
При умножении вместо традиционно используемой в качестве знака умножения звёздочки " * " можно использовать пробел. В поздних версиях Mathematica он автоматически заменяется оператором " x ". Примеры альтернативного ввода операторов см. на рис. 1.5.
Е. М. Воробьёв в книге [1, с. 10] акцентирует внимание читателей на немаловажном вопросе порядка выполнения операций при работе со сложными выражениями. Следует знать, что Mathematica придерживается традиционных представлений о старшинстве арифметических операций. Так, например, вычисление выражения 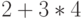 даст 14, а не 20, как при вычислении
даст 14, а не 20, как при вычислении 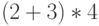 . И всё равно, как советует Е. М. Воробьёв [1, с. 10], "не стоит экономить на круглых скобках ( и ), используемых для группирования" по причине специфического "одноэтажного" характера ввода исходных данных. Чтобы задать выражение
. И всё равно, как советует Е. М. Воробьёв [1, с. 10], "не стоит экономить на круглых скобках ( и ), используемых для группирования" по причине специфического "одноэтажного" характера ввода исходных данных. Чтобы задать выражение 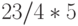 , в Mathematica использование круглых скобок оказывается необходимым:
, в Mathematica использование круглых скобок оказывается необходимым:  . Если ввести
. Если ввести 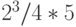 , то это будет воспринято как
, то это будет воспринято как  . Другое выражение, записанное на языке Mathematica как
. Другое выражение, записанное на языке Mathematica как 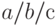 , будет сгруппировано как
, будет сгруппировано как 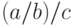 , а выражение
, а выражение 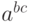 — как
— как 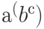 .
.
Вообще для вычислений Mathematica использует 4 вида скобок, каждый из которых имеет определённые неперекрывающиеся функции (С. Вольфрам [15, с. 5–6]):
- круглые скобки ( ), используемые в математических выражениях для группировки отдельных частей выражений;
- квадратные скобки [ ] для функций;
- фигурные скобки { } для списков;
- двойные квадратные [[ ]] для индексирования.
С круглыми скобками мы уже познакомились и знаем, что их назначение то же, что и в математике — задание приоритета математических и логических операций. Квадратные скобки используются для задания аргументов функций. Так, например, для вычисления натурального логарифма вещественного числа 7.62 в окно редактирования следует ввести следующее: Log[7.62]. Следует отметить, что Mathematica различает строчные и прописные буквы, поэтому выражения LOG или log не являются эквивалентами имени Log логарифмической функции (Е. М. Воробьёв [1, с. 11]).
Mathematica содержит огромное количество встроенных функций (команд) — более тысячи. Поэтому, как отмечает Е. М. Воробьёв [1, с. 11], "ее использование как символьного, графического и численного калькулятора сводится в основном к применению различных функций к исходным выражениям, затем к функциям от исходных выражений, затем к функциям от функций от исходных выражений и т.д". Практически невозможно запомнить все имеющиеся в программе функции, способы задания их аргументов, опций и т.д. Однако спасительным в этом случаем является то, что заголовки большинство функций в Mathematica сходны с общепринятыми названиями в англоязычной математической терминологии. Приведём пример. Если возникла необходимость записать число, сопряжённое к тому или иному заданному комплексному числу, вспоминаем или ищем в словаре термин "сопряжённый" на английском языке и пробуем задать функцию в виде Conjugate[expr], где expr — заданное комплексное выражение, и это приводит к искомому результату — см. пример на рис. 1.6.
Для некоторых математических функций, имеющих собственные обозначения, заголовки функций в Mathematica совпадают с этими обозначениями. Среди них — уже известная нам функция извлечения натурального логарифма Log, дифференцирование D, извлечение квадратного корня Sqrt, нахождение определителя (детерминанта) матрицы Det. В процессе изучения курса мы познакомимся и с другими подобными функциями.
Теперь разберёмся с фигурными скобками { }. Они применяются для построения списков. Список — это один из основных типов данных в Mathematica, который используется для записи векторов и матриц любого порядка, а также для записи дополнительных аргументов в таких функциях, как Plot (для построения графиков зависимостей) и Integrate (для интегрирования выражений).
В качестве иллюстрации к упомянутым функциям программы в примерах на рис. 1.7 мы осуществляем операцию поэлементного перемножения двух векторов (см. In[1]), а также строим зависимость некоторой математической функции от аргумента (In[3]), при этом сами функции программы подробнее разберём в последующих лекциях. В примере In[3] в выражении Plot[Cos[3*x]+x,{x,-5,5}] список {x,-5,5} показывает, что функция  должна быть построена для x, принадлежащем к интервалу [-5,5] (включая границы). Mathematica обладает очень мощными возможностями для работы со списками, которые будут рассмотрены в последующих лекциях.
должна быть построена для x, принадлежащем к интервалу [-5,5] (включая границы). Mathematica обладает очень мощными возможностями для работы со списками, которые будут рассмотрены в последующих лекциях.
Теперь же что касается двойных скобок [[ ]]. Они также используются при работе со списками. При помощи них можно обращаться акцентированно к элементу списка с конкретным номером. Так в примере In[2] на рис. 1.7 мы вынуждаем Mathematica показать нам второй по счёту элемент списка, который задан в In[1].