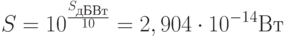|
Здравствуйте. А уточните, пожалуйста, по какой причине стоимость изменилась? Была стоимость в 1 рубль, стала в 9900 рублей. |
Отношение "сигнал-шум" в цифровых системах связи. Построение антенно-фидерных трактов и радиосистем с внешними антеннами
Отношение "сигнал-шум" в цифровых системах связи
Очень важной характеристикой производительности цифровых систем связи является отношение "сигнал-шум".
Отношение "сигнал-шум" - это отношение энергии сигнала на 1 бит к плотности мощности шумов на 1 герц ( 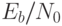 ). Рассмотрим сигнал, содержащий двоичные цифровые данные, передаваемые с определенной скоростью - R бит/с. Напомним, что 1 Вт = 1 Дж/с, и вычислим удельную энергию одного бита сигнала: Eb = STb (где S - мощность сигнала; Tb - время передачи одного бита). Скорость передачи данных R можно выразить в виде
). Рассмотрим сигнал, содержащий двоичные цифровые данные, передаваемые с определенной скоростью - R бит/с. Напомним, что 1 Вт = 1 Дж/с, и вычислим удельную энергию одного бита сигнала: Eb = STb (где S - мощность сигнала; Tb - время передачи одного бита). Скорость передачи данных R можно выразить в виде 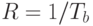 . Учитывая, что тепловой шум, присутствующий в полосе шириной 1 Гц, для любого устройства или проводника составляет
. Учитывая, что тепловой шум, присутствующий в полосе шириной 1 Гц, для любого устройства или проводника составляет
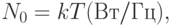 |
( 12.1) |
где N0 - плотность мощности шумов в ваттах на 1 Гц полосы; k - постоянная Больцмана, 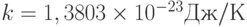 ; T - температура в Кельвинах (абсолютная температура), то, следовательно,
; T - температура в Кельвинах (абсолютная температура), то, следовательно,
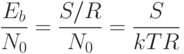 |
( 12.2) |
Отношение 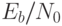 имеет большое практическое значение, поскольку скорость появления ошибочных битов является (убывающей) функцией данного отношения. При известном значении
имеет большое практическое значение, поскольку скорость появления ошибочных битов является (убывающей) функцией данного отношения. При известном значении 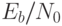 , необходимом для получения желаемого уровня ошибок, можно выбирать все прочие параметры в приведенном уравнении. Следует отметить, что для сохранения требуемого значения
, необходимом для получения желаемого уровня ошибок, можно выбирать все прочие параметры в приведенном уравнении. Следует отметить, что для сохранения требуемого значения 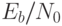 при повышении скорости передачи данных R придется увеличивать мощность передаваемого сигнала по отношению к шуму.
при повышении скорости передачи данных R придется увеличивать мощность передаваемого сигнала по отношению к шуму.
Довольно часто уровень мощности шума достаточен для изменения значения одного из битов данных. Если же увеличить скорость передачи данных вдвое, биты будут "упакованы" в два раза плотнее, и тот же посторонний сигнал приведет к потере двух битов информации. Следовательно, при неизменной мощности сигнала и шума увеличение скорости передачи данных влечет за собой возрастание уровня возникновения ошибок.
Пример 12.1
Рассмотрим метод кодирования сигнала, для которого необходимо, чтобы отношение
равнялось 8,4 дБ при частоте возникновения ошибок 10-4 (ошибочным является 1 бит из каждых 10000). Если эффективная температура теплового шума равна 290 К, а скорость передачи данных - 1 Мбит/с, какой должна быть мощность сигнала, чтобы преодолеть тепловой шум?
Решение:
По формуле (12.2) находим S:
Для упрощения расчетов переведем это выражение в логарифмы:
Так как 1 Мбит = 1048576 бит, то
или
Следовательно, для того чтобы преодолеть тепловой шум, необходима мощность 35,37 дБВт.