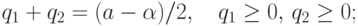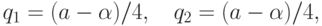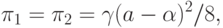Часть плоскости 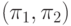 , содержащая решения
неравенств (3.28), отмечена цифрой 1 на рис. рис.1.8.
, содержащая решения
неравенств (3.28), отмечена цифрой 1 на рис. рис.1.8.
Теперь рассмотрим пары (q1,q2), удовлетворяющие условиям
Согласно (3.11),
при

линейный
отрезок (3.27),
лежащий в плоскости
(q1,q2), отображается на
отрезок прямой
 |
(
3.29)
|
При этом случаю
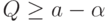
соответствует
отрезок
прямой (3.29), определяемый
условиями

,

(см.
рис.1.5).
Следовательно, часть плоскости
(q1,q2), точки которой
удовлетворяют неравенствам
имеет образ на плоскости
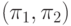
, определяемый условиями
Указанные области помечены цифрой 2 соответственно на
рис.1.5 и на
рис.1.8.
Отрезок прямой (3.29), соответствующий случаю 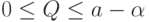 ,
определяется дополнительными условиями
,
определяется дополнительными условиями 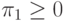 ,
, 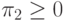 .
При этом
.
При этом
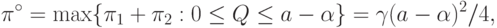 |
(
3.30)
|
причем указанному в (3.3) максимальному значению
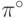
соответствует случай, когда
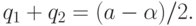 |
(
3.31)
|
Таким образом, часть плоскости
(q1,q2), точки которой
удовлетворяют неравенствам
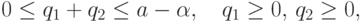 |
(
3.32)
|
имеет образ на плоскости критериев, определяемый условиями
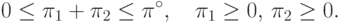 |
(
3.33)
|
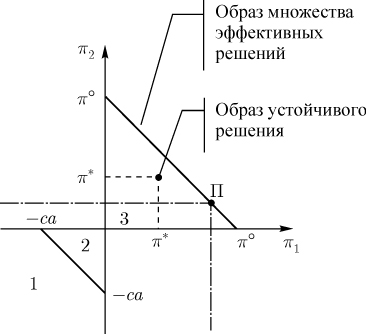
Указанные области (3.32) и (3.33) помечены цифрой 3
соответственно на
рис.1.5 и
рис. 1.8.
Рассмотрим некоторую точку  , лежащую на границе
, лежащую на границе
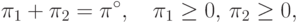 |
(
3.34)
|
выделенной жирной линией на
рис.1.8.
Очевидно, что все точки
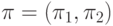
,
лежащие под отрезком (3.34) в пределах прямоугольного
конуса с вершиной в точке
 доминируются
доминируются этой точкой,
т.е.

,

.
При этом сама точка

является
неулучшаемой в пределах образа
первого квадранта плоскости решений
(q1,q2) на плоскости
критериев
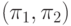
. Следовательно, точки отрезка (3.34)
составляют множество образов всех
оптимальных по Парето
решений для рассматриваемого примера.
Согласно (3.30) и (3.31), множество
всех эффективных решений, являющееся прообразом отрезка (3.34),
составляет отрезок
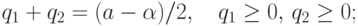 |
(
3.35)
|
см.
рис.1.6. Этот
отрезок не
содержит точки равновесия
(x*,y*) из (3.17).
Соответственно, определяемый условиями (3.19)
образ этой точки, отмеченный на
рис.1.8, не
принадлежит
"паретовской" части границы (3.34).
Замечание 1.12 (о стимулах к кооперации). Рассмотренный
пример показывает, что свойство устойчивости по Нэшу и свойство оптимальности по Парето могут не совмещаться ни в одном решении.
Например, лежащая на отрезке эффективных решений (3.35) точка с координатами
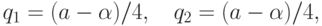 |
(
3.36)
|
образ которой на плоскости критериев принадлежит паретовской
границе (3.34) и имеет
координаты
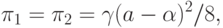 |
(
3.37)
|
обеспечивает обеим фирмам большую
прибыль, чем устойчивое
решение (3.17); ср. (3.19) и (3.37).
Однако решение (3.36) является
неустойчивым при
поведении сторон.
Указанное обстоятельство определяет заинтересованность этих сторон в
обеспечении согласованности действий, направленных на увеличение прибыли.
Анализ практики коллективных действий производителей одного и того же
товара обнаруживает существование многих различных форм такого
сотрудничества, к математическому исследованию проблем которого мы
вернемся в гл. 3.
Картели6, синдикаты7 и тресты8 могут интерпретироваться как организационные
формы, создаваемые в указанных целях.
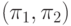 , содержащая решения
неравенств (3.28), отмечена цифрой 1 на рис. рис.1.8.
, содержащая решения
неравенств (3.28), отмечена цифрой 1 на рис. рис.1.8.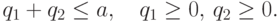
 линейный отрезок (3.27),
лежащий в плоскости (q1,q2), отображается на отрезок прямой
линейный отрезок (3.27),
лежащий в плоскости (q1,q2), отображается на отрезок прямой
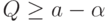 соответствует отрезок
прямой (3.29), определяемый
условиями
соответствует отрезок
прямой (3.29), определяемый
условиями  ,
,  (см.
рис.1.5).
Следовательно, часть плоскости (q1,q2), точки которой
удовлетворяют неравенствам
(см.
рис.1.5).
Следовательно, часть плоскости (q1,q2), точки которой
удовлетворяют неравенствам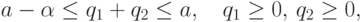
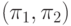 , определяемый условиями
, определяемый условиями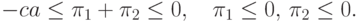
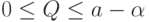 ,
определяется дополнительными условиями
,
определяется дополнительными условиями 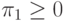 ,
, 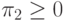 .
При этом
.
При этом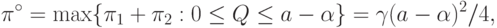
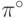 соответствует случай, когда
соответствует случай, когда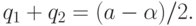
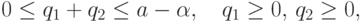
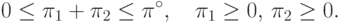
 , лежащую на границе
, лежащую на границе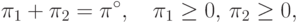
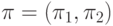 ,
лежащие под отрезком (3.34) в пределах прямоугольного
конуса с вершиной в точке
,
лежащие под отрезком (3.34) в пределах прямоугольного
конуса с вершиной в точке  доминируются этой точкой,
т.е.
доминируются этой точкой,
т.е.  ,
,  .
При этом сама точка
.
При этом сама точка  является неулучшаемой в пределах образа
первого квадранта плоскости решений (q1,q2) на плоскости
критериев
является неулучшаемой в пределах образа
первого квадранта плоскости решений (q1,q2) на плоскости
критериев 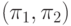 . Следовательно, точки отрезка (3.34)
составляют множество образов всех оптимальных по Парето
решений для рассматриваемого примера.
. Следовательно, точки отрезка (3.34)
составляют множество образов всех оптимальных по Парето
решений для рассматриваемого примера.