Функциональные зависимости и реляционные базы данных

Минимальные покрытия множеств функциональных зависимостей

Попытаемся теперь выяснить, какова роль F -зависимостей в реляционных базах данных. Как показали исследования, класс F -зависимостей оказывает существенное влияние на построение согласованных схем реляционных баз данных, определяет механизмы согласованности данных и целостности баз данных.

Одной из основных целей создания базы данных является сохранение всех данных и взаимосвязей между ними из предметной области в вычислительной среде. Табличное представление отношений в реляционных базах данных позволяет выдвинуть следующую гипотезу хранения данных - каждой ФЗ по отношению. Другой целью создания базы данных является надежность и целостность сохраняемых данных. Можно предположить, что табличное представление породит ряд проблем, связанных с восстанавливаемостью данных, и вступит в противоречие с требованием производительности базы данных. Поэтому меньшее число F-зависимостей означает меньший объем использования памяти компьютера и меньшее число проверок при операциях модификации.

В начале проектирования реляционных баз данных всегда возникает задача представления множеств F -зависимостей. Чем меньшим числом отношений их можно представить, тем лучше. Формализация решения этой задачи строится на понятии покрытия ФЗ. Построение покрытий множеств ФЗ является четвертой (4) конструктивной идеей в теории проектирования реляционных баз данных. Введем ряд определений.

Определение 11. Два множества F-зависимостей F и G над схемой r отношения R эквивалентны, если их замыкания совпадают, т.е. F⁺ = G⁺.

Эквивалентность двух множеств ФЗ F и G устанавливается следующим образом: для каждой ФЗ из F проверяется ее принадлежность G⁺ ; для этого вычисляется Y⁺ ; затем проверяется вложение Z в Y⁺ ; если каждая зависимость F принадлежит G⁺, то каждая зависимость в F⁺ принадлежит G⁺ ; далее повторяем процедуру для G по отношению к F.

Следствием введения понятия эквивалентности является следующий важный факт: каждое множество ФЗ покрывается некоторым множеством ФЗ, в которых ни одна из правых частей не имеет более одного атрибута (правила декомпозиции и объединения). Таким образом, существует набор эквивалентных схем для каждой исходной схемы отношений реляционной базы данных.

Теория проектирования реляционных баз данных дает возможность построения более коротких представлений ФЗ. Для рассмотрения таких процедур введем понятия неизбыточных ФЗ и минимального покрытия множеств ФЗ.

Определение 12. Множество F -зависимостей F неизбыточно, если у него нет собственного подмножества, эквивалентного ему самому.

Определение 13. Множество F -зависимостей F минимально, если оно содержит не больше F-зависимостей, чем любое эквивалентное ему множество.

Минимальное покрытие (МП) не может содержать избыточных зависимостей. Понятие МП F можно детализировать следующим образом:

• правая часть каждой ФЗ в F содержит один атрибут;
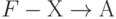• ни для какой ФЗ из F множество не эквивалентно F ;
• ни для какой ФЗ из F и собственного подмножества 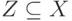множества 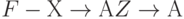не эквивалентны.

Доказано, что для каждого множества ФЗ F существует эквивалентное ему минимальное покрытие. Для заданного F может существовать несколько минимальных покрытий. Ниже приведены общие алгоритмы проверки избыточности и построения минимальных покрытий.

Алгоритмы проверки избыточности

Алгоритм REDUNDANT ( F )
input:		Множество F
output: 	True, если F избыточно
	1.	temp = false
                   for any X ->Y < F do
                         if MEMBER ( F - { X -> Y } , X -> Y )  then temp = True
                         Return ( temp )

Алгоритм NONREDUN ( G )
input:		Множество ФЗ  G
output: 	Неизбыточное покрытие G
	1.	F = G
                   for any X ->Y > G do
                         if MEMBER (F - { X -> Y }, X -> Y ) then
                                 F = F - { X -> Y } 
                                 Return (F)