Функциональные зависимости и реляционные базы данных
Основные классы функциональных зависимостей
Анализ связей между сущностями в предметных областях позволяет выделить различные классы функциональных зависимостей.
Для определения ФЗ предметной области часто бывает недостаточно определить все возможные ключи отношения. Значения атрибутов могут зависеть от ключа по-разному. Различают классы полных и частичных ФЗ. ФЗ может быть частичной, когда значение неключевого атрибута зависит от значений некоторых атрибутов составного ключа, и полной, когда значения неключевого атрибута зависят от значений всех атрибутов составного ключа.
Введем определение.
Определение 3. Говорят, что неключевой атрибут функционально полно зависит от составного ключа, если он функционально зависит от ключа, но не находится в функциональной зависимости ни от какой части составного ключа. Если неключевой атрибут зависит от части составного ключа, то говорят о частичной ФЗ.
Пример. Частичные и полные ФЗ
ПРЕПОДАВАТЕЛЬ_ПРЕДМЕТ (Личный номер, Предмет, Фамилия, Должность, Оклад, Часы)
| 1. | Иванов | доцент | 25000 | Математика | 40 |
| 2. | Исаев | доцент | 25000 | Физика | 50 |
| 3. | Фролов | профессор | 50000 | Химия | 30 |
Первичным ключом отношения ПРЕПОДАВАТЕЛЬ_ПРЕДМЕТ является пара атрибутов Личный_номер-Предмет. Значения атрибута Количество_часов зависят от значения атрибута Предмет, т.е. имеем частичную ФЗ Предмет -> Часы. Значения атрибута Фамилия зависят от значений атрибутов Личный_номер-Предмет, т.е. имеем полную функциональную зависимость {Личный_номер, Предмет} -> Фамилия.
Рассмотрим проблему избыточности данных с точки зрения существования определенных функциональных зависимостей. Избыточность данных может проявляться в виде дублирования значений некоторых атрибутов. Так, например, если несколько преподавателей находятся на одной и той же должности, то их оклады могут совпадать. Атрибут Оклад частично зависит от ключа отношения, но однозначно определяется атрибутом Должность. Разделение исходного отношения на два новых отношения позволит исключить дублирование данных.
Таким образом, выявление определенных функциональных зависимостей в отношениях базы данных позволяет преобразовать их с целью исключения избыточности и повышения надежности данных. Разбиение исходных отношений в соответствии с функциональными зависимостями - это вторая (2) конструктивная идея в теории проектирования реляционных баз данных. Формирование схем отношений путем разбиения исходных отношений по их атрибутам с учетом функциональных зависимостей является одним из способов создания хороших схем реляционных баз данных.
Каким образом можно использовать это наблюдение с учетом семантики данных для конструирования отношений? Имеет смысл разбить все возможные зависимости на определенные типы ФЗ, и на основе этой классификации проанализировать, какие типы ФЗ к каким аномалиям в выполнении реляционных операций приводят. Такой анализ может стать основой для построения алгоритмов проектирования реляционной базы данных.
Анализ связей между сущностями в предметных областях позволяет определить, наряду с частичной и полной ФЗ, еще несколько классов ФЗ. Одним из таких классов является класс транзитивных ФЗ.
Определение 4. Пусть X, Y, Z - атрибуты отношения R. Если при этом имеются ФЗ
и
, но отсутствуют ФЗ
и
, то говорят, что Z транзитивно зависит от Х. Такие ФЗ называются транзитивными (Т-зависимостями).
Пример. Транзитивные ФЗ
Личный номер преподавателя определяет его должность, т.е. имеет место ФЗ Личный_номер -> Должность. С другой стороны, согласно тарификации каждой должности назначается определенный оклад, т.е. имеет место ФЗ Должность -> Оклад. Каждый преподаватель получает за работу соответствующий должности оклад, т.е. оклад преподавателя определяется через его должность.
Очевидно, что семантическая связь между атрибутами отношения может носить неоднозначный характер, это порождает существование класса многозначных зависимостей (MV-зависимостей). Например, один преподаватель может преподавать несколько предметов, а один предмет может преподаваться несколькими преподавателями. Многозначная зависимость может быть следующих типов: 1:N (один ко многим), M:1 (многие к одному) и M:N (многие ко многим).
Определение 5. Пусть r - некоторая схема отношения, X и Y - подмножества атрибутов r. Если при заданных значениях атрибутов из {X} существует некоторое множество, состоящее из нуля или более взаимосвязанных значений атрибутов из {Y}, никак не связанных со значениями других атрибутов этого отношения r - X - Y, то говорят о существовании многозначной зависимости между атрибутами X и Y:
(класс MV-зависимостей).
Формально многозначная зависимость означает, что если в отношении 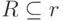 имеются два кортежа t и s, такие, что их значения совпадают по атрибутам из Х, т.е. t[X] = s[X], то данное отношение содержит кортежи w и v, такие, что
имеются два кортежа t и s, такие, что их значения совпадают по атрибутам из Х, т.е. t[X] = s[X], то данное отношение содержит кортежи w и v, такие, что
- w[X] = v[X] = t[X] = s[X],
- w[Y] = t[Y], w[r - X - Y] = s[r - X - Y],
- v[Y] = s[Y], v[r - X - Y] = t[r - X - Y].
Фактически многозначная зависимость означает, что значения атрибутов из Y в кортежах t и s можно поменять местами и получить два новых кортежа, также принадлежащих отношению R.
Разделение установленных функциональных зависимостей по различным отношениям может привести к нарушению принципа замкнутости реляционных операций, потере некоторых существующих кортежей или появлению мнимых кортежей. Это обстоятельство приводит к необходимости выделения еще одного класса функциональных зависимостей - класса зависимостей по соединению ( J -зависимостей). Этот класс ФЗ требует от ФЗ наличия свойства восстанавливаемости по своим проекциям с помощью естественного соединения.
Пусть U - универсальное отношение, полученное объединением всех атрибутов сущностей предметной области в одно отношение.
Определение 6. Пусть r = {r_1, …, r_p} - множество схем на U. Отношение R \subset U удовлетворяет зависимости по соединению, если R разлагается без потерь на r как
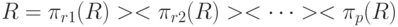
Процесс выделения новых классов функциональных зависимостей может быть продолжен. Он аналогичен классификации чисел в школьном курсе алгебры: натуральные числа -> целые числа -> рациональные числа -> действительные числа. В теории реляционных баз данных уже выделены ветвящиеся и циклические функциональные зависимости, предпринимаются попытки расширить набор реляционных операций. Введение новых классов функциональных зависимостей обусловлено следующим важным обстоятельством: при декомпозиции схем реляционных отношений могут быть потеряны как функциональные зависимости, так и кортежи (или приобретены несуществующие кортежи). Каждый класс функциональных зависимостей позволяет проанализировать механизм потери данных или функциональной зависимости и сформулировать правила, которые позволят этого избежать.
Однако для практических целей проектирования реляционных баз данных достаточно знания рассмотренных классов ФЗ. Даже зависимость по соединению встречается очень редко.

