|
Не могу найти требования по оформлению выпускной контрольной работы по курсу профессиональной переподготовки "Менеджмент предприятия" |
Обоснование инвестиционных решений в условиях определенности
Рассмотрим эту методику расчета ARR на конкретном примере (табл. 9.15).
При начислении амортизации по ставке 20%, среднегодовая сумма чистой прибыли составит 7,904 млн. руб. (39,52 / 5), а средняя стоимость инвестиций 25 млн. руб. ((50 + 0) /2). Тогда
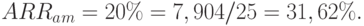
Соответствующие расчеты для 10%-ой амортизации будут иметь следующий вид:
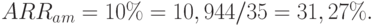
Наиболее распространенный способ использования показателя ARR заключается в сравнении его величины с рентабельностью всех активов (или инвестированного капитала) предприятия в целом. Руководство компании может установить некоторые пороговые значения данных показателей для сопоставления с учетной доходностью новых инвестиций. Например, в качестве норматива может быть принята доходность 25%. Тогда оба варианта рассматриваемого нами проекта будут удовлетворять критерию требуемой рентабельности и проект может быть одобрен.
В качестве пороговых значений могут быть использованы фактические данные, достигнутые предприятием в предыдущие периоды, среднеотраслевые показатели рентабельности или какие-либо еще нормативы. Общей чертой всех этих показателей будет являться их "бухгалтерское" происхождение, возможность рассчитать их значения по данным стандартной финансовой отчетности. Данная возможность может показаться большим преимуществом показателя ARR, методика расчета которого практически полностью совпадает с методикой вычисления общеизвестных финансовых коэффициентов. На самом деле, именно в этом и заключается основной недостаток учетной доходности. Ради обеспечения методического "родства" с ее бухгалтерскими аналогами приходится отказываться от дисконтирования денежных потоков и заменять показатели движения денежных средств на показатели бухгалтерской чистой прибыли. По сути дела, это означает отказ от фундаментальных положений финансовой теории, лежащих в основе инвестиционного анализа. Вместо очевидных и однозначно измеряемых величин денежных потоков, разработчики проекта должны будут ориентироваться на весьма туманный и пока еще никем точно не определенный бухгалтерский показатель чистой прибыли, расчет фактической величины которого базируется на многочисленных субъективных предположениях и приблизительных оценках будущего. Здесь уместно вспомнить древнюю финансовую мудрость: "Прибыль это мнение, а денежные потоки это факт". Вряд ли можно признать разумной ориентацию не на реальные факты, а на субъективные мнения. Тем более, в такой ответственной сфере, как обоснование инвестиционных решений.
Значительно более обоснованным с теоретической точки зрения является другой относительный показатель экономической эффективности инвестиций – индекс рентабельности (Profitability Index, PI). Для его расчета сумма дисконтированных денежных притоков по проекту 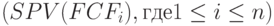 делится на величину первоначальных инвестиций в проект (
делится на величину первоначальных инвестиций в проект ( 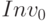 ). Для нахождения величины числителя дроби, воспользуемся данными табл. 9.14, в которой рассчитана накопленная сумма всех денежных потоков, включая инвестиции (то есть, NPV проекта). Исключив из итоговой цифры сумму первоначальных инвестиций, получим искомое значение
). Для нахождения величины числителя дроби, воспользуемся данными табл. 9.14, в которой рассчитана накопленная сумма всех денежных потоков, включая инвестиции (то есть, NPV проекта). Исключив из итоговой цифры сумму первоначальных инвестиций, получим искомое значение 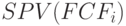 . Для варианта с начислением амортизации по ставке 20% оно составит 88,19 млн. руб. ((38,19 – (-50)), в случае более низких амортизационных отчислений (по ставке 10%)
. Для варианта с начислением амортизации по ставке 20% оно составит 88,19 млн. руб. ((38,19 – (-50)), в случае более низких амортизационных отчислений (по ставке 10%)  . Величина первоначальных инвестиций (Inv0) остается неизменной для обоих вариа
нтов – 50 млн. руб. Рассчитаем значения PI для каждого из рассмотренных вариантов:
. Величина первоначальных инвестиций (Inv0) остается неизменной для обоих вариа
нтов – 50 млн. руб. Рассчитаем значения PI для каждого из рассмотренных вариантов:
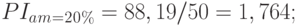
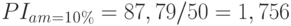 .
.
По методике расчета, рентабельность инвестиций очень близка к показателю чистой приведенной стоимости (NPV). Она дополняет этот показатель, так как позволяет учитывать соответствие масштабов первоначальных инвестиций и итоговой NPV. Например, одна и та же величина чистой приведенной стоимости (допустим, 2 млн. руб.) может быть обеспечена проектом А с первоначальными инвестициями 1 млн. руб. и проектом Б, в который вложены 5 млн. руб. Приведенная стоимость будущих денежных притоков ( 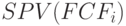 ) по проекту А составит 3 млн. руб.( (2 – (-1)), а по проекту Б 7 млн. руб. ((2 – (-5)). Тогда PIА = 3 (3 / 1), а PIБ = 1,4 (7 / 5). Очевидно, что реальная экономическая отдача от проекта А значительно выше.
) по проекту А составит 3 млн. руб.( (2 – (-1)), а по проекту Б 7 млн. руб. ((2 – (-5)). Тогда PIА = 3 (3 / 1), а PIБ = 1,4 (7 / 5). Очевидно, что реальная экономическая отдача от проекта А значительно выше.
Следует подчеркнуть, что ценность показателя PI заключается именно в его "дополнительности" к основному критерию эффективности инвестиций NPV. В рассмотренном нами примере с проектами А и Б сумма чистой приведенной стоимости (2 млн. руб.) была одинаковой для обоих проектов. Поэтому возникла необходимость в углублении анализа. Если бы эти проекты были альтернативными, то величина индекса рентабельности позволила бы сделать правильный выбор: проект А следовало признать лучшим, так как он обеспечивал бы акционерам ту же самую NPV при значительно меньшем объеме первоначальных вложений (1 млн. руб. против 5 млн. руб.). Но конечной целью любого бизнеса является максимизация стоимости вложенного капитала, то есть, увеличение NPV инвестиций. Поэтому из двух проектов с различными NPV следует выбирать тот, который обеспечивает получение большей чистой приведенной стоимости. В этом случае критерий NPV получает приоритет над показателем PI, так как он наиболее точно отражает величину абсолютного прироста богатства инвесторов.
Например, инвестиции в сумме 1 тыс. руб. могут обеспечить достижение 500%-ой рентабельности (PI = 5). Но в абсолютном выражении это будет означать прирост богатства инвесторов всего лишь на 4 тыс. руб. ( 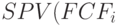 ) этих инвестиций составит 5 тыс. руб. (1 * 5), соответственно, NPV будет равна 4 тыс. руб. (5 – 1)). В то же время, вложение 1 млн. руб. в проект с достаточно "скромным" PI = 1,5, будет означать абсолютный прирост богатства в сумме 500 тыс. руб. (SPV(FCFi) = 1,5 тыс. руб. (1 * 1,5), NPV = 0,5 млн. руб. (1,5 – 1)). Ориентируясь только на проекты с максимальным индексом рентабельности, предприятие будет "пропускать" возможности более масштабного увеличения богатства своих владельцев. Конечно, для получения более весомой NPV потребуется вкладывать больше капитала (которого у владельцев может и не оказаться). Но здесь следует вспомнить о возможности привлечения заемных источников финансирования, то есть – о финансовом леверидже. Данная возможность противоречит
нашему исходному предположению о простой структуре капитала. Но даже не отказываясь от принятого нами ограничения, можно предположить, что заем будет сделан не самим предприятием (корпорацией), а ее владельцами. В этом случае структура капитала предприятия по-прежнему не будет включать заемных источников.
) этих инвестиций составит 5 тыс. руб. (1 * 5), соответственно, NPV будет равна 4 тыс. руб. (5 – 1)). В то же время, вложение 1 млн. руб. в проект с достаточно "скромным" PI = 1,5, будет означать абсолютный прирост богатства в сумме 500 тыс. руб. (SPV(FCFi) = 1,5 тыс. руб. (1 * 1,5), NPV = 0,5 млн. руб. (1,5 – 1)). Ориентируясь только на проекты с максимальным индексом рентабельности, предприятие будет "пропускать" возможности более масштабного увеличения богатства своих владельцев. Конечно, для получения более весомой NPV потребуется вкладывать больше капитала (которого у владельцев может и не оказаться). Но здесь следует вспомнить о возможности привлечения заемных источников финансирования, то есть – о финансовом леверидже. Данная возможность противоречит
нашему исходному предположению о простой структуре капитала. Но даже не отказываясь от принятого нами ограничения, можно предположить, что заем будет сделан не самим предприятием (корпорацией), а ее владельцами. В этом случае структура капитала предприятия по-прежнему не будет включать заемных источников.
Ближайшей "родственницей" NPV является внутренняя норма доходности (IRR), подробно рассмотренная нами во втором параграфе данной лекции. Если судить по популярности использования этих двух показателей в практике инвестиционных расчетов, то IRR оставит чистую приведенную стоимость далеко позади себя. Многих бизнесменов привлекает возможность осуществлять прямое сравнение величины IRR с другими показателями доходности или цены (издержек по привлечению) капитала. Популярность внутренней нормы доходности объясняется также и общей склонностью представителей делового мира к использованию относительных показателей: рентабельность, процентная ставка и т.п. Как уже отмечалось в §2, в большинстве случаев использование IRR обусловливает получение результатов, абсолютно идентичных тем, которые были бы получены с применением NPV. Превышение уровня доходности инвестиций над величиной затрат по привлечению (цены) капитала является столь же надежным критерием экономической эффективности проекта, как и его (проекта) положительная чистая приведенная стоимость. Внутренняя норма доходности проекта, рассмотренного в нашем сквозном примере, составила 22,89% для варианта с начислением амортизации по ставке 20% и 22,2% при начислении 10%-ой амортизации 6Данные результаты могут быть получены путем применения финансовой функции ВНДОХ (ВСД в более поздних версиях), встроенной в популярный программный пакет MS Excel, к денежным потокам по проекту (см., например, данные по гр. 2 и 3 табл. 9.13)..
Тем не менее, существуют серьезные "противопоказания" использованию IRR в качестве основного (а тем более – единственного) критерия эффективности инвестиций. Во-первых, довольно часто компьютерные программы могут возвращать множественное значение IRR (или не возвращать ни одного). Уравнение, по которому вычисляется внутренняя норма доходности, имеет единственное решение только в том случае, когда исходный денежный поток строится по стандартной схеме: сначала инвестиции (отток денег), а потом конечная последовательность положительных значений, отражающих денежные притоки по проекту. Если конкретным проектом предусматривается денежный поток, отличный от данной схемы (например, кроме первоначальных инвестиций, возникают оттоки денег в ходе реализации проекта), то расчет единственного значения IRR становится попросту невозможным. По мере увеличения количества перемены знаков перед членами денежного потока (переходов от притоков к оттокам денег) будет увеличиваться число возможных вариантов решения исходного уравнения.
Во-вторых, проекты, по которым получение положительных денежных потоков (притоков денег) выпадает на более ранние периоды, будут выглядеть более привлекательными по критерию IRR, чем по NPV. Это происходит потому, что дисконтирование денежных потоков при расчете чистой приведенной стоимости осуществляется по процентной ставке, равной альтернативным издержкам по привлечению капитала (например – по средневзвешенной цене капитала, WACC). Проекты с положительной NPV будут иметь внутреннюю норму доходности, превышающую WACC. Но внутренняя норма доходности по своей сути также является ставкой дисконтирования, приравнивающей приведенную стоимость будущих денежных притоков к сумме сегодняшних инвестиций. Таким образом, чем выше IRR, тем сильнее будут дисконтироваться более отдаленные денежные притоки по проекту. Следовательно, долгосрочные проекты, предусматривающие получение основной части денежных доходов в последние годы реализации будут иметь высокую NPV и относительно небольшую внутреннюю норму доходности (хотя и превышающую WACC). И наоборот – проекты, по которым основная часть денежных поступлений приходится на первые годы их осуществления, будут иметь непропорционально высокую IRR в сравнении с относительно более скромной NPV. Такое, на первый взгляд, незначительное противоречие может оказать решающее влияние при выборе конкретных проектов, особенно, если этот выбор производится на альтернативной основе. Ориентируясь только на NPV, можно выбрать проект с более низкой чистой приведенной стоимостью, то есть, упустить возможность более выгодного (для владельцев предприятия) инвестирования капитала.
Отмеченный выше недостаток показателя IRR имеет серьезные методические последствия. Экономический смысл дисконтирования заключается в учете альтернативных издержек, связанных с отвлечением капитала на финансирование данных инвестиций. Эти издержки отражают утраченную выгоду вследствие отказа от каких-либо альтернативных возможностей вложения капитала, которые гарантируют получение заданного дохода. Величина ставки дисконтирования определяется именно уровнем этих альтернативных издержек. Поэтому она и называется "ценой капитала" или WACC. Дисконтируя денежные потоки по средней цене капитала, мы по умолчанию предполагаем, что предприятие располагает возможностью реинвестировать свободные денежные потоки по проекту с доходностью, равной этой цене (WACC).
При расчете внутренней нормы доходности дисконтирование осуществляется не по WACC, а по более высокой IRR, то есть предполагается, что у предприятия имеются возможности реинвестировать заработанные доходы по ставке более высокой, чем WACC. Но это невозможно по определению, так как средняя цена капитала как раз и отражает имеющиеся у предприятия альтернативные возможности использования капитала. Таким образом, чем выше IRR проекта, тем существеннее риск переоценки его инвестиционных возможностей. Высокий уровень внутренней доходности может отражать не только уникальную эффективность анализируемого проекта, но и методические недостатки самого показателя, используемого в качестве критерия. Поэтому, в отношениях с такой капризной особой, которой, как выяснилось, является в реальности IRR, следует быть чрезвычайно осторожным. Именно к этому призывают консультанты компании МакКинси (McKinsey), выполнившие глубокий анализ данного аспекта проблемы IRR. Рекомендую ознакомиться с соответствующей статьей, которая опубликована уже в нескольких весьма солидных финансово-экономических изданиях.
В качестве одного из "противоядий" столь коварному свойству внутренней нормы доходности предлагается расчет различных модификаций этого показателя. Одной из популярных версий модифицированной внутренней нормы доходности (MIRR) является показатель, вычисляемый путем решения следующего уравнения:
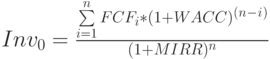 |
( 17) |
Обозначив числитель дроби FV (Future Value), и решив уравнение относительно MIRR, получаем:
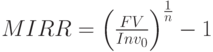 |
( 18) |
В нашем сквозном примере наращенная по средней цене капитала ( 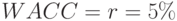 ) будущая стоимость денежных притоков по проекту
) будущая стоимость денежных притоков по проекту 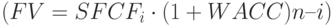 составит:
составит:
- для am = 20% 112,5528 млн. руб.;
- для am = 10% 112,0482 млн. руб. (расчеты этих цифр рекомендуется выполнить самостоятельно).
Подставляя полученные данные в (18), получаем:
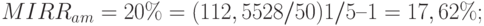
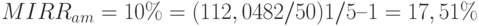 .
.
Сторонники данного показателя указывают на такие его преимущества, как использование цены капитала (WACC), а не IRR для учета возможностей реинвестирования заработанных денег, легкость расчета и отсутствие множественности значений. В то же время, даже самые ярые приверженцы данного подхода не могут не признать, что при определенных условиях (например, большое различие в сроках анализируемых проектов) критерий MIRR может вступать в противоречие с показателем NPV. Но ведь именно в этом и состоит главный недостаток IRR, для устранения которого вводился модифицированный критерий.
Стремление модифицировать изобретенные кем-то другим показатели вообще свойственно многим ученым. Само по себе, оно заслуживает только одобрения. Но при этом следует придерживаться одного важного условия: любая модификация должна базироваться на солидном теоретическом фундаменте. В случае с рассмотренной нами модификацией показателя IRR какого-либо серьезного теоретического обоснования не просматривается. Не удивительно, что предлагаемый вариант ненамного лучше (а скорее даже и хуже, потому что сама по себе (немодифицированная) IRR имеет достаточно серьезное теоретическое обоснование) заменяемого. Остается только добавить, что чрезмерное внимание вопросам реинвестирования заработанных доходов также может отвлечь внимание от главной цели инвестирования – максимизации релевантных денежных потоков именно по данному проекту. В этой связи стоит вспомнить еще одну финансовую мудрость (в трактовке Р. Брейли и С. Майерса): " Никогда ожидаемая доходность других инвестиций не должна влиять на данное инвестиционное решение" 7Р. Брейли, С. Майерс "Принципы корпоративных финансов". – М.: "Олимп-Бизнес", 1997, стр. 89..
Из всего вышесказанного со всей очевидностью вытекает следующий вывод: критерий NPV лучше любых других известных в настоящее время показателей, используемых для оценки экономической эффективности. На этот критерий следует ориентироваться при обосновании подавляющего большинства видов и типов инвестиционных проектов (о возможных исключениях из данного правила будет рассказано в последующих лекциях). Тем не менее, нельзя умолчать о таком важном достоинстве показателя IRR, как возможность его расчета при отсутствии информации о величине альтернативных издержек привлечения (цены) капитала. Чистая приведенная стоимость не может быть рассчитана без знания WACC, в то время как для расчета внутренней нормы доходности достаточно иметь информацию только об исходном денежном потоке. Данное преимущество показателя IRR используется при первичном отборе инвестиционных проектов для формирования бюджета капвложений.
На этом мы заканчиваем лекцию, посвященную обоснованию инвестиционных решений в условиях определенности и в предположении наличия простой структуры капитала. Но это вовсе не означает, что мы завершаем изучение затронутой темы. Наоборот, ознакомление с фундаментальными принципами оценки инвестиций является лишь первым шагом в данном направлении. В последующих лекциях будут рассмотрены методы учета неопределенности будущего при прогнозировании денежных потоков по проекту, способы оценки влияния на чистую приведенную стоимость изменений в структуре капитала, основные подходы к определению величины ставки дисконтирования денежных потоков.


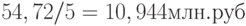 .;
.;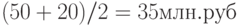 .;
.;