Построение цикла с помощью инварианта
Вычисление логарифма без использования разложения в ряд
Схема построения цикла с помощью инварианта позволяет легко написать алгоритм вычисления логарифма заданного числа без использования разложения в ряд.
Пусть задано вещественное число x. Требуется вычислить логарифм числа x по основанию a c точностью 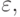 где
где  - некоторое положительное очень маленькое число. Для определенности, пусть a>1 (для a<1 можно воспользоваться тождеством log1/ax = -logax ).
- некоторое положительное очень маленькое число. Для определенности, пусть a>1 (для a<1 можно воспользоваться тождеством log1/ax = -logax ).
Из определения логарифма следует, что надо найти число y такое, что
ay = x.
Нам достаточно, чтобы это равенство выполнялось приближенно. В качестве инварианта используем условие
ayzt = x = const.
Таким образом, в цикле будут меняться три переменные
(y,z,t),
и инвариант записывается в виде
I(y,z,t): ayzt = x
Начальные значения переменных y, z, t выбираются так, чтобы выполнялся инвариант:
y0 = 0, z0 = x, t0 = 1.
Определим условие завершения цикла Q(y,z,t). Необходимо, чтобы искомая величина по окончанию цикла содержалась в переменной y. Следовательно, величина zt должна быть близка к единице: тогда приблизительно выполняется равенство
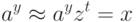
т.е. y приближенно равен искомому логарифму. Для того, чтобы величина zt была близка к единице, нужно, чтобы показатель степени t был близок к нулю, а основание z было не очень велико и не очень мало. Для этого достаточно выполнения трех неравенств
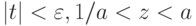
Можно доказать строго, что при выполнении этих неравенств, а также условия ayzt = x, величина y отличается от logax не больше чем на 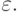
Выполнение этих трех неравенств и являются условием завершения цикла:

Наконец, тело цикла должно преобразовывать переменные (y,z,t) так, чтобы абсолютная величина t монотонно убывала, а переменная z рано или поздно попадала бы в интервал (1/a,a), и при этом сохранялся инвариант. Такое преобразование T легко выписывается по инварианту цикла:
T(y,z,t) = (y+t, z/a, t), если z >= a T(y,z,t) = (y-t, z*a, t), если z <= 1/a T(y,z,t) = (y, z*z, t/2), если 1/a < z < a
Заметим, что при применении преобразования T некоторая величина как бы перетекает из одних переменных в другие, при этом равенство ayzt = x остается неизменным.
Теперь можно выписать алгоритм вычисления логарифма:
вещ алгоритм логарифм(вх: вещ x, вещ a, вещ eps) | дано: x > 0, a > 1, eps > 0 | надо: вычислить log_a x с точностью eps начало алгоритма | вещ y, z, t; | | // инициализация | y := 0.0; z := x; t := 1.0; | утверждение: a^y * z^t == x; | | цикл пока |t| >= eps или z <= 1.0/a или z >= a | | инвариант: a^y * z^t == x; | | если z >= a | | | то | | | z := z/a; y := y + t; | | иначе если z <= 1.0/a | | | то | | | z := z*a; y := y - t; | | иначе | | | z := z*z; t := t/2.0; | | конец если | конец цикла | | утверждение: |t| < eps и | z > 1.0/a и z < a и | a^y * z^t == x; | ответ := y; конец алгоритма

