Построение цикла с помощью инварианта
Алгоритм Евклида вычисления наибольшего общего делителя
Пусть даны два целых числа m и n, хотя бы одно из которых не равно нулю. Требуется найти их наибольший общий делитель. Напомним, что наибольшим общим делителем двух чисел m и n называется такой их общий делитель d, который делится на любые другие общие делители d'. Такое определение НОД подходит не только для чисел, но и для многочленов, поскольку в нем не используется сравнение по величине. Наибольший общий делитель определен с точностью до обратимого множителя; в частности, поскольку в кольце чисел обратимы только элементы  , НОД целых чисел определен с точностью до знака.
, НОД целых чисел определен с точностью до знака.
В качестве пространства X рассматривается множество пар целых чисел
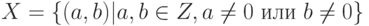
Надо вычислить НОД для заданной пары чисел (m,n). В качестве инварианта используем утверждение, что НОД текущей пары чисел равен НОД исходной пары:
I(a,b): НОД(a,b) = НОД(m,n).
Следовательно, цикл надо строить таким образом, чтобы при изменении переменных a, b наибольший общий делитель пары (a,b) оставался неизменным. В качестве начальной точки x0 используется пара (m,n).
Обозначим через r остаток от деления a на b:
a = gb+r, где |r| < |b|.
Тогда нетрудно доказать, что НОД(b,r) = НОД(a,b). Достаточно показать, что множества общих делителей пары (b,r) и пары (a,b) совпадают. Пусть d делит b и r. Тогда из равенства a = gb+r вытекает, что d делит a. Обратно, пусть d делит a и b. Из определения остатка имеем:
r = a-gb.
Так как правая часть равенства делится на d, то r тоже делится на d.
Итак, при замене пары (a,b) на пару (b,r) НОД не меняется. Обозначим через T отображение
T:(a,b) -> (b,r)
Условие I(a,b) является инвариантным для отображения T.
Осталось только определить условие завершения цикла Q(a,b). Выполнение этого условия должно обеспечивать решение задачи, т.е. нахождение HOД чисел a, b. Для какой пары чисел их НОД можно сразу вычислить? Проще всего, когда одно из чисел равно нулю. В этом случае
НОД(a,0) = a
Итак, в качестве условия завершения цикла используем условие, что вторая компонента пары (a, b) нулевая:
Q(a,b): b = 0
Теперь можно выписать алгоритм нахождения наибольшего общего делителя:
цел алгоритм НОД(вх: цел m, цел n) | дано: целые числа m, n, хотя бы одно отлично от нуля | надо: вычислить наибольший общий делитель пары (m, n) начало алгоритма | цел a, b, r; | // инициализация | a := m; b := n; | утверждение: НОД(a, b) == НОД(m, n); | | цикл пока b != 0 | | инвариант: НОД(a, b) == НОД(m, n) | | r := a % b; // находим остаток от деления a на b | | a := b; b := r; // заменяем пару (a, b) на (b, r) | конец цикла | | утверждение: b == 0 и НОД(a, b) == НОД(m, n); | ответ := a; конец алгоритма
Алгоритм Евклида - один из самых замечательных алгоритмов теории чисел и программирования. Работает он исключительно быстро, за время, линейно зависящее от длины записи входных чисел. (Действительно, легко показать, что за два выполнения тела цикла число b уменьшается не менее, чем в четыре раза. Следовательно, число выполнений тела цикла в худшем случае равно длине двоичной записи максимального из чисел a, b.) Это позволяет применять алгоритм Евклида к очень большим целым числам - например, к двухсотзначным десятичным. Алгоритм Евклида (более точно, расширенный алгоритм Евклида, который будет рассмотрен ниже) применяется для таких больших чисел в схеме кодирования с открытым ключом RSA, которая в настоящее время широко используется на практике для защиты информации.

