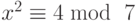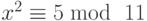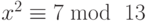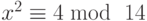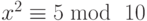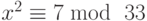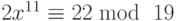|
Прошел экстерном экзамен по курсу перепордготовки "Информационная безопасность". Хочу получить диплом, но не вижу где оплатить? Ну и соответственно , как с получением бумажного документа? |
Опубликован: 19.01.2010 | Уровень: специалист | Доступ: платный
Лекция 13:
Квадратичное сравнение
13.3. Рекомендованная литература
Нижеследующие книги и сайты дают более детальную информацию о предметах, рассмотренных в этой лекции. Пункты, приведенные в квадратных скобках, содержатся в списке в конце книги.
Книги
[Ros06] [Cou99], [BW00] и [Bla03] — для тем, которые обсуждаются в этой лекции.
Сайты
Нижеследующие сайты дают больше информации о темах, обсужденных в этой лекции.
- http://en.wikipedia.org/wiki/Prime_number
- http://primes.utm.edu/mersenne/
- http://en.wikipedia.org/wiki/Primality__test
- www..cl.cam.ac.uk/~jehl004/research/talks/miller-talk.pdf
- http://mathworld.wolfram.com/TotientFunction.html
- http: // en.wikipedia.org/wiki/Proofs_of_Fermat's_little_theorem
- faculty.cs.tamu.edu/klappi/629/analytic.pdf
13.4. Итоги
- Положительные целые числа могут быть разделены на три группы: число 1, простые числа и составные объекты. Положительное целое число — простое число, такое и только такое, если оно точно делится без остатка на два различных целых числа, а именно на 1 и непосредственно само на себя. Составной объект — положительное целое число по крайней мере с двумя делителями.
- Эйлеровская phi -функция
 , которую иногда называют функцией-тотиентом Эйлера, играет очень важную роль в криптографии. Функция указывает число целых чисел, которые меньше чем n и являются взаимно простыми с n.
, которую иногда называют функцией-тотиентом Эйлера, играет очень важную роль в криптографии. Функция указывает число целых чисел, которые меньше чем n и являются взаимно простыми с n. - В таблице 13.6 показаны малая теорема Ферма и теорема Эйлера, которые рассмотрены в этой лекции.
- Чтобы получить большое простое число, мы выбираем большое случайное число и проверяем его — убеждаемся, что оно простое. Алгоритмы, которые решают эту проблему, могут быть разделены на две обширные категории: детерминированные алгоритмы и вероятностные алгоритмы. Некоторые вероятностные алгоритмы для испытания простоты чисел – это испытание Ферма, испытание квадратного корня и испытание Миллера-Рабина. Некоторые детерминированные алгоритмы — испытание на делимости и AKS-алгоритм.
- Согласно основной теореме арифметики, любое положительное целое число, большее, чем 1, может быть разложено на множители в виде простых чисел. Мы рассмотрели несколько методов разложения на множители, включая проверку делением — Ферма, метод Полларда p – 1, метод РО (
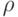 ) Полларда, квадратичное решето и решето поля чисел.
) Полларда, квадратичное решето и решето поля чисел. - Китайская теорема об остатках (Chinese Reminder Theorem — CRT) используется, чтобы решить систему уравнений для вычетов с одной переменной, но с различными взаимно простыми модулями.
- Мы рассмотрели решение квадратичного сравнения по модулю в виде простого числа и квадратичного сравнения по составному модулю. Однако, если модуль является большим, решение квадратичного сравнения по сложности совпадает с разложением модуля на множители.
- В криптографии применяется операция по модулю — возведение в степень. Для быстрого возведения в степень можно использовать метод "возведения в квадрат и умножения". Криптография также включает модульные логарифмы. Если возведение в степень применяется, чтобы зашифровать или расшифровывать информацию, то противник может использовать логарифмы для организации "атаки". Сложность операции, обратной возведению в степень, велика. Хотя возведение в степень может быть сделано с помощью быстрого алгоритма, применение модульного логарифма для больших значений модуля имеет ту же сложность, что и проблема разложения на множители.
13.5. Набор для практики
Обзорные вопросы
- Объясните разницу между простым числом и составным целым числом.
- Определите взаимно простые числа и их свойства.
- Определите следующие функции и их приложения:
-
 функция
функция - Функция (тотиент) Эйлера
-
- Объясните "решето Эратосфена" и его приложения.
- Определите малую теорему Ферма и объяснить ее приложения.
- Определите теорему Эйлера и объясните ее приложения.
- Что такое простые числа Мерсенны? Что такое простые числа Ферма?
- Объясните разницу между детерминированными и вероятностными алгоритмами для определения простых чисел.
- Перечислите некоторые алгоритмы для разложения на множители простых чисел.
- Определите Китайскую теорему об остатках и ее приложения.
- Определите квадратичное сравнение и важность вычетов (QRs) и невычетов (QNRs) в решении квадратных уравнений.
- Определите дискретные логарифмы и объяснить их важность в решении логарифмических уравнений.
Упражнения
- Используя аппроксимацию, найдите:
- число простых чисел между 100 000 и 200 000.
- число составных целых чисел между 100 000 и 200 000
- отношение простых чисел к составным в вышеупомянутом диапазоне и сравните это с тем же самым между 1 – 10.
- Найти наибольший простой сомножитель следующих составных целых чисел: 100, 1000, 10 000, 100 000 и 1 000 000. Также найти наибольший простой сомножитель 101, 1001, 10 001, 100 001 и 1 000 01.
- Покажите, что каждое простое число может быть представлено в форме либо 4k + 1, либо 4k + 3, где k — положительное целое число.
- Найдите некоторые простые числа в форме 5k + 1, 5k + 2, 5 k + 3 и 5k + 4, где k: является положительным целым числом.
- Найдите значение
 ,
,  ,
,  ,
,  ,
, 
- Покажите, что 224 – 1 и 216 – 1 – составные числа. Подсказка: используйте выражение (a2 – b2).
- Есть предположение, что каждое целое число, большее, чем 2, может быть представлено как сумма двух простых чисел. Проверьте это предположение для 10, 24, 28 и 100.
- Есть предположение, что есть много простых чисел в форме n2 + 1. Найдите некоторые из них.
- Найдите результаты после использования малой теоремы Ферма:
- 515 mod 13
- 1518 mod 17
- 45617 mod 17
- 145 mod 101
- Найдите, используя Малую теорему Ферма, результаты выражений, приведенных ниже:
- 5-1 mod 13
- 15-1 mod 17
- 27-l mod 41
- 70-1 mod 101
Обратите внимание, что все модули — простые числа.
- Найдите, используя теорему Эйлера, результаты выражений, приведенных ниже:
- 12-1 mod 77
- 16-1 mod 323
- 20-1 mod 403
- 44-1 mod 667
Обратите внимание, что
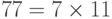 ,
, 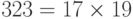 ,
, 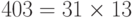 и
и 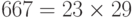 .
. - Определите, являются ли следующие числа Мерсенны простыми числами: М23, М29 и М31. Подсказка: любой делитель числа Мерсенны имеет форму 2kp + 1.
- Приведите некоторые примеры, чтобы показать, что если 2n – 1 — простое число, то n — простое число. Этот факт может использоваться для проверки на простоту? Объясните, как.
- Определите, сколько из следующих целых чисел пройдут испытание Ферма на простоту чисел: 100, 110, 130, 150, 200, 250, 271, 341, 561. Используйте основание 2.
- Определите, сколько из следующих целых чисел пройдут испытание Миллера-Рабина на простоту чисел: 100, 109, 201, 271, 341, 349. Используйте основание 2.
- Используйте рекомендованное испытание, чтобы определить, является ли любое из следующих целых чисел простым числом: 271, 3149, 9673.
- Используйте a = 2, x = 3 и несколько простых чисел, чтобы показать, что если p — простое число, то выполняется следующее сравнение: (x – a) p = (xp – a) (mod p).
- Говорят, что n -ное простое число может быть приближенно вычислено как pn = n ln n. Проверьте это на нескольких простых числах.
- Найдите значение x для следующих наборов сравнений, используя китайскую теорему об остатках.
-
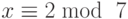 , и
, и 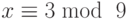
-
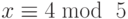 , и
, и 
-
 , и
, и 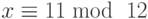
-
- Найдите весь QRs и QNRs в Z13*, Z17* и Z23*.
- Используя квадратичные вычеты, решите следующие сравнения:
- Используя квадратичные вычеты, решите следующие сравнения:
- Найдите результаты приведенных ниже выражений, используя метод "возведения в квадрат и умножения".
- 2124 mod 8
- 32023 mod 461
- 173641 mod 2134
- 200135 mod 2000
- Для группы
 :
:
- Используя свойства дискретных логарифмов, покажите, как решить сравнения:
- Пусть мы имеем компьютер, выполняющий операции со скоростью 1 миллион бит в секунду. Вы хотите затратить только 1 час на испытание простоты чисел. Какое наибольшее число вы можете проверить, используя следующие методы, проверяющие простоту чисел?
- Пусть мы имеем компьютер, выполняющий операции со скоростью 1 миллион бит в секунду. Вы хотите потратить только 1 час на разложение составного целого числа. Какое наибольшее число вы можете разложить на множители, используя следующие методы разложения на множители?
- проверка делением
- Ферма
- Полларда (РО)
- квадратичное решето
- решето поля чисел
- Метод "возведения в квадрат и умножения" — быстрый алгоритм возведения в степень — позволяет нам останавливать программу, если значение основания становится равным 1. Измените алгоритм 13.1, чтобы показать это.
- Перепишите алгоритм 13.1, чтобы проверить биты в порядке от самого старшего к самому младшему.
- Метод "возведения в квадрат и умножения" — быстрый алгоритм возведения в степень — может также быть спроектирован для проверки, является ли число четным или нечетным, вместо того чтобы проверять его разряды. Перепишите алгоритм 13.1, чтобы показать это.
- Напишите алгоритм в псевдокоде для испытания простоты чисел по методу Ферма.
- Напишите алгоритм в псевдокоде для испытания простоты чисел методом извлечения квадратного корня.
- Напишите алгоритм в псевдокоде для китайской теоремы об остатках.
- Напишите алгоритм в псевдокоде, чтобы найти вычет (QR) и невычет (QNR) для любого Zp*.
- Напишите алгоритм в псевдокоде для нахождения первообразного корня для множества Zp*.
- Напишите алгоритм в псевдокоде, чтобы найти все первообразные корни для множества Zp*.
- Напишите алгоритм, чтобы найти и хранить дискретные логарифмы для множества Zp*.


 1(mod p)
1(mod p) (n)
(n)